Neutron Polarimeter

Go Back

Four-vector Algebra

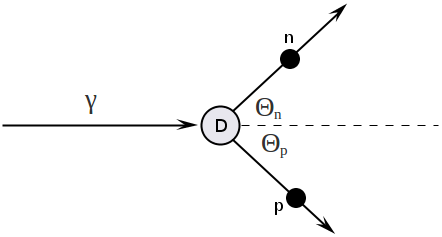
Consider the two bode reaction [math]D(\gamma, n)p[/math]:

Write down all four-vectors:

[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0  \right) [/math] 
[math] p_D     = \left( m_D,\ 0,\ 0,\ 0  \right) [/math] 
[math] p_{n} = \left( E_n,\ \ p_n\cos \Theta_n,\ \ p_n\sin \Theta_n,\ \ 0  \right) [/math] 
[math] p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0  \right) [/math] 

Now apply the conservation of four-momentum:

[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \  p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n[/math]

Squaring both side of equation above and using the four-momentum invariants [math](p^{\mu})^2 = m^2[/math] we have:

[math] m_p^2 = m_D^2 + m_n^2 +  2T_{\gamma}\cdot m_D  - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) [/math]

Detector located at [math]\Theta = 90^o[/math] case

Detector is located at [math]\Theta_n = 90^o[/math], and the formula above is simplified:

[math] m_p^2 = m_D^2 + m_n^2 +  2\ T_{\gamma}\cdot m_D  - 2\ m_D\cdot E_n - 2\ T_{\gamma}E_n [/math]

We can easily solve the equation above with respect to incident photon energy:

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n)}
                  = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D (T_n+m_n)}{2\ (m_D - (T_n+m_n))} [/math]

For non-relativistic neutrons [math]T_n \ll m_n = 939.5\ MeV[/math] and the formula above is become:

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} [/math]

Substituting the corresponding masses, we get finally:

[math]T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1.577\ [MeV]\ \ \ \ [1][/math]

and visa versa:

[math]T_n\ [MeV] = 0.499\cdot T_{\gamma}\ [MeV] - 0.787\ [MeV]\ \ \ \ [2][/math]

Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now:

1) from formula [1] above we can predict the threshold of [math]^2D(n,\gamma)[/math] reaction in [math]\Theta_n = 90^o[/math] direction:

[math]E_{\gamma} = 1.577\ MeV[/math]

2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter).

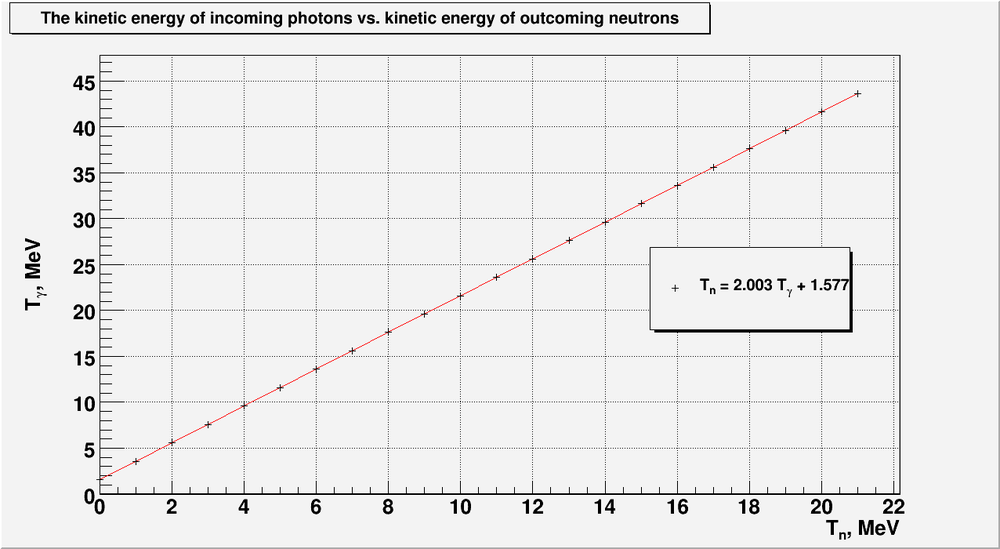
3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy.

 -  for the incident photons up to [math]25\ MeV[/math] we can detect neutrons up to  [math]11.69\ MeV[/math]

 -  for the incident photons up to [math]44\ MeV[/math] we can detect neutrons up to  [math]21.17\ MeV[/math]

4) we can do the error calculations.

Example of error calculation (need to be checked)

example 1

Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:

[math] \delta T_{\gamma} = 2.003\ \delta T_n = 2.003\times 1\ MeV = 2.003\ MeV [/math]

example 2

In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainly of neutrons time of flight.

Say, the neutron's time of flight uncertainty is:

[math]\delta t = 1\ ns[/math]

The neutron kinetic energy is:

[math]T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right][/math]

By taking derivative of the expression above we can find the relative neutron energy error:

[math]\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3} \cdot  \delta t[/math]

Also we need to know the neutron time of flight as function of the neutron energy:

[math]t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} =
         \frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}[/math]

Say, we have 10 MeV neutron, 1.5 m away detector, and neutron's time of flight uncertainty is [math]1\ ns[/math].

Using the formulas above we can find:

[math]t(T_n = 10\ MeV) = 35\ ns[/math]   

[math]\delta T_n(\delta t = 1\ ns) = 0.59\ MeV[/math]

[math]\frac{\delta T_n}{T_n} = \frac{0.59\ MeV}{10\ MeV} = 5.9\ %[/math] 

[math]\delta T_{\gamma} = 2.003\cdot \delta T_n = 2.003\cdot 0.59\ MeV = 1.18\ MeV [/math] 

[math]\frac{\delta T_{\gamma}}{T_{\gamma}} = \frac{1.18\ MeV}{(2.003\cdot 10 + 1.577)\ MeV} = 5.5\ %[/math]

Below are some calculations for different neutron energy based on time flight uncertainty [math]1\ ns[/math]:

[math]\delta t_n[/math]	[math]l[/math]	[math]T_n[/math]	[math]\beta_n[/math]	[math]t_n[/math]	[math]\delta T_n[/math]	[math]\frac{\delta T_n}{T_n}[/math]	[math]\delta T_{\gamma}[/math]	[math]\frac{\delta T_{\gamma}}{T_{\gamma}}[/math]
1 ns	1.5 m	0.1 MeV	0.015	343 ns	0.0006 MeV	0.6 %	0.0012 MeV	0.07 %
1 ns	1.5 m	0.5 MeV	0.033	153 ns	0.006 MeV	1.3 %	0.013 MeV	0.5 %
1 ns	1.5 m	1.0 MeV	0.046	108 ns	0.02 MeV	1.9 %	0.04 MeV	1.0 %
1 ns	1.5 m	2.0 MeV	0.065	77 ns	0.05 MeV	2.6 %	0.11 MeV	1.9 %
1 ns	1.5 m	5.0 MeV	0.103	49 ns	0.21 MeV	4.1 %	0.41 MeV	3.6 %
1 ns	1.5 m	10.0 MeV	0.145	35 ns	0.59 MeV	5.9 %	1.18 MeV	5.5 %
1 ns	1.5 m	20.0 MeV	0.203	25 ns	1.68 MeV	8.4 %	3.36 MeV	8.1 %

Go Back