Neutron Polarimeter

Go Back

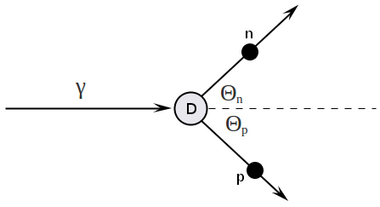
Analysis of energy dependence [math]T_{\gamma}\left( T_n\right)[/math]

four-vectors algebra

[math] E = T + m[/math]
[math] E = p^2 + m^2[/math]

writing four-vectors:

[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0  \right) [/math] 
[math] p_D     = \left( m_D,\ 0,\ 0,\ 0  \right) [/math] 
[math] p_{n} = \left( E_n,\ p_n\cos(\Theta_n),\ p_n\sin(\Theta_n),\ 0  \right) [/math] 
[math] p_{p} = \left( E_p,\ p_p\cos(\Theta_p),\ p_p\sin(\Theta_p),\ 0  \right) [/math] 

Doing four-vector algebra:

[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n \Rightarrow [/math]

[math] p^{\mu\ 2}_p = \left(p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n\right)^2 = 

 p^{\mu\ 2}_{\gamma} + p^{\mu\ 2}_D + p^{\mu\ 2}_n + 

    2\ p^{\mu}_{\gamma}\ p^{\mu}_D - 2\ p^{\mu}_{\gamma}\ p^{\mu}_n - 2\ p^{\mu}_D\ p^{\mu}_n [/math]

[math] m_p^2 - m_{\gamma}^2(=0) - m_D^2 - m_n^2 = [/math]

    [math] = 2\ T_{\gamma}\ m_D - 2\left( T_{\gamma}\ E_n - T_{\gamma}\ p_n\cos(\Theta_n)\right) - 2\ m_D\ E_n  [/math] 

    [math] = 2\ T_{\gamma}\left( m_D - E_n + p_n\cos(\Theta_n) \right) - 2\ m_D\ E_n [/math]

Detector is located at [math]\Theta_n = 90^o[/math], so

[math] T_{\gamma} = \frac {2\ m_D\ E_n + m_p^2 - m_D^2 - m_n^2} {2\left( m_D - E_n \right)} =
                     \frac {2\ m_D\ (T_n + m_n) + m_p^2 - m_D^2 - m_n^2} {2\left( m_D - (T_n + m_n) \right)}[/math]

and visa versa

 [math] T_n = \frac {2\ T_{\gamma}\ m_D + m_D^2 + m_n^2 - m_p^2} {2\left( T_{\gamma} + m_D \right)} - m_n[/math]

how it looks

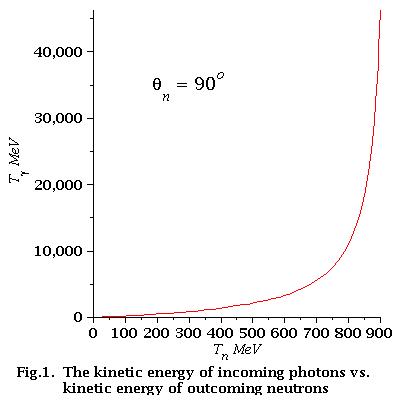
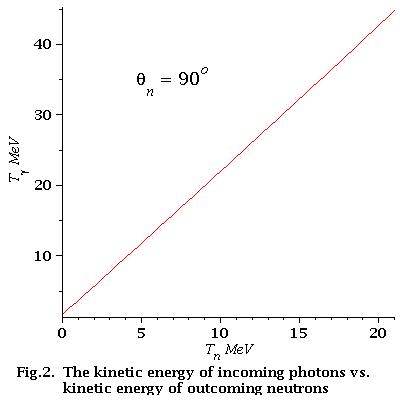
low energy approximation

As we can see from Fig.2 for low energy neutrons (0-21 MeV)

energy dependence of incident photons is linear

Find that dependence. We have:

[math] T_{\gamma}(0\ MeV) = 1.715360792\ MeV [/math]
[math] T_{\gamma}(21\ MeV) = 44.78703086\ MeV [/math]

So, the equation of the line is:

[math] T_{\gamma}
      = \frac{T_{\gamma}(21\ MeV) - T_{\gamma}(0\ MeV)}{21\ MeV - 0\ MeV}\ T_n + T_{\gamma}(0\ MeV) [/math]

Finally for low energy neutrons (0-21 MeV):

[math] T_{\gamma} = 2.051\ T_n + 1.715 [/math]

example of error calculation

example 1

Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:

[math] \delta T_{\gamma} = 2.051\ \delta T_n = 2.051\times 1\ MeV = 2.051\ MeV [/math]

example 2

Say, the neutron's time of flight uncertainly is 1 ns

The neutron's kinetic energy is:

[math]T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right][/math]

And:

[math]\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2 \delta t}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3}[/math]

Also we need the neutron's time of flight as function of neutron's kinetic energy:

[math]t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} =
         \frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}[/math]

Say, we have 10 MeV neutron, 1 m away detector, and neutron's time of flight uncertainty is 1 ns

Using formulas above:

Neutron time of flight:

[math]t(T_n = 10\ MeV) = 23\ ns[/math]   

Neutron kinetic energy errors are:

[math]\delta T_n(\delta t = 1\ ns) = 0.88\ MeV[/math]
[math]\frac{\delta T_n}{T_n} = \frac{0.88\ MeV}{10\ MeV} = 8.8\ %[/math] 

And photon energy errors are:

[math]\delta T_{\gamma} = 2.051\cdot \delta T_n = 2.051\cdot 0.88\ MeV = 1.81\ MeV [/math] 
[math]\frac{\delta T_{\gamma}}{T_{\gamma}} = \frac{1.80\ MeV}{(2.051\cdot 10 + 1.715)\ MeV} = 8.1\ %[/math]

Below are some examples for different detector distance and neutron kinetic energy:

[math]\delta t_n[/math]	[math]l[/math]	[math]T_n[/math]	[math]\beta_n[/math]	[math]t_n[/math]	[math]\delta T_n[/math]	[math]\frac{\delta T_n}{T_n}[/math]	[math]\delta T_{\gamma}[/math]	[math]\frac{\delta T_{\gamma}}{T_{\gamma}}[/math]
1 ns	1 m	5 MeV	0.103	32 ns	0.31 MeV	6.2 %	0.64 MeV	5.3 %
1 ns	1 m	10 MeV	0.145	23 ns	0.88 MeV	8.8 %	1.81 MeV	8.1 %
1 ns	1 m	20 MeV	0.203	16 ns	2.51 MeV	12.6 %	5.16 MeV	12.1 %
1 ns	1 m	0.5 MeV	0.033	102 ns	0.010 MeV	1.9 %
1 ns	1 m	1 MeV	0.046	72 ns	0.028 MeV	2.8 %
1 ns	1 m	2 MeV	0.065	51 ns	0.078 MeV	3.9 %
1 ns	1 m	4 MeV	0.092	36 ns	0.22 MeV	5.5 %

Go Back