Difference between revisions of "Lab 6 TF EIM"
(Created page with 'Lab 6 Pulses and RC Filters Forest_Electronic_Instrumentation_and_Measurement') |
|||
| (26 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Lab 6 Pulses and RC Filters | Lab 6 Pulses and RC Filters | ||
| + | =Differentiator= | ||
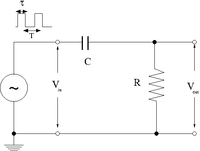
| + | 1.)Construct the circuit below selecting an RC combination such that RC <math>< 10^{-4} </math> s | ||
| + | |||
| + | [[File:TF_EIM_Lab6b.png| 200 px]] | ||
| + | |||
| + | 2.) Adjust the pulse generator to output square pulses which at <math>\tau \approx</math> RC/10. | ||
| + | |||
| + | 3.)Measure<math> V_{in}</math> and <math>V_{out}</math>. Sketch a picture comparing<math> V_{out}</math> and <math>V_{in}</math>. ( 5 pnts.) | ||
| + | |||
| + | 4.) Change the pulse width such that <math>\tau=</math>RC | ||
| + | |||
| + | 5.)Measure<math> V_{in}</math> and <math>V_{out}</math>.Sketch a picture comparing<math> V_{out}</math> and <math>V_{in}</math>.( 5 pnts.) | ||
| + | |||
| + | 6.) Change the pulse width such that <math> \tau</math>=10 RC | ||
| + | |||
| + | 7.)Measure <math>V_{in}</math> and <math>V_{out}</math>.Sketch a picture comparing<math> V_{out}</math> and <math>V_{in}</math>.( 5 pnts.) | ||
| + | |||
| + | |||
| + | ==Questions== | ||
| + | |||
| + | 1.) What happens if the amplitude of <math>V_{in}</math> is doubled.( 5 pnts.) | ||
| + | |||
| + | 2.) What happens if R is doubled and C is halved?( 5 pnts.) | ||
| + | |||
| + | =Integrator= | ||
| + | |||
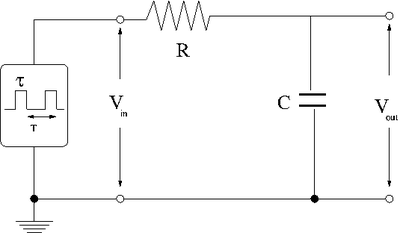
| + | Now repeat the above experiment with the resistor and capacitor swapped to form the low pass circuit below. | ||
| + | |||
| + | [[File:TF_EIM_PulsedRCLowpass.png | 400 px]] | ||
| + | |||
| + | =Pulse Sharpener= | ||
| + | |||
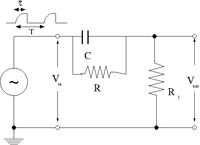
| + | The goal of this section is to demonstrate how well the circuit below can sharpen an input pulse | ||
| + | |||
| + | [[File:TF_EIM_Lab6a.png| 200 px]] | ||
| + | |||
| + | 1.) The first step is to create an input pulse which is rounded, similar to the output of the integrator circuit when RC = 10 <math>\tau</math>. You can do this using a capacitor shorted across the output of the pulse generator. This will essential be coupled to the input impedance of the pulse generator and form a low pass circuit. | ||
| + | |||
| + | As a result the input voltage is given as | ||
| + | |||
| + | :<math>V_{in} = V_0 \left ( 1 - e^{-t/\tau}\right )</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | : <math>\tau=R_{out} C_{out}</math> | ||
| + | :<math>R_{out}</math> = impedance of the function generator at output which produces V_{in} | ||
| + | : <math>C_{out}</math> = capacitor shorting the function generator output to ground (not shown in the above picture) | ||
| + | |||
| + | 2.) The output should be given by | ||
| + | |||
| + | :<math>V_{out} = V_0^{\prime} \left ( 1 - e^{-t/\tau^{\prime}}\right )</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>\tau^{\prime} =\left ( \frac{R_1 R}{R_1+ R}\right )C_1</math> | ||
| + | |||
| + | 3.) Make measurements of the rise time <math>\tau</math> and <math>\tau^{\prime}</math>. The rise time is defined as the time it takes the pulse to go from 0 to <math>(1-e^{-1})</math> = 0.63 of its max value.( 5 pnts.) | ||
| + | |||
| + | 4.) Compare the measurement of <math>\tau^{\prime}</math> to what you expected based on your measured values of <math>C_1</math>, <math>R_1</math> and<math> R</math>.( 15 pnts.) | ||
| + | |||
| + | ==Questions== | ||
| + | |||
| + | 1.) Qualitatify, why is <math>\tau^{\prime} < \tau</math>?( 10 pnts.) | ||
| + | |||
| + | 2.) How is <math>V_{out}</math> worse than <math>V_{in}</math>( 10 pnts.) | ||
[[Forest_Electronic_Instrumentation_and_Measurement]] | [[Forest_Electronic_Instrumentation_and_Measurement]] | ||
Latest revision as of 04:19, 4 March 2011
Lab 6 Pulses and RC Filters
Differentiator
1.)Construct the circuit below selecting an RC combination such that RC s
2.) Adjust the pulse generator to output square pulses which at RC/10.
3.)Measure and . Sketch a picture comparing and . ( 5 pnts.)
4.) Change the pulse width such that RC
5.)Measure and .Sketch a picture comparing and .( 5 pnts.)
6.) Change the pulse width such that =10 RC
7.)Measure and .Sketch a picture comparing and .( 5 pnts.)
Questions
1.) What happens if the amplitude of is doubled.( 5 pnts.)
2.) What happens if R is doubled and C is halved?( 5 pnts.)
Integrator
Now repeat the above experiment with the resistor and capacitor swapped to form the low pass circuit below.
Pulse Sharpener
The goal of this section is to demonstrate how well the circuit below can sharpen an input pulse
1.) The first step is to create an input pulse which is rounded, similar to the output of the integrator circuit when RC = 10 . You can do this using a capacitor shorted across the output of the pulse generator. This will essential be coupled to the input impedance of the pulse generator and form a low pass circuit.
As a result the input voltage is given as
where
- = impedance of the function generator at output which produces V_{in}
- = capacitor shorting the function generator output to ground (not shown in the above picture)
2.) The output should be given by
where
3.) Make measurements of the rise time and . The rise time is defined as the time it takes the pulse to go from 0 to = 0.63 of its max value.( 5 pnts.)
4.) Compare the measurement of to what you expected based on your measured values of , and.( 15 pnts.)
Questions
1.) Qualitatify, why is ?( 10 pnts.)
2.) How is worse than ( 10 pnts.)