Faraday Cup Analysis

Go Back

FC analysis using ADC channel current distribution

For each ADC channel:

[math] ADCSum_{channel}=\sum_{i=1}^{pulses}{ADC_{pulse}^{channel}}[/math]

[math] ADCErr_{channel}=\frac{1}{\sqrt{pulses}}\sum_{i=1}^{pulses}{\sqrt{ADC_{pulse}^{channel}}}[/math]

For distribution over all ADC channel:

[math] ADC^{avg}=\frac{\sum_{i=1}^{16}{ADCSum_{channel}*i}}{\sum_{i=1}^{16}{ADCSum_{channel}}}[/math]

??? [math] ADC^{err}=\frac{\sum_{i=1}^{16}{ADCErr_{channel}*i}}{\sum_{i=1}^{16}{ADCErr_{channel}}}[/math]

FC analysis using pulse by pulse ADC channel mean value distribution

For each beam pulse:

[math] ADC^{avg}_{pulse}=\frac{\sum_{i=1}^{16}{ADC_{i}*i}}{\sum_{i=1}^{16}{ADC_{i}}}[/math]

For distribution over all beam pulses:

[math] ADC^{avg}=\frac{\sum_{i=1}^{pulses}{ADC^{avg}_{pulse}}}{pulses}[/math]

[math] ADC^{err}={ \sqrt{\frac{1}{pulses}\sum_{i=1}^{pulses}{\left(ADC^{avg}_{pulse} - ADC^{avg}\right)^{2}}}}[/math]

Here is:
1. ADC# = bridge#
2. Pulse# = ReadOut# = Entry# = Event#

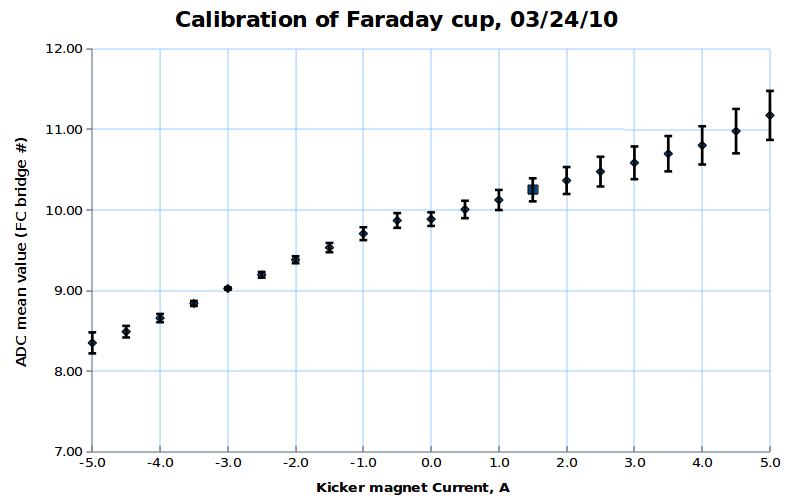
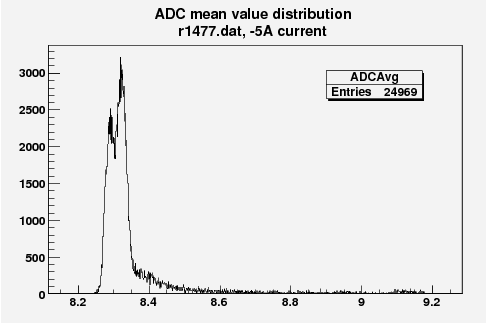
Some examples of ADC mean value distribution. Here are:
1. x axis: ADC mean value for one pulse
2. y axis: number of pulse w/ that ADC mean value

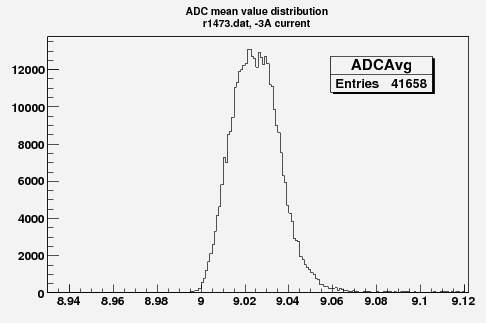
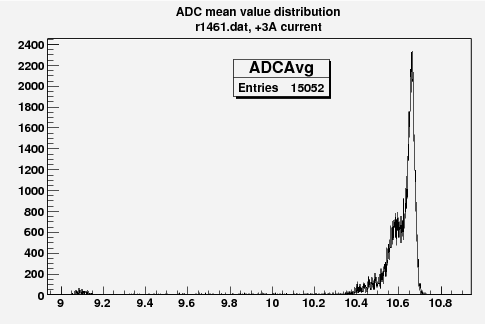
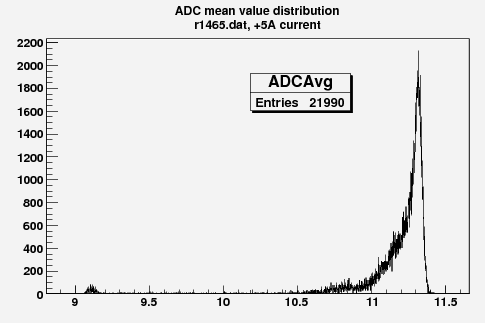
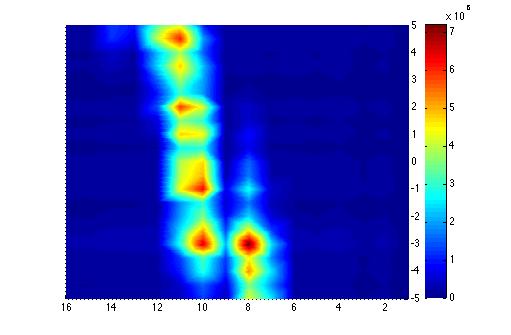
Faraday Cup 3D plot

Below is the plot of the charge in Faraday cup (pC) as a function of magnet current (vertical axis, A) (basically magnetic field) and ADC (horizontal axis).

Faraday Cup "Rain"

Go Up