Difference between revisions of "Trash"
| Line 65: | Line 65: | ||
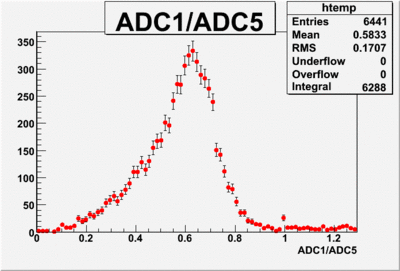
[[Image:Actual_Charge_on_the_strip_and_on_TrigOut_12-12-08.gif|400px]][[Image:ADC1_over_ADC5_r624_12-12-08.gif|400px]]<br> | [[Image:Actual_Charge_on_the_strip_and_on_TrigOut_12-12-08.gif|400px]][[Image:ADC1_over_ADC5_r624_12-12-08.gif|400px]]<br> | ||
| + | |||
| + | ==QCD and asymptotic freedom== | ||
| + | |||
| + | In non-Abelian gauge theories, the beta function can be negative, as first found by [[Frank Wilczek]], [[David Politzer]] and [[David Gross]]. An example of this is the [[beta-function#Examples|beta-function]] for [[Quantum Chromodynamics]] (QCD), and as a result the QCD coupling decreases at high energies. | ||
| + | |||
| + | Furthermore, the coupling decreases logarithmically, a phenomenon known as [[asymptotic freedom]]. The coupling decreases approximately as | ||
| + | ::<math> \alpha_s(k^2) \ \stackrel{\mathrm{def}}{=}\ \frac{g_s^2(k^2)}{4\pi} \approx \frac1{\beta_0\ln(k^2/\Lambda^2)}</math> | ||
| + | where β<sub>0</sub> is a constant computed by Wilczek, Gross and Politzer. | ||
| + | |||
| + | Conversely, the coupling increases with decreasing energy. This means that the coupling becomes large at low energies, and one can no longer rely on Perturbation theory. | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/Coupling_constant] | ||
[[User_talk:Tamar]] | [[User_talk:Tamar]] | ||
Revision as of 06:29, 3 March 2010
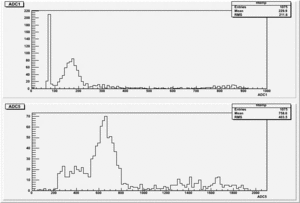
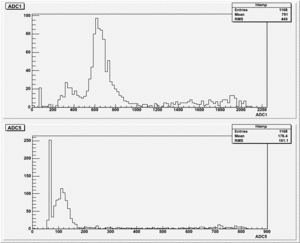
12-12-08
Finding out what is gain for each channel using the Stanford pulse generator.
Setting:
Run Number: r634 && r635
Original pulse from stanford pulse generator goes to the ADC: r636 && r637
I used the attenuator for both channels and it was set to the same value: 12dB = 10.7918.
Gain Calculation
Gain_for_Channel_1 = Gain_TrigOut =
Gain_for_Channel_5 = Gain_Strip =
TrigOut and the stripsignal, both are used as a pulse and go to ADC.
The pulse from the Strips is used as a trigger and gate.
The pulse from the trigout is delayed, Amplified by the Timinig Filter Amplifier(Coarse_Gain=X20, Fine_Gain=8.5 && Integrate=20ns).
Signal from the Strips goes to the Timing Filter Amplifier(Coarse_Gain=X20, Fine_Gain=10.5 && Integrate=20ns). Amplified pulse is devided into two signals, One is sued as a trigger and gate and second as a pulse for ADC. The first one(gate && trigger) is amplified using the Timing Filter Amplifier(Coarse_Gain=X2, Fine_Gain=10 && Integrate=50ns) and used in DIFF. CFD for gate and trigger. Second output from the Amplified strips, goes to delay box(TENNELEC TC 215 DELAY AMPLIFIER) and putted to the ADC.
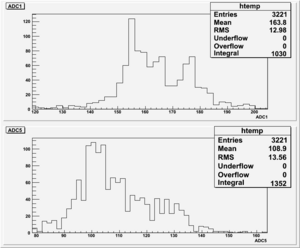
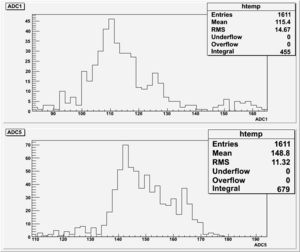
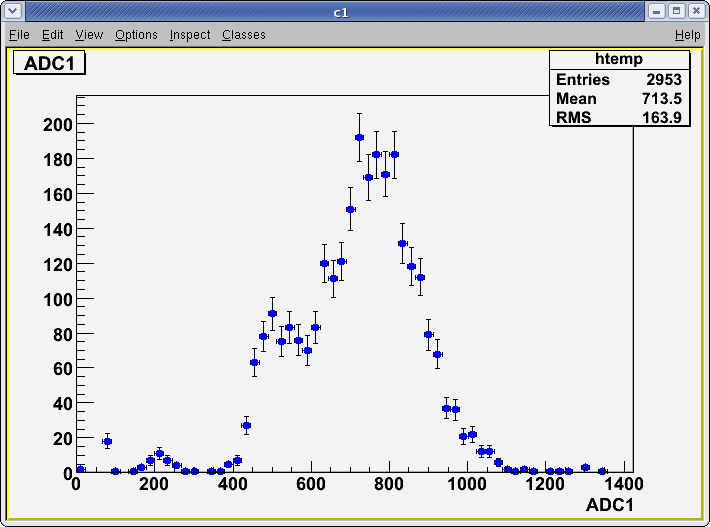
The results shown below are for different Diff. CFD values.
1). Threshold Values: Threshold=1.90, ULD=9.65 && LLD=2.10
Run Number is r613
Start time: Dec 11 16:31:42 End Time: Dec 11 17:32:23
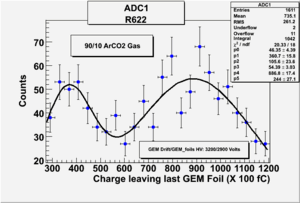
2). Threshold Values: Threshold=3.10, ULD=9.65 && LLD=2.90
Run Number is r622
Start time: Dec 11 19:25:28 End Time: Dec 11 21:53:44
2). Threshold Values: Threshold=3.70, ULD=9.65 && LLD=3.50
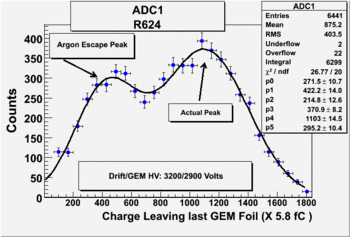
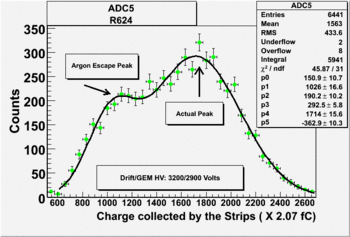
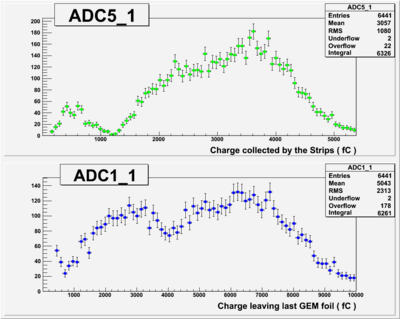
Run Number is r624
Start time: Dec 11 21:58:37 End Time: Dec 12 12:19:53
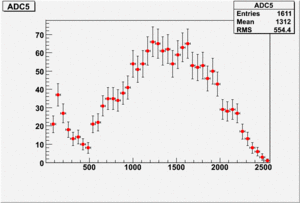
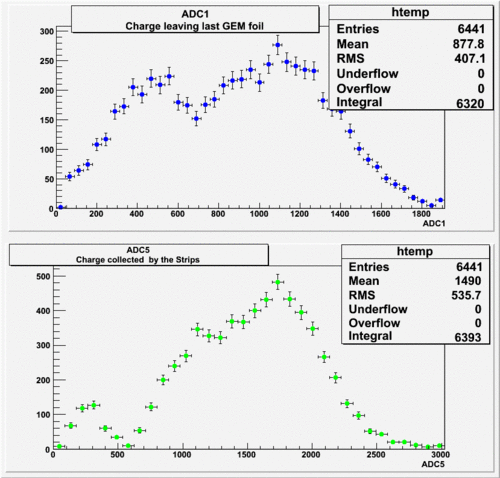
The result shown below is reasonable. The charge that left the last GEM foil is greater than the charge collected by the strips.
QCD and asymptotic freedom
In non-Abelian gauge theories, the beta function can be negative, as first found by Frank Wilczek, David Politzer and David Gross. An example of this is the beta-function for Quantum Chromodynamics (QCD), and as a result the QCD coupling decreases at high energies.
Furthermore, the coupling decreases logarithmically, a phenomenon known as asymptotic freedom. The coupling decreases approximately as
where β0 is a constant computed by Wilczek, Gross and Politzer.
Conversely, the coupling increases with decreasing energy. This means that the coupling becomes large at low energies, and one can no longer rely on Perturbation theory.