Difference between revisions of "Forest FermiGoldenRule Notes"
| (98 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Fermi's Golden Rule= | =Fermi's Golden Rule= | ||
| − | Fermi's Golden rule is used to calculate the probability (per unit time) of a quantum mechanical transition between two quantum | + | Fermi's Golden rule is used to calculate the probability (per unit time) of a quantum mechanical transition between two particles ( a and b) in an initial quantum state <math>i</math> to two particles ( c and d) in a final state <math>f</math>. |
| − | + | : a + b <math>\rightarrow</math> c + d | |
| + | where a is the incoming particle and b is the target particle. | ||
| + | |||
| + | Although Fermi first coined the term "Golden Rule", Dirac developed most of the machinery. | ||
| + | |||
| + | Let <math>\Phi</math> represent the Flux of particle per unit time through a unit area normal to the beam. Then | ||
| + | |||
| + | : <math>\Phi = n_a v_i </math> | ||
| + | where | ||
| + | |||
| + | :<math>n_a</math> = density of particles in the incident beam | ||
| + | :<math>v_i</math> = velocity of a relative to b. | ||
| + | |||
| + | The probability the incident particle will hit a target particle is given by the cross-section <math>\sigma</math> times the number of target particles per unit area <math>(n_b)</math>. | ||
| + | |||
| + | The number of interactions therefor will be given by | ||
| + | |||
| + | : Number of Interactions per unit area per unit second= <math>n_b \sigma \times \Phi | ||
| + | </math> | ||
| + | |||
| + | The transition rate <math>(W)</math> per target particle <math>(n_b)</math> is | ||
| + | |||
| + | : <math>\frac{W}{n_b} = \sigma \Phi = \sigma n_a v_i</math> | ||
| + | |||
| + | Solving the above for the Cross section \sigma we have | ||
| + | |||
| + | : <math>\sigma = \frac{W}{n_b \Phi}= \frac{W}{n_b n_a v_i}</math> | ||
| + | |||
| + | A calculation of the transition rate W si equivalent to calculating the cross section of the scattering process. | ||
| + | |||
| + | Fermi's Golden rule says that the transition rate <math>W</math> is given by a transition matrix element (or "Amplitude") <math>M_{i,f}</math> weighted by the phase space and Plank's constant <math>\hbar</math> such that | ||
| + | |||
| + | : <math>W = \frac{2 \pi}{\hbar} |M_{i,f}|^2 \times </math>(Phase Space) = \frac{0.693}{t_{1/2}} | ||
| + | |||
| + | :<math>t_{1/2} =</math> transition half life. | ||
==Transition Amplitude== | ==Transition Amplitude== | ||
| − | :<math>| M_{i,f}| ^2 \equiv \int \ | + | :<math>| M_{i,f}| ^2 \equiv \int \psi_f^{*}(\vec{r}) H_{int} \psi_i(\vec{r}) dr^3</math> |
where | where | ||
| Line 17: | Line 51: | ||
The off diagonal elements of the <math>M_{i,f}</math> matrix tell you the transition probablility. | The off diagonal elements of the <math>M_{i,f}</math> matrix tell you the transition probablility. | ||
| + | |||
| + | |||
| + | ===Stationary State=== | ||
| + | |||
| + | The stationary state system is given by the solutions of the schrodinger equation for H_0 | ||
| + | |||
| + | : <math>i \hbar \frac{\partial \psi_i}{\partial t} = H_0 \psi_i</math> | ||
| + | : <math>\psi_i = u_n e^{-\frac{i E_n}{\hbar}t}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>H_0 u_n = E_n u_n</math> | ||
| + | :<math>E_n</math> = energy eigen values | ||
| + | |||
| + | ===Interaction Hamiltonian === | ||
| + | |||
| + | |||
| + | :<math>H_{int}</math> = Interaction Hamiltonian = perturbation to <math>H_0</math> which causes a transition/interaction. The time dependent schrodinger equation for this perturbation is: | ||
| + | |||
| + | : <math>i \hbar \frac{\partial \psi}{\partial t} = (H_0 + H_{int} ) \psi</math> | ||
| + | |||
| + | |||
| + | One can write the solution <math>\psi</math> in terms of a linear combination of the basis functions <math>(u_n)</math> from the Stationary State solution. | ||
| + | |||
| + | : <math>\psi = \sum_n a_n(t) u_n(x) e^{- \frac{i E_n}{\hbar}t}</math> | ||
| + | |||
| + | You jsut need to find the components of the basis eigenfunctions (eigenvectors) using the Schrodinger equation | ||
| + | |||
| + | :<math>i \hbar \sum_n \frac{d a_n}{dt} u_n e^{- \frac{i E_n}{\hbar}t} + \sum E_n a_n u_n e^{- \frac{i E_n}{\hbar}t} = \sum_n a_n (H_0 + H_{int}) u_n e^{- \frac{i E_n}{\hbar}t}</math> | ||
| + | |||
| + | Because | ||
| + | : <math>H_0 u_n = E_n u_n</math> | ||
| + | |||
| + | The second term on the left hand side is canceled with the <math>H_0</math> term on the right hand side | ||
| + | |||
| + | :<math>i \hbar \sum_n \frac{d a_n}{dt} u_n e^{- \frac{i E_n}{\hbar}t} = \sum_n a_n H_{int} u_n e^{- \frac{i E_n}{\hbar}t}</math> | ||
| + | |||
| + | multiple both sides by <math>u_{n^{\prime}}^* e^{i\frac{E_{n^{\prime}}}{\hbar}t}</math> and integrate over the whole volume | ||
| + | |||
| + | |||
| + | :<math> i \hbar \frac{d a_n}{dt} \delta_{n n^{\prime}}= \sum_n < u_{n^{\prime}} | H_{int} | u_n> a_n e^{- i\frac{E_{n^{\prime}}-E_n}{\hbar}t}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | : <math>< u_{n^{\prime}} | H_{int} | u_n> = \int d^3x u_{n^{\prime}}^* H_{int} u_n</math> | ||
| + | |||
| + | Integrate the above equation | ||
| + | |||
| + | :<math>\int_0^T \frac{d a_{n^{\prime}}}{dt} = \frac{-i}{\hbar} \int_0^T \sum_n < u_{n^{\prime}} | H_{int} | u_n> a_n e^{i\frac{E_{n^{\prime}}-E_n}{\hbar}t} dt</math> | ||
| + | |||
| + | If we make the following assumptions | ||
| + | |||
| + | 1.) The quantum state is <math>u_{\alpha}</math> just before the particle interacts via <math>H_{int}</math><math>\Rightarrow u_n = u_{\alpha}</math> | ||
| + | |||
| + | 2.) <math>H_{int}</math> acts over a very small time ( strong force range is <math>10^{-15} m</math>) | ||
| + | |||
| + | 3.) <math>H_{int}</math> is so weak that the initial quantum state is not substantially altered by the interaction. Or other states are very weakly involved (<math>H_{int}</math> prefers one state over all the others) | ||
| + | |||
| + | : <math>a_n=\left \{ {1 \;\;\;\; n= \alpha \atop 0 \;\;\;\; n \ne \alpha} \right .</math> | ||
| + | = 1 | ||
| + | |||
| + | Then | ||
| + | |||
| + | : <math>\sum_n < u_{n^{\prime}} | H_{int} | u_n> = < u_{n^{\prime}} | H_{int} | u_{\alpha}></math> | ||
| + | |||
| + | |||
| + | :<math>\Rightarrow a_{n^{\prime}} = \frac{-i}{\hbar} \int_0^T < u_{n^{\prime}} | H_{int} | u_{\alpha}> (1) e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t} dt</math> | ||
| + | : <math>= \frac{-i}{\hbar} < u_{n^{\prime}} | H_{int} | u_{\alpha}> \int_0^T e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t} dt</math> | ||
| + | : <math>= \frac{-i}{\hbar} < u_{n^{\prime}} | H_{int} | u_{\alpha}> \frac{\hbar}{i(E_{n^{\prime}}-E_{\alpha})}e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t}|_0^T | ||
| + | </math> | ||
| + | : <math>= -\frac{< u_{n^{\prime}} | H_{int} | u_{\alpha}>}{(E_{n^{\prime}}-E_{\alpha})}\left ( e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T} -1\right ) | ||
| + | </math> | ||
| + | |||
| + | :<math>a_{n^{\prime}} =\frac{< u_{n^{\prime}} | H_{int} | u_{\alpha}>}{(E_{n^{\prime}}-E_{\alpha})}\left ( 1 - e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right )</math> = amplitude for making a transition from <math>u_{\alpha}</math> to <math>u_{n^{\prime}}</math> | ||
| + | |||
| + | ===Transition Probability=== | ||
| + | |||
| + | The probability <math>(P_{n^{\prime} \alpha} )</math> of making a transition from t state <math>u_{\alpha}</math> to the state <math>u_{n^{\prime}}</math> is given by the magnitude of the amplitude <math>a_{n^{\prime}}</math> | ||
| + | |||
| + | : <math>P_{n^{\prime} \alpha}= | a_{n^{\prime}} |^2</math> | ||
| + | : <math>= \frac{|< u_{n^{\prime}} | H_{int} | u_{\alpha}>|^2}{(E_{n^{\prime}}-E_{\alpha})^2}\left ( 1 - e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right ) \left ( 1 - e^{-i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right ) | ||
| + | </math> | ||
| + | :<math>= \frac{|< u_{n^{\prime}} | H_{int} | u_{\alpha}>|^2}{(E_{n^{\prime}}-E_{\alpha})^2} 4 \sin^2 \left(\frac{E_{n^{\prime}}-E_{\alpha}}{2\hbar}T \right )</math> | ||
| + | |||
| + | : <math>e^{\pm ix} = \cos(x) \pm i \sin(x)</math> and <math>\cos(\theta) = 1 - 2 \sin^2(\theta/2)</math> | ||
| + | |||
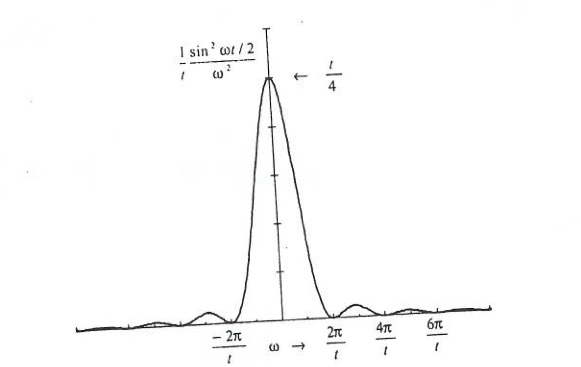
| + | What does this probability function look like? | ||
| + | |||
| + | |||
| + | [[Image:FermiGoldenRule_SineSqr.jpg]] | ||
| + | |||
| + | ;Notice | ||
| + | : The probability of a transition gets smaller if the energy difference between the state <math>( E_{n^{\prime}}-E_{\alpha})</math> gets bigger. | ||
| + | :It illustrates the uncertainty principle <math>\Delta E \Delta t > \hbar</math>. <math>\Delta w</math> is the Half Width of the peak. In the above picture <math>\Delta w t \approx \pi</math>. | ||
| + | :Another indication of the uncertainty principle is oberved if you let <math>t \rightarrow \infty</math> then above function goes to a delta function <math>(\frac{\pi}{2}\delta(w))</math> | ||
| + | :For <math>\Delta E \equiv \frac{2 \pi \hbar}{T}</math> Most of the above function lies in the interval <math>[(E_{\alpha} - \Delta E ),(E_{\alpha} + \Delta E )]</math> | ||
| + | |||
| + | The probability of transition (The total transition probability to all states) is given by adding up all the probabilities to individual states. | ||
| + | |||
| + | : <math>P = \sum_{n^{\prime}} P_{n^{\prime} \alpha}</math> | ||
| + | : <math>= 4 \sum_{n^{\prime}} \frac{|< u_{n^{\prime}} | H_{int} | u_{\alpha}>|^2}{(E_{n^{\prime}}-E_{\alpha})^2} \sin^2 \left(\frac{E_{n^{\prime}}-E_{\alpha}}{2\hbar}T \right )</math> | ||
| + | |||
| + | If we assume the states are all clustered together as in a continuum then | ||
| + | |||
| + | :<math>|< u_{n^{\prime}} | H_{int} | u_{\alpha}>|^2 =</math> constant <math>\equiv |< \beta | H_{int} | \alpha>|^2</math> | ||
| + | |||
| + | This assumption isn't so bad when you realize that since the above function lies over a finite energy interval and that that finite energy interval contains similar states. | ||
| + | |||
| + | Since we assume a continuum the summation becomes an integral such that | ||
| + | :<math>P(T) = 4 |< \beta | H_{int} | \alpha>|^2 \int \frac{\sin^2 \left(\frac{E(N)-E_{\alpha}}{2\hbar}T \right )}{(E(N)-E_{\alpha})^2} dN</math> | ||
| + | |||
| + | Where the Energy <math>(E)</math> is an explicit function of state number <math>N</math>. | ||
| + | |||
| + | Using the chain rule we can recast the integral | ||
| + | |||
| + | let | ||
| + | :<math>x \equiv \frac{(E(N)-E_{\alpha})T}{2\hbar}</math> | ||
| + | |||
| + | Then | ||
| + | |||
| + | : <math>dx = \frac{T}{2 \hbar} dE(N)</math> | ||
| + | |||
| + | and | ||
| + | |||
| + | : <math>dN = \frac{dN}{dE} dE = \frac{dN}{dE} \frac{2 \hbar}{T} dx</math> | ||
| + | |||
| + | :<math>P(T) = 4 |< \beta | H_{int} | \alpha>|^2 \frac{dN}{dE} \frac{T}{2 \hbar} \int_{-\infty}^{\infty} \frac{\sin^2 (x)}{(x)^2} dx</math> | ||
| + | |||
| + | :<math>\int_{-\infty}^{\infty} \frac{\sin^2 (x)}{(x)^2} dx = \pi</math> | ||
| + | |||
| + | |||
| + | :<math>P(T) = \frac{2 \pi T}{ \hbar}|< \beta | H_{int} | \alpha>|^2 \frac{dN}{dE} </math> | ||
| + | |||
| + | |||
| + | :<math>P|< \beta | H_{int} | \alpha>|^2 </math> =:<math>| M_{i,f}| ^2 \equiv \int \psi_f^{*}(\vec{r}) H_{int} \psi_i(\vec{r}) dr^3</math> | ||
| + | |||
| + | :<math>\frac{dN}{dE} = </math> Density of states<math> ( \rho(\alpha))</math> | ||
==Single Particle decay== | ==Single Particle decay== | ||
| Line 47: | Line 218: | ||
;<math>S = \frac{1}{2!} = \frac{1}{1 \cdot 2} = \frac{1}{2}</math> | ;<math>S = \frac{1}{2!} = \frac{1}{1 \cdot 2} = \frac{1}{2}</math> | ||
| − | Since the pion is initially at rest (or we can go to its rest | + | Since the pion is initially at rest (or we can go to its rest frame and then Lorentz boost back to the lab frame) |
;<math>p_1^\mu = (E_1,p_1) = (E_1,0) = (m_{\pi^0},0)</math> | ;<math>p_1^\mu = (E_1,p_1) = (E_1,0) = (m_{\pi^0},0)</math> | ||
| Line 86: | Line 257: | ||
; Caveat | ; Caveat | ||
| − | : | + | : Sometimes <math>|M|</math> will depend on the momentum vector directions in which case the integral must be done after evaluating the matrix element amplitude. An example of this is when the transition is spin dependent <math>(\vec{p} \cdot \vec{s})</math> as in the hyperfine interaction or polarization based transitions. |
=== Example: Two -Body decay (fission fragments) === | === Example: Two -Body decay (fission fragments) === | ||
| − | Now consider a more general case in | + | Now consider a more general case in which the decay daughters have mass: |
:<math>d \Gamma = \hbar W = | M |^2 \frac{S}{2 \hbar m_1} \left [ \left ( \frac{d^3\vec{p}_2}{(2 \pi)^3 2E_2} \right )\left ( \frac{d^3\vec{p}_3}{(2 \pi)^3 2E_3} \right ) \right ] (2 \pi)^4 \delta^4(p_1^\mu-p_2^\mu-p_3^\mu)</math> | :<math>d \Gamma = \hbar W = | M |^2 \frac{S}{2 \hbar m_1} \left [ \left ( \frac{d^3\vec{p}_2}{(2 \pi)^3 2E_2} \right )\left ( \frac{d^3\vec{p}_3}{(2 \pi)^3 2E_3} \right ) \right ] (2 \pi)^4 \delta^4(p_1^\mu-p_2^\mu-p_3^\mu)</math> | ||
| Line 161: | Line 332: | ||
| − | The general expression for the cross section via Fermi's golden rule is given as | + | The general expression for the cross section via Fermi's golden rule is similar to the above pion decay example if you consider m_1 and m_2 forming an intermediate state and is given as |
: <math>d^2 \sigma = \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{\sqrt{ \left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2 - (m_1 m_2)^2}} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{E_4}\right) \right ] \delta^4(p_1^{\mu}+p_2^{\mu}-p_3^{\mu}-p_4^{\mu})</math> | : <math>d^2 \sigma = \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{\sqrt{ \left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2 - (m_1 m_2)^2}} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{E_4}\right) \right ] \delta^4(p_1^{\mu}+p_2^{\mu}-p_3^{\mu}-p_4^{\mu})</math> | ||
| Line 207: | Line 378: | ||
: <math>\frac{ d \sigma}{d \Omega}=\int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{p_3^2 d p_3}{E_3}\right) \left ( \frac{1}{\sqrt{p_3^2 + m_4^2}}\right) \right ] \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2}) </math> | : <math>\frac{ d \sigma}{d \Omega}=\int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{p_3^2 d p_3}{E_3}\right) \left ( \frac{1}{\sqrt{p_3^2 + m_4^2}}\right) \right ] \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2}) </math> | ||
| − | : <math>=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)p_1} \int | + | : <math>=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)p_1} \int \frac{|M|^2 p_3^2 }{E_3\sqrt{p_3^2 + m_4^2}} \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2})d p_3 </math> |
| + | |||
| + | This integral looks just like the 2-Body decay problem if you let <math>m_1 = E_1 + E_2</math> | ||
| + | |||
| + | :<math>\frac{ d \sigma}{d \Omega}=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)p_1} \frac{|M|^2 p_3 }{E_1+E_2}</math> | ||
| + | :<math>=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)^2} \frac{|M|^2 p_3 }{p_1}</math> | ||
| + | :<math>=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S|M|^2}{(E_1 + E_2)^2} \frac{ p_3 }{p_1}</math> | ||
| + | |||
| + | Note: In Center of Momentum frame <math>|\vec{p}_1| = |\vec{p}_2|</math> and <math>|\vec{p}_3| =|\vec{p}_4|</math> | ||
| + | |||
| + | so | ||
| + | |||
| + | :<math>\frac{ d \sigma}{d \Omega} \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S|M|^2}{(E_1 + E_2)^2} \frac{ p_f }{p_i}</math> | ||
| + | |||
| + | where <math>p_f = |\vec{p}_3| = |\vec{p}_4|</math> and <math>p_i = |\vec{p}_1| = |\vec{p}_2|</math> | ||
| + | |||
| + | ;Units | ||
| + | : Notice that the number of integrals is equal to the number of particles in the interaction. The units of <math>|M|^2</math> change with the number of integrals <math>(n)</math> such that <math>[|M|^2] = \left (\frac{MeV}{c}\right)^{4-n}</math> | ||
| − | [http://iac.isu.edu | + | [http://wiki.iac.isu.edu/index.php/Classes Back to Classes] [[Classes]] |
Latest revision as of 21:14, 26 April 2009
Fermi's Golden Rule
Fermi's Golden rule is used to calculate the probability (per unit time) of a quantum mechanical transition between two particles ( a and b) in an initial quantum state to two particles ( c and d) in a final state .
- a + b c + d
where a is the incoming particle and b is the target particle.
Although Fermi first coined the term "Golden Rule", Dirac developed most of the machinery.
Let represent the Flux of particle per unit time through a unit area normal to the beam. Then
where
- = density of particles in the incident beam
- = velocity of a relative to b.
The probability the incident particle will hit a target particle is given by the cross-section times the number of target particles per unit area .
The number of interactions therefor will be given by
- Number of Interactions per unit area per unit second=
The transition rate per target particle is
Solving the above for the Cross section \sigma we have
A calculation of the transition rate W si equivalent to calculating the cross section of the scattering process.
Fermi's Golden rule says that the transition rate is given by a transition matrix element (or "Amplitude") weighted by the phase space and Plank's constant such that
- (Phase Space) = \frac{0.693}{t_{1/2}}
- transition half life.
Transition Amplitude
where
- = initial quantum state of the system which is an eigenstate of the time independent ("steady state") Hamiltonian ()
- = final quantum state of system after a transition
- = the part of the total Hamiltonian () which describes the interaction responsible for the transition.
- = Unperturbed ("steady state") Hamiltonian
- = total Hamiltonian describing the quantum mechanical system
- integration over all space
The off diagonal elements of the matrix tell you the transition probablility.
Stationary State
The stationary state system is given by the solutions of the schrodinger equation for H_0
where
- = energy eigen values
Interaction Hamiltonian
- = Interaction Hamiltonian = perturbation to which causes a transition/interaction. The time dependent schrodinger equation for this perturbation is:
One can write the solution in terms of a linear combination of the basis functions from the Stationary State solution.
You jsut need to find the components of the basis eigenfunctions (eigenvectors) using the Schrodinger equation
Because
The second term on the left hand side is canceled with the term on the right hand side
multiple both sides by and integrate over the whole volume
where
Integrate the above equation
If we make the following assumptions
1.) The quantum state is just before the particle interacts via
2.) acts over a very small time ( strong force range is )
3.) is so weak that the initial quantum state is not substantially altered by the interaction. Or other states are very weakly involved ( prefers one state over all the others)
= 1
Then
- = amplitude for making a transition from to
Transition Probability
The probability of making a transition from t state to the state is given by the magnitude of the amplitude
- and
What does this probability function look like?
- Notice
- The probability of a transition gets smaller if the energy difference between the state gets bigger.
- It illustrates the uncertainty principle . is the Half Width of the peak. In the above picture .
- Another indication of the uncertainty principle is oberved if you let then above function goes to a delta function
- For Most of the above function lies in the interval
The probability of transition (The total transition probability to all states) is given by adding up all the probabilities to individual states.
If we assume the states are all clustered together as in a continuum then
- constant
This assumption isn't so bad when you realize that since the above function lies over a finite energy interval and that that finite energy interval contains similar states.
Since we assume a continuum the summation becomes an integral such that
Where the Energy is an explicit function of state number .
Using the chain rule we can recast the integral
let
Then
and
- =:
- Density of states
Single Particle decay
Consider the case when a single particle decays into multiple fragments (several other particles)
where
- = probability per second that the particle will decay
- = a symmetry factor of for every group of identical particles in the final state
- = 4-momentum of the particle. ;
- = conservation of 4-momentum
- Note
- = invariant under Lorentz transformations
Example: Pi-zero () decay
we are interested in calculating
Consider the decay of a neutral pion () into two photons ().
The two gammas are identical particles so
Since the pion is initially at rest (or we can go to its rest frame and then Lorentz boost back to the lab frame)
Because photons have no mass, :
Integrating over :
If ( the transition does not depend on the momentum vector directions)
then
- with the additional conditions that and which must be applied when evaluating
- Units check
- = energy eigenvalues squared
- transition probability per unit time
- Caveat
- Sometimes will depend on the momentum vector directions in which case the integral must be done after evaluating the matrix element amplitude. An example of this is when the transition is spin dependent as in the hyperfine interaction or polarization based transitions.
Example: Two -Body decay (fission fragments)
Now consider a more general case in which the decay daughters have mass:
We don't know if the two daughter particles are identical so leave as a funtion.
We can still do the calculation in the mother particles rest frame.
Now that the daughters have mass we need:
Recast the delta function:
Upon integrating over
After integrating over the delta function gives you
Once again , if the transition amplitude does not depend on the vector directions of and then you can integrate over angles and get a .
Let
Then
substituting
where
and
= momentum when
or
2 Body scattering in CM frame
Lets consider the case when two particles ( and ) collide and are transformed into two separate particle ( and ). An interaction happens during the collision which changes the two particles into two other particles.
Calculate the differential cross section, in the center of momentum frame, assuming that is the amplitude for this collision.
The general expression for the cross section via Fermi's golden rule is similar to the above pion decay example if you consider m_1 and m_2 forming an intermediate state and is given as
In the CM frame
or
substituting the above and
- :
into the cross ection equation we have
integrating over we have
Unfortunately depends on scattering angles. For some interactions it even depends on angles (5th structure function, single spin asymmetries).
If you write the cross section in terms of a differential cross section in solid angle then only the momentum part of the integral remains.
This integral looks just like the 2-Body decay problem if you let
Note: In Center of Momentum frame and
so
where and
- Units
- Notice that the number of integrals is equal to the number of particles in the interaction. The units of change with the number of integrals such that