|
|
| Line 142: |
Line 142: |
| | :<math>P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}</math> | | :<math>P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}</math> |
| | | | |
| − | Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles which perpendicular to the Z-axis (transverse components:<math>\vec{p}_{1,\perp}</math> and <math>\vec{p}_{1,\perp}</math>) are equal and opposite by conservation of momentum. | + | Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles which perpendicular to the Z-axis (transverse components:<math>\vec{p}_{1,\perp}</math> and <math>\vec{p}_{2,\perp}</math>) are equal and opposite by conservation of momentum. |
| | + | |
| | + | :<math>\vec{p}_{\perp}\equiv -\vec{p}_{2,\perp}</math> |
Revision as of 02:11, 31 October 2007
Lorentz Transformations
The picture below represents the relative orientation of two different coordinate systems [math](S, S^{\prime})[/math] . [math]S[/math] is at rest (Lab Frame) and [math]S^{\prime}[/math] is moving at a velocity v to the right with respect to frame [math]S[/math].
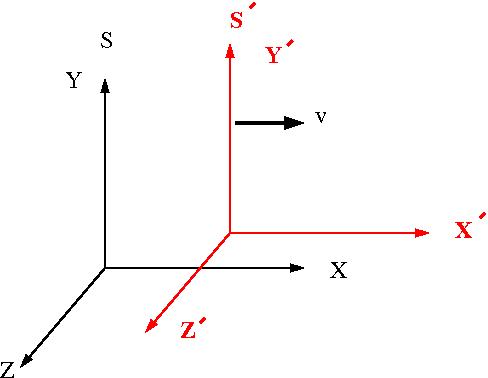
The relationship between the coordinate[math] (x,y,z,ct)[/math] of an object in frame [math]S[/math] to the same object described using the coordinates [math](x^{\prime},y^{\prime},z^{\prime},ct^{\prime})[/math] in frame [math]S^{\prime}[/math] is geven by the Lorentz transformation:
4- vector notation
The 4-vector notation is given as
- [math]x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}[/math]
where
- [math] x^0 \equiv ct[/math]
- [math]x^1 \equiv x[/math]
- [math]x^2\equiv y[/math]
- [math]x^3\equiv z[/math]
- [math]\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ][/math]
- [math]\beta = \frac{v}{c} = \frac{pc}{E}[/math]
- [math]\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}[/math]
- NOTE
- It is common in particle physics to define [math] c \equiv 1[/math] making [math]\gamma = \frac{E}{m}[/math] where [math]m[/math] is in units of [math]\frac{\mbox{MeV}}{\mbox{c}^2}[/math]
- example
- [math]x^{0^{\prime}} = \sum_{\nu=0}^2 \Lambda_{\nu}^0 x^{\nu} = \Lambda_0^0 x^0 + \Lambda_1^0 x^1 \Lambda_2^0 x^2 + \Lambda_3^0 x^2[/math]
- [math]ct^{\prime}= \gamma x^0 - \gamma \beta x^1 + 0 x^2 + 0 x^3 = \gamma ct - \gamma \beta x = \gamma(ct -\beta x)[/math]
- Or in matrix form the tranformation looks like
- [math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]
- Note
- Einstein's summation convention drops the [math]\sum[/math] symbols and assumes it to exist whenever there is a repeated subscript and uperscript
- ie; [math]x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}[/math]
- in the example above the[math] \nu[/math] symbol is repeated thereby indicating a summation over [math]\nu[/math].
Momentum 4-vector
- [math]p^{\mu} \equiv (\frac{E}{c} , \vec{p})[/math]
- [math]p_{\mu} \equiv (\frac{E}{c} , -\vec{p})[/math]
- [math]p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2[/math]
- Note
- There is another convention used for 4-vector notation by Perkins and Koller which goes like this
- [math]p^{\mu} \equiv (\vec{p},iE)[/math]
- [math]p_{\mu} \equiv (\vec{p},iE)[/math]
Trig Method
Another way to represent the lorentz transformation is by using the substitution
- [math]\sin (\alpha) \equiv \beta \equiv \frac{v}{c}[/math]
- [math]\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}[/math]
- The Matrix form pf the tranformation looks like
- [math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]
- Or the reverse transformation
- [math]\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )[/math]
- Notice that you just needed to change the signs for the inverse matrix [math]\Lambda^{-1}[/math]
Proper Time and Length
Proper Time
- Proper Time [math]\Tau[/math]
- The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).
The time given in any frame (t) = [math]\gamma \Tau[/math]
- Note
- since [math]\gamma \gt 1[/math] you expect the Proper time interval to be the smallest
Proper Length
- Proper Length[math] (c\Tau)[/math]
- The length of an object in the object's rest frame.
Invariant Length
Transformation Examples
Decay of Particle to 2 Bodies
Consider the decay of the [math]\rho_0[/math] meson at rest into two pions ([math]\pi^+[/math] and [math]\pi^-[/math] )
File:NeutralRhoMesonDecayDiagram.jpg
The diagram above shows a [math]\rho_0[/math] meson at rest in the lab which then decays into two pions of momentum [math]p_1[/math] and [math]p_2[/math] in the center of momentum frame of the [math]\rho_0[/math] meson.
If [math]P^{\mu}[/math] represent the total momentum of the system before the decay then
- [math]P^{\mu} = (E,0) =(M,0) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}[/math]
- [math]\Rightarrow 0 = \vec{p}_1 + \vec{p}_2[/math]
or
- [math]\vec{p}_1 = - \vec{p}_2[/math]
Let
- [math]p \equiv |\vec{p}_1 | = |\vec{p}_2 |[/math]
Conservation of Energy
- [math]\Rightarrow E_{tot} = M = E_1 + E_2 = \sqrt{m_1^2 + p^2} + \sqrt{m_2^2 + p^2}[/math]
solving for p
- [math]\Rightarrow p = \frac{1}{2M} \sqrt{[M^2 - (m_1-m_2)^2][M^2-(m_1+m_2)^2]}[/math]
- [math]\Rightarrow M \ge m_1 + m_2[/math] is required to avoid the unphysical condition that the momentum of the particles after a decay would be an imaginary number
Using
- [math]p \equiv |\vec{p}_1 | = |\vec{p}_2 |[/math]
- [math]E_1^2 - m_1^2 = E_2^2 - m_2^2[/math]
- [math]\Rightarrow E_2 = \sqrt{E_1^2 - m_1^2 + m_2^2}[/math]
Combine this with the conservation of energy equation above:
- [math] E_1 + E_2 = E_1 + \sqrt{E_1^2 - m_1^2 + m_2^2} = M[/math]
- [math]\Rightarrow E_1 - M = \sqrt{E_1^2 - m_1^2 + m_2^2}[/math]
Square both sides of the above equation
- [math]E_1^2 -2ME_1 + M^2 = E_1^2- m_1^2 + m_2^2[/math]
- [math]\Rightarrow E_1 = \frac{M^2+m_1^2-m_2^2}{2M}[/math]
Similarly
- [math] E_2 = \frac{M^2+m_2^2-m^2_1}{2M}[/math]
- Note
- [math]\vec{p}_1 = -\vec{p}_2[/math]
- [math]\Rightarrow[/math] The daughter particles (pions) from the decay of the Mother particle [math](\rho)[/math] travel in opposite directions with respect to eachother ( ie; they are "back - to -back")
- This means that there is no preferential direction for the decay (the particles are distributed isotropically such that they are back-to-back)
Decay of Moving Particle to 2 Bodies (decay in flight)
- [math]P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}[/math]
Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles which perpendicular to the Z-axis (transverse components:[math]\vec{p}_{1,\perp}[/math] and [math]\vec{p}_{2,\perp}[/math]) are equal and opposite by conservation of momentum.
- [math]\vec{p}_{\perp}\equiv -\vec{p}_{2,\perp}[/math]
