Comparison of GEANT Simulation to Whitney Data

[math]\textbf{Navigation}[/math]

[math]\vartriangleleft [/math] [math]\triangle [/math] [math]\vartriangleright [/math]

Rates

Simulation	GEANT4(1cm target)	GEANT4(1cm target)	GEANT4(5cm target)	GEANT4(5cm target)	Whitney
Length of Target (cm)	1	1	5	5	5
[math]N_{incident}[/math]	4E7	4E8	6E6	6E7	6E7
[math]N_{events}[/math]	1026940	10270829	771161	4826141	1001700
[math]N_{events}(5^{\circ}-40^{\circ})[/math]
[math]N_{Moller}[/math]	975593	9757288	732603	4584834	951138
[math]N_{Moller(5^{\circ}-40^{\circ})}[/math]			217803	1362098
[math]t_{simulated}[/math] (s)	1.3E-5	1.3E-4	9.57E-6	9.62E-5	9.54E-5
Event Cross-Section (b)	0.61	0.61	0.61	0.38	0.079
Total Moller Cross-Section (b)	0.58	0.58	0.58	0.361	0.075
Individual Moller Cross-Section (b)	5.95E-7	5.94E-8	7.92E-7	7.87E-8	7.88E-8
Moller event rate per barn ([math]b^{-1}[/math])	1.68E6	1.68E6	1.26E6	1.27E7	1.27E7

Total dectector events occur for about 2.5% of the incident electrons on a LH2 target. We can assume that the Moller rate is 95% of the total event rate. We can assume the number of Moller events that occur within the DC range to be around 30% of the total Moller events occuring for the number of incident electrons for LH2 as well. Since the differential cross-section over the angel theta is proportional to the differtial cross-section over wire number we can dividing the Moller differential cross-section by the product of the density and length of the target material

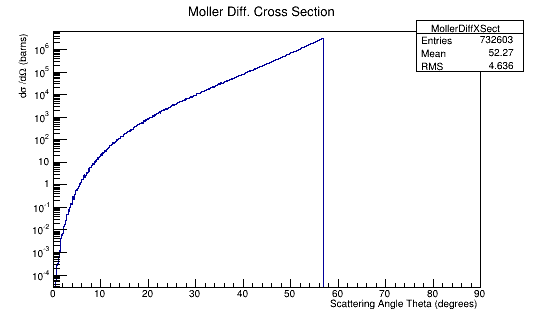
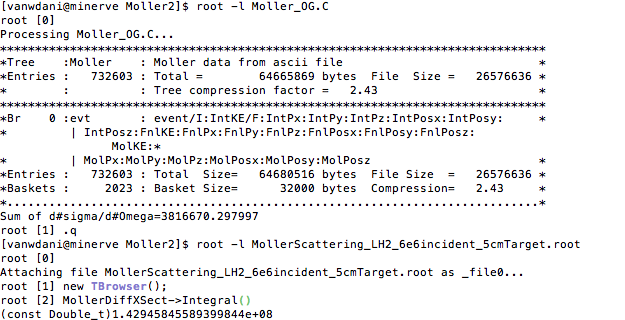
If we were to integrate the Moller Differential Cross Section