Difference between revisions of "Theoretical analysis of 2n accidentals rates"
| (402 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Production Analysis | go_back]] | [[Production Analysis | go_back]] | ||
| − | |||
| − | |||
| − | = | + | =Introduction= |
| − | + | A given photon pulse may cause multiple neutron-producing reactions, ranging from zero to "infinity" reactions. The number of neutron-producing reactions ''actually'' occurring in a given pulse is denoted by the random variable <math>n</math>, and is assumed to follow the Poissonian distribution. Each neutron-producing interaction is said to produce <math>v_{i}</math> correlated neutrons, where the random variable <math>v_{i}</math> is the distribution of the number of neutrons produced in a single neutron-producing reaction. Each of the <math>v_i\text{'}s</math> are independent and identically distributed random variables, and the purpose of the subscript is to distinguish between several distinct neutron-producing interactions that occur in a single pulse. | |
| − | |||
| − | |||
| − | |||
| − | + | The beam has a Bremsstrahlung end point of 10.5 MeV, which energetically allows for only two possible neutron-producing interactions, 1n-knochout and photofission. Thus, <math>v_{i}</math> is equal to the photofission neutron multiplicity, plus a contribution at <math>v_{i}=\text{1}</math> from 1n-knockout events. The analysis that follows does not need to distinguish between 1n-knockout events and photofission events that emit a single neutron, since in both cases, a single neutron is emitted that is uncorrelated with all other neutrons. | |
| − | , | + | The rate of detected accidentals can be estimated from the two-neutron "coincidence" rate of different pulse (DP) events, or in other words, the DP two-neutron rate. This is the rate of two-neutron events when examining pairs of two pulses – and there must be at least one event in each pulse for it to count as a two-neutron event. Under suitable conditions, the rate of accidentals is very close to 1/2 of DP two-neutron rate. |
| − | + | During the derivation of this result, a pulse is considered in which there are <math>n</math> neutron-producing interactions, where each individual reaction produces <math>v_i</math> correlated neutrons, where <math>i</math> ranges from 1 to <math>n</math>. This event is denoted as, <math>v_1...v_n</math>, and its probability by the expression, <math>p(v_1...v_n)</math>. | |
| − | |||
| − | + | ==Summary of what follows== | |
| − | : | + | [[File:SPDPVisualAid.png|thumb|350px|right| An example to illustrate the combinatorics of counting the number of accidentals available for detection. This example considers a hypothetical pulse in which there are three neutron-producing reactions, creating sets of two, three, and one correlated neutrons. The reactions can be paired together in three different ways. For each pair of reactions, the total number of accidentals is the product of the number of neutrons from each reaction.]] |
| − | The | ||
| − | + | To find the rate of detecting pairs of uncorrelated neutrons, first find the mean number of uncorrelated two-neutron pairs (i.e. accidentals) available for detection in a pulse, and then multiply this by the detector array's two-neutron efficiency. | |
| − | + | For single pulses, to calculate the average number of pairs available for detection, first calculate the average the number of ways to select pairs of two reactions from a pulse, given that each pulse has an average of <math>\lambda</math> reactions. Next, multiply this value by the average number of uncorrelated two-neutron pairs that can be formed among the neutrons produced from two independent reactions. The average number of neutron pairs formed between any two independent reactions is just <math>\bar{v}^2</math>, and the number of ways to choose two reactions from a set of <math>n</math> reactions is <math>\frac{1}{2}n(n-1)</math>. The average number of correlated neutron pairs available for detection in single pulses is given by the product: | |
| + | ::<math>\bar{v}^2E[\frac{1}{2}n(n-1)]</math> | ||
| − | + | where <math>E</math> is the expectation value. | |
| + | As we will see in the next section, since <math>n</math> follows the Poissonian distribution, this can be simplified to | ||
| − | ::<math> | + | ::<math>\frac{1}{2}\bar{v}^2\lambda^2</math> |
| − | + | For the case of two-neutron events in DP pairs, the same line of reasoning leads the following result: | |
| − | + | ||
| − | :: | + | ::<math>\bar{v}^2\lambda^2</math> |
| − | ::<math> | + | |
| + | ==Reference of variables== | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !variable !!Description | ||
| + | |- | ||
| + | |<math>n , n_1 , n_2</math> | ||
| + | |A random variable for the number of neutron producing reactions occurring in a single pulse. <math>n_1</math> and <math>n_2</math> are used to distinguish between the two different <math>n\text{'s}</math> of a two pulse pair. | ||
| + | |- | ||
| + | |<math>v</math>, <math>v_i</math> | ||
| + | |A random variable for the number of correlated neutrons produced by a single neutron-producing reaction in a given pulse. The index only distinguishes between distinct and independent instances of <math>v</math>. | ||
| + | |- | ||
| + | |<math>p(d^2)</math> || is the probability of detecting a pair of two uncorrelated neutrons, provided that we know nothing else about them except that they are uncorrelated.. | ||
| + | |- | ||
| + | |<math>\lambda</math>||Poissonian mean for the number of neutron-producing interactions per pulse. | ||
| + | |- | ||
| + | |<math>m_{sp}</math> || Represents the series <math>\sum_{i\neq j}v_iv_j</math>, which is the number of possible accidentals that exist in a given pulse. | ||
| + | |- | ||
| + | |<math>m_{dp}</math> ||Represents the series <math>(\sum_{i}^{n_1}v_i)\times(\sum_{j}^{n_2}v_j)</math>, which is the total number of two neutron pairs that can be formed across two separate pulses. | ||
| + | |- | ||
| + | |<math>t_{sp}</math> || The number of terms of the form <math>v_iv_j</math> in <math> m_{sp}</math>. | ||
| + | |- | ||
| + | |<math>t_{dp}</math> || The number of terms of the form <math>v_iv_j</math> in <math> m_{dp}</math>. | ||
| + | |- | ||
| + | |<math>SP_{acc}</math> || represents the event that an accidental is detected in a single pulse. | ||
| + | |- | ||
| + | |<math> DP_{acc}</math> || represents the event that a two-neutron pair is detected when examining events across two separate pulses. | ||
| + | |- | ||
| + | | <math>E[X]</math> || Denotes the expectation value of some quantity X over a large number of pulses. | ||
| + | |} | ||
| + | |||
| + | =Accidental estimation= | ||
| + | |||
| + | |||
| + | ==Assumptions and approximations== | ||
| + | There are two approximations which are required to make this result valid. | ||
| + | |||
| + | ===1. Poissonian statistics === | ||
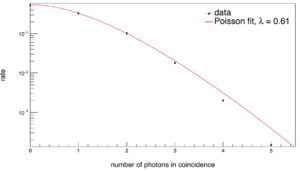
| + | [[File:2NcorrPhotonPoissonCoincFit.png| thumb|right|Distribution of the number of photons measured in coincidence with a Poisson fit. ]] | ||
| + | |||
| + | The number of neutron-producing reactions occurring per pulse, <math>n</math>, is assumed to follow the Poissonian distribution. | ||
| + | It can be seen from data, at least, that the number of photons per pulse follows the Poisson distribution (right). If ''m'' photons impinge on the target during a given pulse, each photon will have an independent probability, ''p'', of inducing a reaction. As a result, the distribution of the number of photo-induced reactions conforms to a binomial distribution with parameters ''m'' and ''p'', where ''m'' itself follows the Poisson distribution. A binomial distribution with the number of trials distributed according to the Poisson distribution, is also a Poisson distribution. Thus, the number of neutron producing reactions can safety assume to follow the Poisson distribution. | ||
| + | |||
| + | |||
| + | . | ||
| + | |||
| + | ===2. Small detection probability === | ||
| + | |||
| + | The probability of detecting two specific uncorrelated neutrons in a given pulse, denoted by <math>p(d^2)</math>, is independent of how many other neutrons are emitted in that same pulse. These two neutrons could be among, say, 8 other neutrons which are emitted in the same pulse, and the assumption is that <math>p(d^2)</math> has the same value as it would if no other neutrons are emitted. | ||
| + | |||
| + | This is only an approximation, however, since each detector can register at most one hit per pulse, and so the effective efficiency of the entire array drops as the number of particles emitted increases. In other words, it is being assumed that neutrons do not "compete" against one another for a chance to be detected. This approximation is justified because each detector covers only 0.5% out of <math>4\pi</math> sr, and the rate of detected two-neutron coincidences per pulse is on the order of 10E-5, and no triple neutron events were recorded. | ||
| + | I am making a point to address this, because it accounts for the fact that the SP/DP accidental ratio is significantly greater than 1/2 for photons, which are strictly accidentals. | ||
| + | |||
| + | This assumption can be expressed mathematically as: | ||
| + | |||
| + | ::<math>p(d^2|v_1...v_n) = p(d^2)</math> | ||
| + | |||
| + | As a result, to find the probability of detecting an accidental in a given pulse, simply count all possible accidental pairs in that pulse and multiply the result by <math>p(d^2)</math>: | ||
| + | |||
| + | ::<math>p(SP_{acc}) = m_{sp}*p(d^2)</math> | ||
| + | :where, | ||
| + | :<math>SP_{acc}</math> is the event that an accidental is detected. | ||
| + | :<math>m_{sp}</math> is the number of accidentals in a given pulse, or in other words, the number of ways to form pairs of two uncorrelated neutrons from the set of all neutrons produced in a given pulse. | ||
| + | |||
| + | When examining events in pulse pairs, if a neutron event occurs in the same detector in both pulses, the event with the larger time of flight is thrown out. This way, <math>p(d^2)</math> is the same for any pair of uncorrelated neutrons, whether they were produced during the same, or two separate pulses. Thus, the same line of reasoning used to find the approximate probability of detecting two uncorrelated neutrons in a single pulse, can be applied to the case of pulse pairs: | ||
| + | |||
| + | ::<math>p(DP_{acc}) = m_{dp}*p(d^2)</math> | ||
:where, | :where, | ||
| − | :<math> | + | :<math>DP_{acc}</math> is the event that a neutron is detected in both pulses |
| − | :<math> | + | :<math>m_{dp}</math> is the total number of two-neutron pairs that can be made across two pulses by selecting a neutron produced in each pulse. |
| + | |||
| + | ==Combinatorics== | ||
| + | ===Same pulses=== | ||
| + | The total number of accidentals in a given pulse, <math>m_{sp}</math> is equal to | ||
| + | |||
| + | ::<math>m_{sp} = \sum_{i\neq j}v_iv_j</math> | ||
| + | |||
| + | For example, consider a pulse with three fission events, producing sets of 2, 3, and 1 correlated neutrons. Counting the number of uncorrelated neutron pairs can be done as follows: | ||
| + | :<math>m_{sp} = v_1 v_2+v_1v_3+v_2v_3 = 2\times 3 + 2\times 1 + 3\times 1 = 11 \text{ pairs}</math> | ||
| + | |||
| + | As another example, consider 4 fissions producing 2, 5, 3, and 1 correlated neutrons, then we have: | ||
| + | :<math> m_{sp} = 2\times5 + 2 \times 3 + 2 \times 1 + 5\times3 + 5\times1 + 3\times1 = 41 \text{ pairs}</math> | ||
| + | |||
| + | Fortunately, there is no need to consider the value of <math>m_{sp}</math> for every possible set of <math>v_{i}\text{'s}</math>, since the final result will depend only on the average number of terms in the series <math>m_{sp}</math>, and on the expected value of <math>v</math>. The number of terms, denoted by <math>t_{sp}</math>, is equal to the number of ways to pick two reactions from a set of <math>n</math> distinct reactions. | ||
| + | |||
| + | ::<math>t_{sp} = \frac{1}{2}n(n-1)</math> | ||
| + | :where again, <math>n</math> is the number of neutron-producing reactions in a given pulse. | ||
| + | |||
| + | The expectation of <math>m_{sp}</math> over a large number of pulses, is expressible in terms of <math>E[t_{sp}]</math> and <math>E[v]</math>, where E denotes the expected value. This is possible because <math>m_{sp}</math> is a sum of products of independent random variables, and by the linearity of expectation, its expected value is equal to the sum of the product of the individual expectation values: | ||
| + | |||
| + | \begin{array}{lcl} | ||
| + | E[m_{sp}|n] &=& E[\sum_{i\neq j}v_iv_j|n]\\ | ||
| + | & = & \overbrace{\bar{v}^2 + \bar{v}^2 + ... +\bar{v}^2}^{t_{sp} \text{ terms}}\\ | ||
| + | &=&\frac{1}{2}n(n-1)\bar{v}^2 | ||
| + | \end{array} | ||
| + | |||
| + | The expression, <math>E[m_{sp}|n]</math>, is known as a conditional expectation, which means that the expectation is computed for some fixed <math>n</math>. The steps above use the fact that <math>m_{sp}</math> is a sum of terms of the form <math>v_iv_j</math>, and in taking the expectation of the sum, each term reduces identically to <math>\bar{v}^2</math>. | ||
| + | |||
| + | The total expectation of <math>m_{sp}</math> is computed by taking the expectation again, this time with respect to n | ||
| + | |||
| + | \begin{array}{lcl} | ||
| + | E[m_{sp}] & = & E \left [\frac{1}{2}n(n-1)\bar{v}^2 \right ]\\ | ||
| + | & = & \frac{1}{2} \left (E[n^2]- E[n]\right ) \bar{v}^2 | ||
| + | \end{array} | ||
| + | |||
| + | <math>n</math> is assumed to follow the Poissonian distribution, so its variance is equal to its mean, or stated mathematically, <math>E[n] = E[n^2] - E[n]^2</math>. Substituting <math>E[n]</math> with the variance in the expression for <math>E[m_{sp}]</math>, gives | ||
| + | |||
| + | \begin{array}{lcl} | ||
| + | E[m_{sp}] &=& \frac{1}{2}E[n]^2\bar{v}^2 \\ | ||
| + | & = & \frac{1}{2} \lambda^2\bar{v}^2 | ||
| + | \end{array} | ||
| + | where <math> \lambda</math> is the mean number of neutron producing reactions occurring per pulse. As argued in the assumptions and approximations section, the probability of detecting an accidental in some pulse, denoted by <math>P_{acc}</math>, is proportional to the number of accidentals available, times the two-neutron detection efficiency. To arrive at the final result, we take the expectation of <math>P_{acc}</math>: | ||
| + | |||
| + | \begin{array}{lcl} | ||
| + | E[P_{acc}] &=& E[m_{sp} \times p(d^2)] | ||
| + | \end{array} | ||
| + | |||
| + | By approximation (2.) discussed above, the two-neutron detection efficiency, <math>p(d^2)</math>, is independent of <math>m_{sp}</math>, and is therefore a constant, allowing it to be taken out of the expectation value: | ||
| + | \begin{array}{lcl} | ||
| + | E[P_{acc}] &=& E[m_{sp}]p(d^2) \\ | ||
| + | & = & \frac{1}{2} \lambda^2 \bar{v}^2 p(d^2) | ||
| + | \end{array} | ||
| + | |||
| + | <math>E[P_{acc}]</math> is itself a probability, but it may also be interpreted as the per-pulse accidental rate. | ||
| + | |||
| + | As we shall see, <math>p(d^2)</math> will also appear as a multiplicative constant in the result for DP events, allowing it to cancel in the ratio, SP/DP. | ||
| + | |||
| + | ===Different pulses=== | ||
| + | When forming pairs of uncorrelated neutrons across separate pulses, the total number of pairs is given by: | ||
| + | |||
| + | ::<math>m_{dp} = (\sum_{i=1}^{n_1}v_i)(\sum_{j=1}^{n_2}v_j)</math> | ||
| + | |||
| + | Here, <math> t_{dp}</math>, or the total number of terms of the form <math>v_iv_j</math> after expanding <math>m_{dp}</math>, is simply the product of the number of reactions in each pulse: | ||
| + | |||
| + | ::<math> t_{dp} = n_1 * n_2 </math> | ||
| + | |||
| + | The expected number of two-neutron pairs available in two-pulse events is: | ||
| + | |||
| + | ::<math> E[m_{dp}] = E[t_{dp}] *\bar{v}^2 </math> | ||
| + | |||
| + | Since the values of <math>n</math> from two separate pulse are independent, the linearity of expectation be applied to give, <math>E[t_{dp}] = \lambda^2</math>. Finally, the expected number of two-neutron pairs available when looking at DP events is: | ||
| − | + | ::<math> E[m_{dp}] = \lambda^2 \bar{v}^2</math> | |
| − | : | + | Following the same reasoning as for same pulse accidentals, the probability of a two-neutron event in a two pulse pair is: |
| − | + | \begin{array}{lcl} | |
| + | E[DP_{acc}] &=& E[m_{dp} \times p(d^2)] \\ | ||
| + | &=& \lambda^2 \bar{v}^2 \times p(d^2) | ||
| + | \end{array} | ||
Latest revision as of 20:57, 25 January 2018
Introduction
A given photon pulse may cause multiple neutron-producing reactions, ranging from zero to "infinity" reactions. The number of neutron-producing reactions actually occurring in a given pulse is denoted by the random variable , and is assumed to follow the Poissonian distribution. Each neutron-producing interaction is said to produce correlated neutrons, where the random variable is the distribution of the number of neutrons produced in a single neutron-producing reaction. Each of the are independent and identically distributed random variables, and the purpose of the subscript is to distinguish between several distinct neutron-producing interactions that occur in a single pulse.
The beam has a Bremsstrahlung end point of 10.5 MeV, which energetically allows for only two possible neutron-producing interactions, 1n-knochout and photofission. Thus, is equal to the photofission neutron multiplicity, plus a contribution at from 1n-knockout events. The analysis that follows does not need to distinguish between 1n-knockout events and photofission events that emit a single neutron, since in both cases, a single neutron is emitted that is uncorrelated with all other neutrons.
The rate of detected accidentals can be estimated from the two-neutron "coincidence" rate of different pulse (DP) events, or in other words, the DP two-neutron rate. This is the rate of two-neutron events when examining pairs of two pulses – and there must be at least one event in each pulse for it to count as a two-neutron event. Under suitable conditions, the rate of accidentals is very close to 1/2 of DP two-neutron rate.
During the derivation of this result, a pulse is considered in which there are neutron-producing interactions, where each individual reaction produces correlated neutrons, where ranges from 1 to . This event is denoted as, , and its probability by the expression, .
Summary of what follows
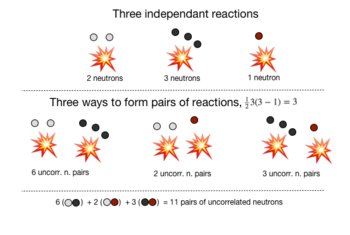
To find the rate of detecting pairs of uncorrelated neutrons, first find the mean number of uncorrelated two-neutron pairs (i.e. accidentals) available for detection in a pulse, and then multiply this by the detector array's two-neutron efficiency.
For single pulses, to calculate the average number of pairs available for detection, first calculate the average the number of ways to select pairs of two reactions from a pulse, given that each pulse has an average of reactions. Next, multiply this value by the average number of uncorrelated two-neutron pairs that can be formed among the neutrons produced from two independent reactions. The average number of neutron pairs formed between any two independent reactions is just , and the number of ways to choose two reactions from a set of reactions is . The average number of correlated neutron pairs available for detection in single pulses is given by the product:
where is the expectation value. As we will see in the next section, since follows the Poissonian distribution, this can be simplified to
For the case of two-neutron events in DP pairs, the same line of reasoning leads the following result:
Reference of variables
| variable | Description |
|---|---|
| A random variable for the number of neutron producing reactions occurring in a single pulse. and are used to distinguish between the two different of a two pulse pair. | |
| , | A random variable for the number of correlated neutrons produced by a single neutron-producing reaction in a given pulse. The index only distinguishes between distinct and independent instances of . |
| is the probability of detecting a pair of two uncorrelated neutrons, provided that we know nothing else about them except that they are uncorrelated.. | |
| Poissonian mean for the number of neutron-producing interactions per pulse. | |
| Represents the series , which is the number of possible accidentals that exist in a given pulse. | |
| Represents the series , which is the total number of two neutron pairs that can be formed across two separate pulses. | |
| The number of terms of the form in . | |
| The number of terms of the form in . | |
| represents the event that an accidental is detected in a single pulse. | |
| represents the event that a two-neutron pair is detected when examining events across two separate pulses. | |
| Denotes the expectation value of some quantity X over a large number of pulses. |
Accidental estimation
Assumptions and approximations
There are two approximations which are required to make this result valid.
1. Poissonian statistics
The number of neutron-producing reactions occurring per pulse, , is assumed to follow the Poissonian distribution. It can be seen from data, at least, that the number of photons per pulse follows the Poisson distribution (right). If m photons impinge on the target during a given pulse, each photon will have an independent probability, p, of inducing a reaction. As a result, the distribution of the number of photo-induced reactions conforms to a binomial distribution with parameters m and p, where m itself follows the Poisson distribution. A binomial distribution with the number of trials distributed according to the Poisson distribution, is also a Poisson distribution. Thus, the number of neutron producing reactions can safety assume to follow the Poisson distribution.
.
2. Small detection probability
The probability of detecting two specific uncorrelated neutrons in a given pulse, denoted by , is independent of how many other neutrons are emitted in that same pulse. These two neutrons could be among, say, 8 other neutrons which are emitted in the same pulse, and the assumption is that has the same value as it would if no other neutrons are emitted.
This is only an approximation, however, since each detector can register at most one hit per pulse, and so the effective efficiency of the entire array drops as the number of particles emitted increases. In other words, it is being assumed that neutrons do not "compete" against one another for a chance to be detected. This approximation is justified because each detector covers only 0.5% out of sr, and the rate of detected two-neutron coincidences per pulse is on the order of 10E-5, and no triple neutron events were recorded. I am making a point to address this, because it accounts for the fact that the SP/DP accidental ratio is significantly greater than 1/2 for photons, which are strictly accidentals.
This assumption can be expressed mathematically as:
As a result, to find the probability of detecting an accidental in a given pulse, simply count all possible accidental pairs in that pulse and multiply the result by :
- where,
- is the event that an accidental is detected.
- is the number of accidentals in a given pulse, or in other words, the number of ways to form pairs of two uncorrelated neutrons from the set of all neutrons produced in a given pulse.
When examining events in pulse pairs, if a neutron event occurs in the same detector in both pulses, the event with the larger time of flight is thrown out. This way, is the same for any pair of uncorrelated neutrons, whether they were produced during the same, or two separate pulses. Thus, the same line of reasoning used to find the approximate probability of detecting two uncorrelated neutrons in a single pulse, can be applied to the case of pulse pairs:
- where,
- is the event that a neutron is detected in both pulses
- is the total number of two-neutron pairs that can be made across two pulses by selecting a neutron produced in each pulse.
Combinatorics
Same pulses
The total number of accidentals in a given pulse, is equal to
For example, consider a pulse with three fission events, producing sets of 2, 3, and 1 correlated neutrons. Counting the number of uncorrelated neutron pairs can be done as follows:
As another example, consider 4 fissions producing 2, 5, 3, and 1 correlated neutrons, then we have:
Fortunately, there is no need to consider the value of for every possible set of , since the final result will depend only on the average number of terms in the series , and on the expected value of . The number of terms, denoted by , is equal to the number of ways to pick two reactions from a set of distinct reactions.
- where again, is the number of neutron-producing reactions in a given pulse.
The expectation of over a large number of pulses, is expressible in terms of and , where E denotes the expected value. This is possible because is a sum of products of independent random variables, and by the linearity of expectation, its expected value is equal to the sum of the product of the individual expectation values:
\begin{array}{lcl} E[m_{sp}|n] &=& E[\sum_{i\neq j}v_iv_j|n]\\ & = & \overbrace{\bar{v}^2 + \bar{v}^2 + ... +\bar{v}^2}^{t_{sp} \text{ terms}}\\ &=&\frac{1}{2}n(n-1)\bar{v}^2 \end{array}
The expression, , is known as a conditional expectation, which means that the expectation is computed for some fixed . The steps above use the fact that is a sum of terms of the form , and in taking the expectation of the sum, each term reduces identically to .
The total expectation of is computed by taking the expectation again, this time with respect to n
\begin{array}{lcl} E[m_{sp}] & = & E \left [\frac{1}{2}n(n-1)\bar{v}^2 \right ]\\ & = & \frac{1}{2} \left (E[n^2]- E[n]\right ) \bar{v}^2 \end{array}
is assumed to follow the Poissonian distribution, so its variance is equal to its mean, or stated mathematically, . Substituting with the variance in the expression for , gives
\begin{array}{lcl} E[m_{sp}] &=& \frac{1}{2}E[n]^2\bar{v}^2 \\ & = & \frac{1}{2} \lambda^2\bar{v}^2 \end{array} where is the mean number of neutron producing reactions occurring per pulse. As argued in the assumptions and approximations section, the probability of detecting an accidental in some pulse, denoted by , is proportional to the number of accidentals available, times the two-neutron detection efficiency. To arrive at the final result, we take the expectation of :
\begin{array}{lcl} E[P_{acc}] &=& E[m_{sp} \times p(d^2)] \end{array}
By approximation (2.) discussed above, the two-neutron detection efficiency, , is independent of , and is therefore a constant, allowing it to be taken out of the expectation value: \begin{array}{lcl} E[P_{acc}] &=& E[m_{sp}]p(d^2) \\ & = & \frac{1}{2} \lambda^2 \bar{v}^2 p(d^2) \end{array}
is itself a probability, but it may also be interpreted as the per-pulse accidental rate.
As we shall see, will also appear as a multiplicative constant in the result for DP events, allowing it to cancel in the ratio, SP/DP.
Different pulses
When forming pairs of uncorrelated neutrons across separate pulses, the total number of pairs is given by:
Here, , or the total number of terms of the form after expanding , is simply the product of the number of reactions in each pulse:
The expected number of two-neutron pairs available in two-pulse events is:
Since the values of from two separate pulse are independent, the linearity of expectation be applied to give, . Finally, the expected number of two-neutron pairs available when looking at DP events is:
Following the same reasoning as for same pulse accidentals, the probability of a two-neutron event in a two pulse pair is:
\begin{array}{lcl} E[DP_{acc}] &=& E[m_{dp} \times p(d^2)] \\ &=& \lambda^2 \bar{v}^2 \times p(d^2) \end{array}