2NCorr Photon flux estimate

Overview

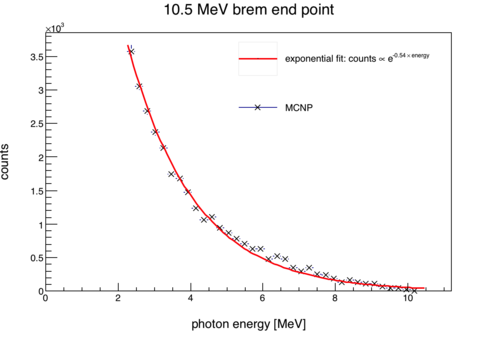
An estimated lower bound for the photon flux throughout the experiment can be calculated from the data of a D2O target. The measured neutron rate from D2O depends on the following: the (G,n) cross-section as a function of energy, the energy distribution of the brem photons, target geometry, detector efficiency, and photon flux. The (G,n) cross-sections are known and the brem energy distribution can be taken from an MCNP simulation. The only remaining unknown variables are photon flux and detector efficiency. By setting detector efficiency to 100%, and considering only geometric effects (i.e. solid angle), a lower bound can be placed on the photon flux incident on all targets.

Plots

• 

  Energy distribution of collimated bremsstrahlung photons from the passage of 10.5 MeV electrons through 1" of Al. Data is taken from an MCNP simulation.

Calculation

The measured neutron rate is given by:

[math]\int_{2.3}^{10.5}\! N_{\gamma}P(E)*P(n_0|E)*\epsilon(E)\,dE[/math]

[math]N_{\gamma}[/math] is the number of photons incident on the target between 2.3 MeV (the threshold for photo-disintegration of D2O), and 10.5 MeV (the brem end-point energy)

[math]E[/math] is photon energy

[math]\epsilon(E)[/math] is the detector efficiency

[math]P(n_0|E) [/math] is the probability of a photo-disintegration event given that the photon has energy E.

[math]P(E) [/math] is the probability of a photon having energy E.