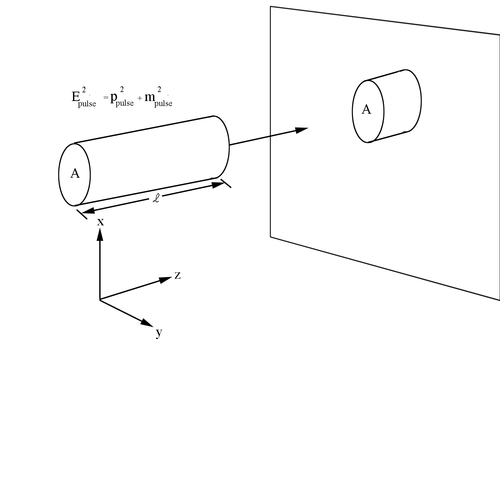
Flux of Incoming Particles

Flux of Incoming Particles

[math]I=\frac{dq}{dt}[/math]

[math]dq=nAlq \qquad dt=\frac{l}{v_d}[/math]

[math]E^2 \equiv p^2+m^2[/math]

[math]E^2=\S Using the operator relations \lt center\gt \lt math\gt E=i\hbar \frac{\partial}{\partial t} \qquad \vec p=i\hbar \nabla[/math]

We can obtain the relativitic Schrödinger equation, also known as the Klein-Gordon equation.

[math]-\frac{\partial^2 \phi}{\partial t^2}+\nabla^2 \phi=m^2 \phi[/math]

[math]\frac{\partial}{\partial t}\left [i \left (\phi^*\frac{\partial \phi}{\partial t}-\phi \frac{\partial \phi^*}{\partial t} \right ) \right ]+\vec \nabla \cdot \left [-i\left (\phi^*\vec \nabla \phi-\phi \vec \nabla \phi^* \right ) \right ]=0[/math]

[math]\phi=Ne^{i\vec p \cdot \vec x -iEt}[/math]

[math]\rho=i(-2iE)|N|^2=2E|N|^2[/math]

[math]\vec j=-i(2i\vec p)|N|^2=2\vec p|N|^2[/math]

The number of particles in a beam passing through a unit area per unit time is

[math]\frac{Number\ of\ beam\ particles}{time\times Volume}=[/math] [math]\frac{|\vec v_1|2E_1}{V}[/math]

The number of stationary target particles per unit volume is

[math]\frac{Number\ of\ target\ particles}{Volume}[/math]

[math]\frac{2E_2}{V}[/math]

Initial flux=[math]|\vec v_1|\frac{2E_1}{V} \frac{2E_2}{V}[/math]

[math]F=2E_1 2E_2|\vec {v}_1-\vec {v}_2|=4|E_1E_2\vec v_{21}|[/math]

where [math]v_{21}[/math] is the relative velocity between the particles in the frame where particle 1 is at rest

[math]\mathbf P_1 \cdot \mathbf P_2 = E_{1}E_{2}-(\vec p_1 \vec p_2)= E_{1}E_{2}[/math]

Using the relativistic definition of energy

[math]E^2 \equiv p^2+m^2=m^2[/math]

[math]\rightarrow \mathbf P_1 \cdot \mathbf P_2 =mE_{2}[/math]

Letting [math]E_{21}\equiv E_2[/math] be the energy of particle 2 wiith respect to particle 1, the relativistic energy equation can be rewritten such that

[math]|p_{21}^2| =E_{21}^2-m^2=\frac{(\mathbf P_1 \cdot \mathbf P_2)^2}{m^2}-m^2=\frac{(\mathbf P_1 \cdot \mathbf P_2)^2-m^4}{m^2}[/math]

where similarly [math]p_{21}[/math] is defined as the momentum of particle 2 with respect to particle 1.

The relative velocity can be expressed as

[math] v_{21}=\frac{|\vec p_{21}|}{E_{21}}[/math]

[math]F=2E_1 2E_2|\vec {v}_1-\vec {v}_2|=4|mE_{21}\vec v_{12}|=4|mE_{21}\frac{|\vec p_{21}|}{E_{21}}|=4m|\vec p_{21}|[/math]

The invariant form of F is

[math]F=4\sqrt{(\mathbf P_1 \cdot \mathbf P_2)^2-m^4}[/math]

[math]\mathbf P_1 \cdot \mathbf P_2 = E_{1}E_{2}-(\vec p_1 \vec p_2)[/math]

where in the center of mass frame [math]E_1=E_2[/math] and [math] \vec p_1^*=-\vec p_2^*[/math]

[math]\mathbf P_1 \cdot \mathbf P_2 = E_1^2+\vec p_1\,^{*2}[/math]

[math]F=4\sqrt{(E_1^2+\vec p_1\,^{*2})^2-m^4}=4\sqrt{(\vec p_1 \,^{*2}+m^2+\vec p_1\,^{*2})^2-m^4}[/math]

[math]F=4\sqrt{(2\vec p_1\,^{*2}+m^2)^2-m^4}=4\sqrt{4\vec p_1\,^{*4}+m^4+4\vec p_1\,^{*2}m-m^4}[/math]

[math]F_{cms}=4 \sqrt {4m^2\vec p_1\,^{*2}+4\vec p_1 \,^{*4}}[/math]

[math]F_{cms}=4 \sqrt {\vec p_1\,^{*2}4(m^2+\vec p_1 \,^{*2})}[/math]

As shown earlier

[math]s_{CM}=4(m^2+\vec p_1 \,^{*2})[/math]

[math]F_{cms}=4 \sqrt {\vec p_1^*\,^2s}[/math]