Difference between revisions of "Phi Dependent Components"
Jump to navigation
Jump to search
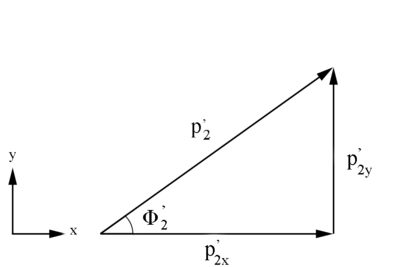
Figure 4: Definition of Moller electron variables in the Lab Frame in the x-y plane.
Similarly,
where
and using
this gives
which gives
Similarly, using
| Line 2: | Line 2: | ||
[[VanWasshenova_Thesis#Determining_wire-theta_correspondence|<math>\vartriangleleft </math>]] | [[VanWasshenova_Thesis#Determining_wire-theta_correspondence|<math>\vartriangleleft </math>]] | ||
| − | [[VanWasshenova_Thesis# | + | [[VanWasshenova_Thesis#Weighted_Isotropic_Distribution_in_Lab_Frame|<math>\triangle </math>]] |
[[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleright </math>]] | [[CED_Verification_of_DC_Angle_Theta_and_Wire_Correspondance|<math>\vartriangleright </math>]] | ||
Revision as of 14:33, 30 May 2017
Since only the z direction is considered to be the relativistic direction of motion, this implies that the x and y components are not effected by a Lorentz transformation and remain the same in the CM and Lab frame. Holding the angle Phi constant at an initial value of 10 degrees, allows us to find the x and y components.

Checking on the sign from the cosine results for
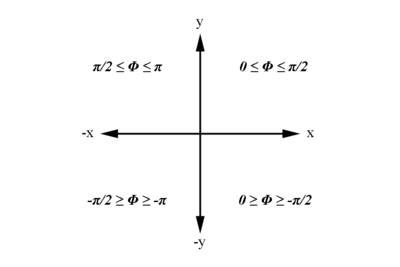
We have the limiting range that must fall within:

Examining the signs of the components which make up the angle in the 4 quadrants which make up the xy plane: