Difference between revisions of "Determining wire-theta correspondence"
| Line 32: | Line 32: | ||
| − | The first guard wire can be found at 4.694 degrees above the beam line. This position can be taken as the starting position for the wire normal plane. | + | The angle thmin is defined as the polar angle to the first guard wire’s (in the first guard wire plane) midpoint |
| + | where the wire mid-point is the intersection of the wire with the chamber mid-plane. The first guard wire can be found at 4.694 degrees above the beam line. This position can be taken as the starting position for the wire normal plane. | ||
Revision as of 20:14, 15 May 2017
Determing Wire-Theta Correspondence
To associate the hits with the Moller scattering angle theta, the occupancy plots of the drift chamber hits by means of wire numbers and layer must be translated using the physical constraints of the detector. Using the data released for the DC:
DC: Drift Chambers(specs)
DC Geometry(geom)
At 25 degrees above the beam line direction, we can create a line that is perpendicular to the plane of the wires, which are at 65 degrees above the reverse beam line direction. This line will be a perpendicular line with respect to all parallel layers of wires with respect to the initial guard wire plane. We can use this geometry and dist2target, which is the perpendicular length from the origin (0,0,0) to the plane of the first guard wire, to calculate other distances.
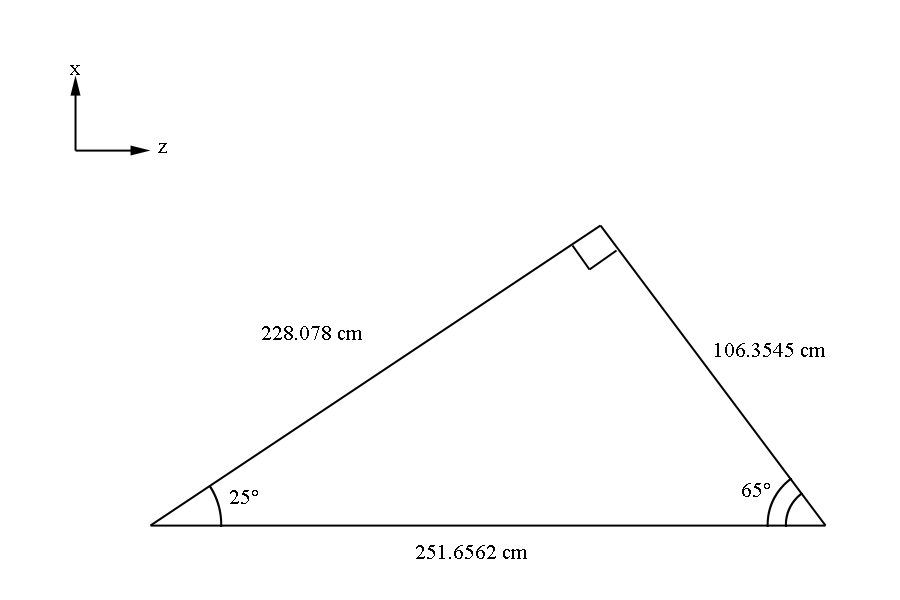
The parallel planes of wires are shown in the image below.
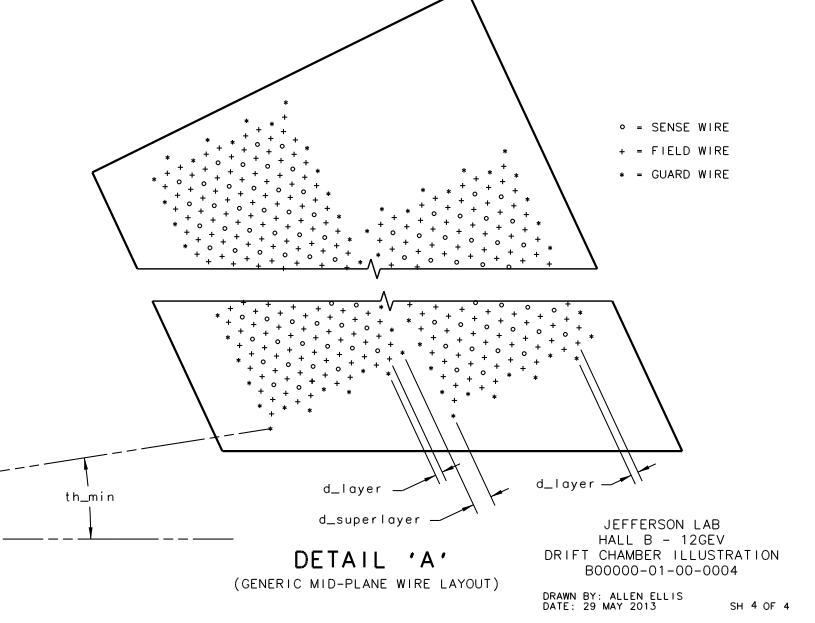
The angle thmin is defined as the polar angle to the first guard wire’s (in the first guard wire plane) midpoint
where the wire mid-point is the intersection of the wire with the chamber mid-plane. The first guard wire can be found at 4.694 degrees above the beam line. This position can be taken as the starting position for the wire normal plane.
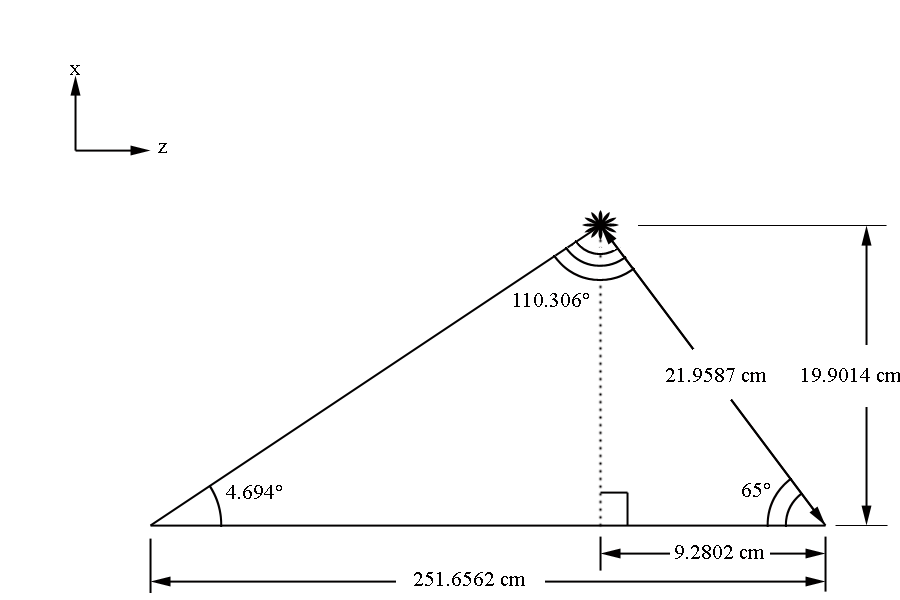
Using the law of sines
Making a right triangle,
Examining the geometry file, we can see that each plane, not just the plane of the sense wires, is separated by a distance of
We can use the geometry of the wire placements to find the separation distance between two adjacent sense wires on the same plane
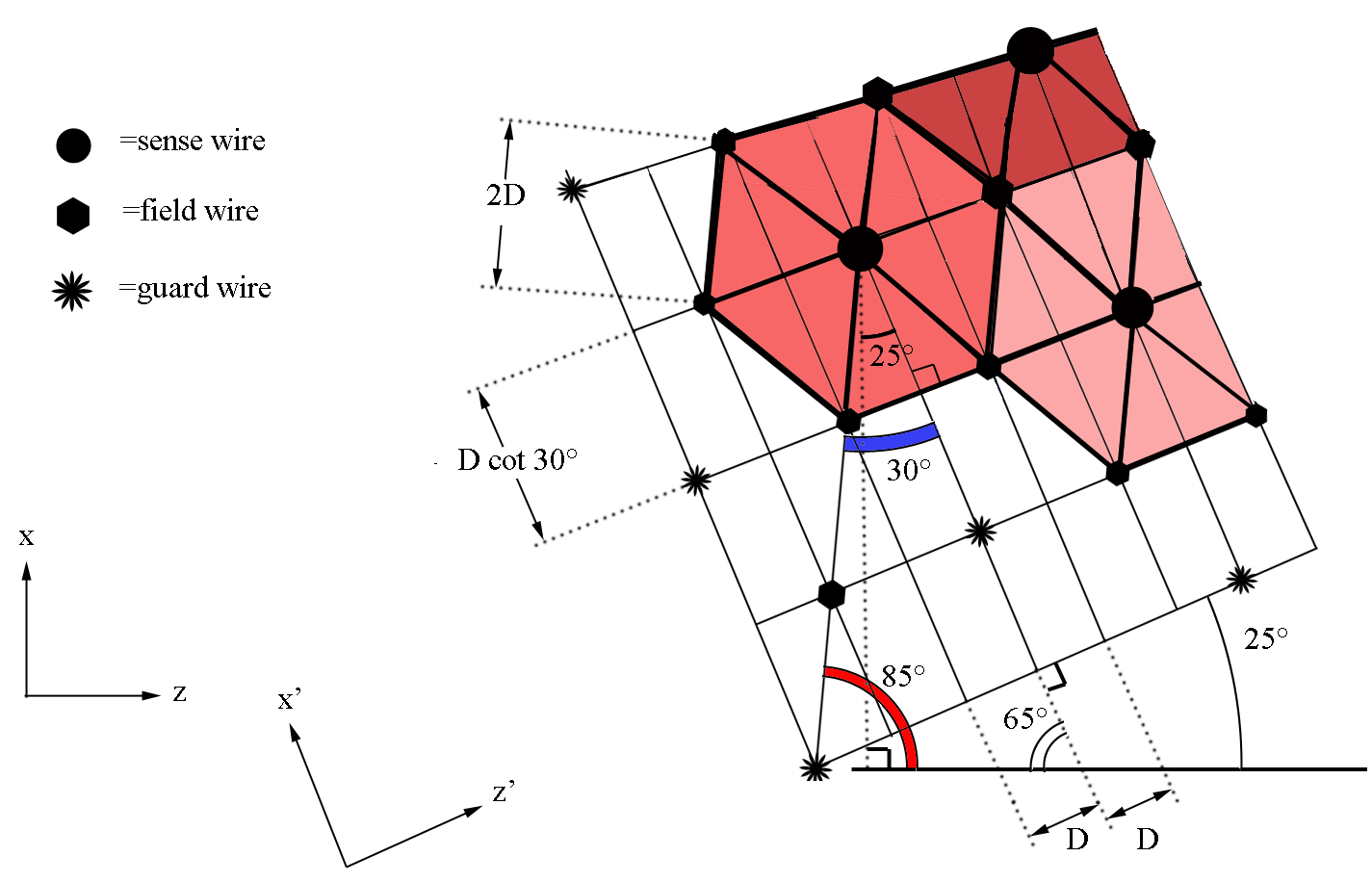
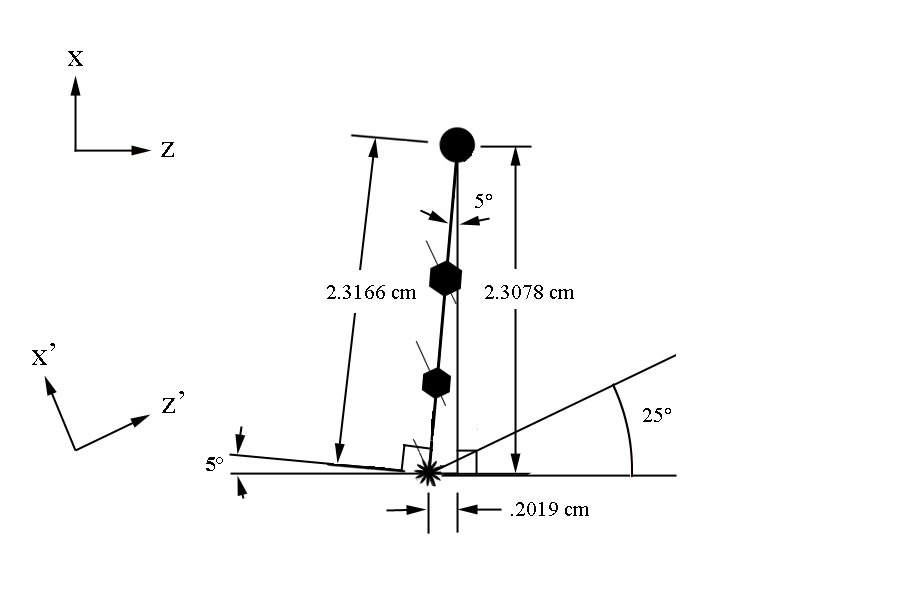
The starting position for sense wires with respect to the first guard wire at midplane, can be found to be at:
Since the separation between adjacent sense wires is uniform and at a set angle of 25 degrees with respect to the beam line, we can use this fact to determine the angle theta each wire makes when measured from the vertex.
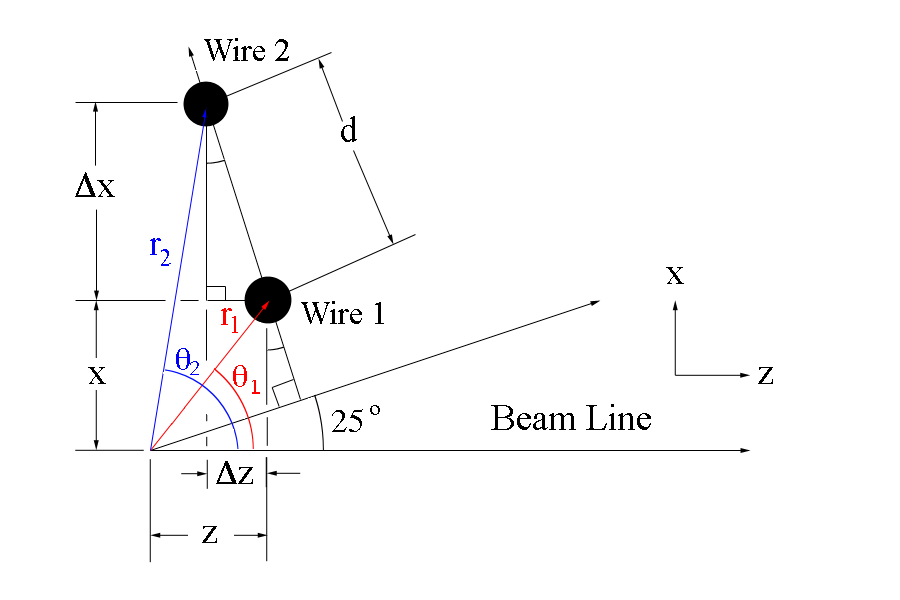
The new x and z coordinates for wire 2 can be found using the change in the components
This can be extended to any point along the same wire plane, starting from the coordinates for wire 1 minus the difference in position to the next wire crossing on the plane.
The angle theta that the wire makes with the vertex is given by
For the values found earlier for the starting position: