Difference between revisions of "PAA Selenium"

From New IAC Wiki
Jump to navigation Jump to search
Line 234: Line 234:
 
<math>\frac{{58 \atop 28\; }Ni (\gamma,n){57 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{12.1}^{24.2}\sigma dE}{Abundance \times \int_{12}^{24.2}\sigma dE} = \frac{0.68077 \times 214.047}{0.498 \times 1003.92} = 0.29 = \frac{\sigma_{Ni-57}}{\sigma_{Se-79}}</math>
 
<math>\frac{{58 \atop 28\; }Ni (\gamma,n){57 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{12.1}^{24.2}\sigma dE}{Abundance \times \int_{12}^{24.2}\sigma dE} = \frac{0.68077 \times 214.047}{0.498 \times 1003.92} = 0.29 = \frac{\sigma_{Ni-57}}{\sigma_{Se-79}}</math>
  
−
<math>\frac{N_{Se-79}}{N_{Ni-57}} = \left ( \frac{\sigma_{Se-79}}{\sigma_{Ni-57} }\right ) \left (  \frac{\lambda_{Ni-57}}{\lambda_{Se-79}}\right ) = \left ( \frac{1003.92}{214.047} \right ) \left (  \frac{0.0041 years}{327000} \right ) </math>
+
<math>\frac{N_{Se-79}}{N_{Ni-57}} = \left ( \frac{\sigma_{Se-79}}{\sigma_{Ni-57} }\right ) \left (  \frac{\lambda_{Ni-57}}{\lambda_{Se-79}}\right ) = \left ( \frac{1003.92}{214.047} \right ) \left (  \frac{0.0041}{327000} \right ) </math>
  
 
Segebade has a table of ratios of specific activities of certain elements compared to Ni-57. The section starts on page 167, but the ratios with selenium are found on page 176
 
Segebade has a table of ratios of specific activities of certain elements compared to Ni-57. The section starts on page 167, but the ratios with selenium are found on page 176

Revision as of 17:18, 1 November 2016

Using PAA ro measure Selenium concentrations.

According to Krouse<ref name="Krous1962"> H.R. Krause and H.G. Thode,"Thermodynamic Properties and Geochemistry of Iosotopic Compounds of Selenium",.Can. J. Chem., vol 40, pg 367</ref> , the fractional concentration of Se-82/Se-76 in plant material is observed to be less than from primordial (meteoric) concentrations by as much as 1.2%. Anaerobic bacteria are known to reduce selenates and senelites in biological systems. This may be the reason plant material has fractionation of selenium isotopes. They also observe excess concentrations of up to 0.4% in soil.


Plant material appears to detect environmental selenium.

Can one use plant material to measure the provenance of selenium?

Natural abundance of selenium

Isotope Abundance
Se-74 0.86%
Se-76 9.23%
Se-77 7.60%
Se-78 23.69%
Se-80 49.80%
Se-82 8.82%

Possible reactions

Reaction Half-life Relative activity Gamma-rays, keV (BR)
Se-74(gamma,n)Se-73 7.1 h 1.5E-1 361 (100)
Se-74(gamma,n)Se-73m 39 m 3.2 402 (4)
Se-74(gamma,np)As-72 26 h 1.0E-3 834 (100)
Se-76(gamma,n)Se-75 120 d 1.3E-2 265(29)
Se-77(gamma,p)As-76 26.4 h 4.4E-2 559(44)
Se-78(gamma,p)As-77 38.8 h 8.6E-2 239(2)
Se-80(gamma,n)Se-79m 3.9 m 5.9 96(10)
Se-80(gamma,np)As-78 1.5 h 2.2E-2 614(54)
Se-80(gamma,p)As-79 8.2 m 1.3 96(9)
Se-80(gamma,[math]a[/math]p)Ge-75 83 m 2.8E-1 265(11)

Can one perform PAA measurements of Se-82 and Se-76?

Neutron knockout of Se-82

If you knock a neutron out of Se-82 you produce the unstable isotope Se-81 which Beta emitts with half life of 18 min and a meta-state that emmits a 103 keV gamma with a 57 minute half life.

[math]{82 \atop 34\; }Se (\gamma,n){81 \atop \; }Se[/math]

Other prominent photons

260 & 276 keV for the 57 minute half life isotope

Neutron knockout of Se-76

If you knock a neutron out of Se-76 you produce the unstable isotope Se-75 which has a half life of 119 days.

[math]{76 \atop\; }Se (\gamma,n){75 \atop \; }Se[/math]

The prominent photons emitted have the following energies

136, 264, and 279 keV


The article below describes how plant material and soil contain Se-76 to Se-82 ratios that differ from other natural samples by 1.5%. They argue that it is due to the bacteria living in plant material.

File:Krouse CanJournChem 40 1962 p367.pdf

Plant material is a natural way to sample the selenium content to determine if there are difference isotopic ratios due to the impact of human activities on the environment.


Relative Yield Calculations

For this section, I am interested in finding the relative yield of Se-79 when compared to Se-81 and Se-75. Cross sections were found at this website: http://www-nds.indcentre.org.in/exfor/servlet/X4sSearch5?EntryID=220070

Cross-section

Below is a sample table of the cross section of a [math]{80 \atop 34\; }Se (\gamma,n){79 \atop \; }Se[/math] reaction. The beta endpoint for this long lived isotope is 150 keV with the highest intensity photon lines at 11 keV.

Energy (MeV) Cross Section( millibarns) ** Energy (MeV) Cross Section (millibarns) ** Energy (MeV) Cross Section (millibarns)
10.02 7.1 +/- 0.2 ** 15.02 110.9 +/- 4.6 ** 20.02 83 +/- 5.7
10.22 10.3 +/- 0.4 ** 15.22 118.9 +/- 4.1 ** 20.22 79.9 +/- 6.2
10.42 12.9 +/- 0.5 ** 15.42 125.8 +/- 5.5 ** 20.42 67.1 +/- 7.2
10.62 16.2 +/- 0.5 ** 15.62 132.9 +/- 4.5 ** 20.62 70.9 +/- 6.6
10.82 19.2 +/- 0.6 ** 15.82 132.7 +/- 5.9 ** 20.82 72.2 +/- 7.6
11.02 22 +/- 0.6 ** 16.02 127.6 +/- 5.6 ** 21.02 66.8 +/- 6.5
11.22 23.8 +/- 1 ** 16.22 132.4 +/- 5.3 ** 21.22 69.7 +/- 7
11.42 28 +/- 1 ** 16.42 130 +/- 7.6 ** 21.42 68.2 +/- 8.4
11.62 28.6 +/- 1.2 ** 16.62 125.4 +/- 6.2 ** 21.62 68.6 +/- 7.4
11.82 30.4 +/- 1.5 ** 16.82 137.4 +/- 6.7 ** 21.82 60.9 +/- 7.3
12.02 33 +/- 1.4 ** 17.02 138.1 +/- 7.5 ** 22.02 58.5 +/- 7.3
12.22 34.9 +/- 1.8 ** 17.22 130.4 +/- 8.3 ** 22.22 56 +/- 7.8
12.42 37.6 +/- 1.4 ** 17.42 114.9 +/- 6 ** 22.42 69.7 +/- 7.7
12.62 41.5 +/- 2 ** 17.62 110.8 +/- 6 ** 22.62 60.1 +/- 8.8
12.82 43.6 +/- 2.5 ** 17.82 104.4 +/- 7.4 ** 22.82 60.9 +/- 8.7
13.02 46.7 +/- 2.8 ** 18.02 108.7 +/- 6.6 ** 23.02 58.8 +/- 9.3
13.22 51.9 +/- 2.6 ** 18.22 102.4 +/- 7.3 ** 23.22 50.6 +/- 9.7
13.42 56.7 +/- 1.5 ** 18.42 104.3 +/- 5.7 ** 23.42 31.5 +/- 8.7
13.62 61.4 +/- 2.9 ** 18.62 104.1 +/- 5.5 ** 23.62 37.7 +/- 8.7
13.82 69.5 +/- 3.3 ** 18.82 91.1 +/- 7.8 ** 23.82 29.5 +/- 10.2
14.02 78.7 +/- 4.4 ** 19.02 90.5 +/- 5.5 ** 24.02 32.4 +/- 8.6
14.22 84.9 +/- 3.6 ** 19.22 85.7 +/- 6.2 ** 24.22 32.8 +/- 9.6
14.42 93.3 +/- 2.7 ** 19.42 91.4 +/- 6.6
14.62 100.5 +/- 4 ** 19.62 84.9 +/- 5.6
14.82 105.1 +/- 4.6 ** 19.82 90.3 +/- 8.1

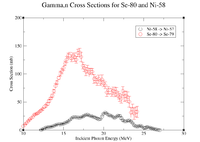
Similar data can be found in the link above. Below is the plot for all the reactions of interest.

Below is a plot of 3 different isotopes of selenium with their cross sections as a function of energy.

PhotonE vs XSect.png

Now to find the relative yields, I approximated the integral the above graph using a left hand Riemann sum with an interval width of 1 MeV and multiplied it by the natural abundance in the sample. Below is a table of the reactions and their integrated cross sections.


Reaction Abundance Integrated Cross Section (Mev * mb)
Se-82(gamma,n)Se-81 8.82% 1102.9
Se-80(gamma,n)Se-79 49.8% 1062.8
Se-76(gamma,n)Se-75 9.23% 836.5

Below are the equations for the relative yield of each isotope.


[math]\frac{{76 \atop 34\; }Se (\gamma,n){75 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{24.02}\sigma dE}{Abundance \times \int_{10.02}^{24.02}\sigma dE} = \frac{0.0923 \times 836.5}{0.498 \times 1062.8} = 0.15 = \frac{\sigma_{Se-75}}{\sigma_{Se-79}}[/math]


[math]\frac{{82 \atop 34\; }Se (\gamma,n){81 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{10.02}^{24.02}\sigma dE}{Abundance \times \int_{10.02}^{24.02}\sigma dE} = \frac{0.0882 \times 1102.9}{0.498 \times 1062.8} = 0.18[/math]

Activity Productions

Let

[math]N(t)[/math] = The number of activated atoms per cubic cm at time [math]t[/math]
[math]\mathcal{N}[/math] =The number density of the target = [math]\frac{\rho N_A}{A}[/math][ Atoms/cm^3]
[math]\rho[/math] = material density [g/cm^3]
[math]N_A[/math] = Avagadro's number = [math]6 \times 10^{23}[/math] g/mole
[math]A[/math] = Atomic Number
[math] \phi[/math] = incident photon flux ( photons/sec/cm/cm)


The rate of activated nuclei production is estimated by subtracting the rate of decay from the rate of production

[math]\frac{dN(t)}{dt} = N \sigma \phi - \lambda N(t)[/math]

where

[math]\lambda[/math] = half life of activated nucleus

[math]\Rightarrow N(t) = \frac{N \sigma \phi}{\lambda}\left ( 1 - e^{-\lambda t} \right )[/math]

The production rate ratio of Se-79 to Se-75 is

[math]\frac{N_{Se-79}}{N_{Se-75}} = \left ( \frac{\sigma_{Se-79}}{\sigma_{Se-75} }\right ) \left ( \frac{\lambda_{Se-75}}{\lambda_{Se-79}}\right ) = \left ( \frac{100}{15} \right ) \left ( \frac{119}{10^8} \right ) [/math]

Experiments

Nickel Normalization

Talk about Nickel reaction, give example of Nickel rates for 511 and 1377 keV lines. Run condition for examples below.

Ni-08-22-13

PAA_8-22-13#runlist


Using a 45 MeV linac (Jack) you get 75 uCi of Nickel per (gram Kw hr)

If using a 25 meV machine at 1 kW power, how ling should I run to keep 1 g of natural Selium from having a Se-79 Activiy less than 16 pCi?


Here is the data for the cross section of Ni-58([math]\gamma[/math],n)Ni-57 data

http://www-nds.indcentre.org.in/exfor/servlet/X4sGetSubent?reqx=119235&subID=220597006&plus=1

When comparing this data to the Se-80([math]\gamma[/math],n)Se-79 reaction, we must be careful when handling the bin sizes. The data for the Se-79 reaction is binned by intervals of 0.2 MeV, while the Ni-57 data is binned by intervals of 0.1 MeV. To create coarser bins, I must take the 3 data points from the Nickel data and get an average value, then plot that value centered at the midpoint of these two values. For example, I would take 10.1,10.2, and 10.3 MeV and average their values and plot at 10.2 MeV. Below is the plot:

XSect Ni58 Se80 xmgrace.png

Using a left handed Riemann Sum on each set of cross section data (The Selenium 79 reaction and the Nickel 58 reaction), the relative activity between the nickel isotopes and the selenium isotopes can be found. For the Nickel reaction I used a rectangular width equal to the bin size of the measurements, which was 0.1 MeV. Similarly for the selenium I had to use a bin size of 0.2 MeV while rounding the values down to the nearest tenth, i.e. 10.02 becomes 10.0, 10.22 becomes 10.2 and so on.

Reaction Integrated Cross Section (mb)
Se-80(gamma,n)Se-79 1003.92
Ni-58(gamma,n)Ni-57 214.047

[math]\frac{{58 \atop 28\; }Ni (\gamma,n){57 \atop \;Se}}{{80 \atop 34\; }Se (\gamma,n){79 \atop \;Se}} = \frac{Abundance \times \int_{12.1}^{24.2}\sigma dE}{Abundance \times \int_{12}^{24.2}\sigma dE} = \frac{0.68077 \times 214.047}{0.498 \times 1003.92} = 0.29 = \frac{\sigma_{Ni-57}}{\sigma_{Se-79}}[/math]

[math]\frac{N_{Se-79}}{N_{Ni-57}} = \left ( \frac{\sigma_{Se-79}}{\sigma_{Ni-57} }\right ) \left ( \frac{\lambda_{Ni-57}}{\lambda_{Se-79}}\right ) = \left ( \frac{1003.92}{214.047} \right ) \left ( \frac{0.0041}{327000} \right ) [/math]

Segebade has a table of ratios of specific activities of certain elements compared to Ni-57. The section starts on page 167, but the ratios with selenium are found on page 176

File:Ch5a PAA SWL 1988.pdf

Chlorine

It looks like Cl-35 is abundant as you see photon energies of 146 keV and 2127 keV (you can barely see 1176 keV) from Cl-34's decay (neutron knocked out of Cl-35).

The half life is 32 minutes.

Should check the half life from the run AccOnAlInDetASe-AinDetD_001.root using the calibration 

MPA->Draw("0.18063+0.960133*evt.Chan>> SeRun_008(8000,0.5,8000.5)","evt.ADCid==3");

Irradiation of Horse Mineral Supplement

Below is the EMSL report for the horse feed sample. https://wiki.iac.isu.edu/index.php/File:EMSL_Report_Horse_Feed.pdf

Chlorine is a dominant signal

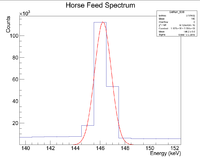
First, look at the peak around 146 keV 146 keV.png

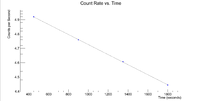
Next I plotted the counts as a function of time to get an exponentially decaying graph. When doing an exponential fit here, the parameter "b" given by root will be the decay constant.

Chlorine.png

Root gives a half life of 32.9508 +/- 0.01 minutes


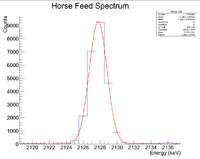
Now do the same for the 2127 keV line 2127 keV.png

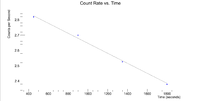
Here are the counts plotted as a function of time 2127.png

Root gives a half life of 35.3962 +/- 0.2 minutes

Potassium is a potential signal

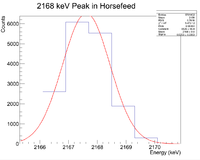
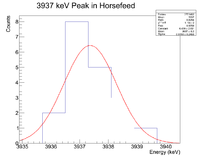
Looking at the spectrum for the fast irradiation sample, there are 2 prominent lines that could be from 38-K. The mechanism would be a single neutron knockout from a stable 39-K nucleus. The two most dominant energies of the three for 38-K are 2167 keV and 3936 keV and the half life is 7.63 minutes. Below is a fit to the energy spectrum histogram

2168 peak.png

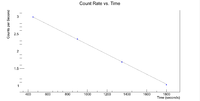
Now check the half life


2167.png

Root gives a half life of 8.03 +/- 0.02 minutes

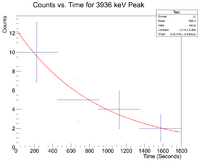
Next check the 3936 peak

3937 Peak.png

and check the half life

3936 keV halflife.png

Root gives a value for b = - 1.14372x10^(-3), which in turn gives a half life of 10.1 minutes

It seems very possible that 38-K could be in the sample of horse feed.

First Observation of Se lines

Using the 44 Machine at 7 kW power and 44 meV incident electron energy to produce a bremsstrahlung spectrum with a mean energy of 15 meV. 


All runs lasting less than 214 seconds have time stamp that gives real time if you divide by clock frequency of 20 MHz.  The first 32 bits are used for a real time measurement.


MDA and Se mass Calculations

To find the mass of the selenium in the irradiated horse feed sample, we need some masses and volumes of the horse feed. A vial containing 20mL of regular horse feed was massed. The mass of the vial was 13.6406g and the total mass of the vial and the horse feed was 31.8504g. This means the mass of the horse feed is [math]31.8504g - 13.6406g = 18.2098g[/math]. Since this mass is in a 20mL = 0.02L container, the density of the horse feed (assuming the mass difference between the non-irradiated and the irradiated horse feed is negligible) is 

[math]\frac{18.2098g}{0.02L} = 910.49 \frac{g}{L}[/math].

Now for the irradiated horse feed the mass of the container is 25.0259g and the total mass of the container and the sample is 43.7529g. The mass of the sample then is 43.7529g - 25.0259g = 18.727g. Now using the density found before we can find the volume of the irradiated horse feed within the container. 

[math]\rho = 910.49\frac{g}{L} = \frac{18.727}{V},  V = \frac{18.727g}{910.49 \frac {g}{L}} = 0.0206L.[/math]

The EMSL report says that there are [math]0.56\frac{mg}{L}[/math] in the horse feed, so the mass of the selenium in the horse feed sample is

[math]0.56\frac{mg}{L}\times 0.0206L = 0.011536mg[/math].


Each of the calibration runs were used at position C in detector D. Below is the runlist for the isotopes used. The intervals used were (117:127) and (272:282) respectively.

Source Serial # Reference Date Activity Start Stop Live
Co-57 129735 07/01/08 1.074 micro Ci 16:17:37 16:27 601.10
Ba-133 129790 07/01/08 1.188 micro Ci 16:29:14 16:32 208.259

For the Co-57, the activity as of 09/07/16 is 0.0005 microCi and the intensity of the 122.3 keV line is 85.6%

= [math]\left (0.856 \right )\left ( 0.0005 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 15.84 Hz [/math] for the 122.3 line


For the Ba-133, the activity as of 09/07/16 is 0.69 microCi and the intensity of the 277.05 keV line is 7.164%

= [math]\left (0.07164 \right )\left ( 0.69 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 1828.97 Hz [/math] for the 277.05 line


Run Source Energy (keV) Expected Rate (Hz) HpGe Rate (Hz) HpGe Det D Efficiency (%)
Eff_C_Co_57.root Co-57 122.3 15.84 0.4526 - 0.2144 1.5
Eff_C_Ba_133.root Ba-133 277.05 1828.97 20.58 - 0.07641 1.12

Now that the efficiency has been found, we must find the background rate to find the MDA. To find the background rate I used ROOT and plotted the energy spectra for Se_B_005 and HorseFeed_NoIrr. The windows of interest are the same as above. Each run's time was cut down to 1 hour.

First I will find the MDA for the window from (117:127). In Se_B_005, the activity was found to be 0.8433 HZ and in the HorseFeed_NoIrr the activity was found to be 0.2133 Hz, which gives a background rate of 0.63 Hz -> 37.6 cpm.

Now we can compute the MDA using this reference https://wiki.iac.isu.edu/index.php/File:Nwsltr-43re.pdf

I found the MDA to be [(2.71 + 4.65*(37.6 * 60)^1/2]/(60*0.015) = 249.1 dpm

Now I will find the MDA for the window from (272:282). In Se_B_005, the activity was found to be 0.7408 Hz and in HorseFeed_NoIrr the activity was found to be 0.08278. This means that the background activity is 0.66 Hz -> 39.48 cpm.

Now we can compute the MDA = [(2.71 + 4.65*(39.48 * 60)^1/2]/(60*0.012) = 318.1 dpm

Detector Efficiency

Below is the runlist for finding the efficiency of the detector at position R


Source Serial # Reference Date Activity Start Stop Live
Na-22 129743 7-01-08 9.427 microCi 15:49 16:19 1796.803
Cs-137 129793 7-01-08 1.006 microCi 14:25 14:56 1879.606
Mn-54 129807 7-01-08 11.77 microCi 15:00 15:30 1793.420
Co-60 129740 7-01-08 10.42 microCi 15:33 15:43 569.725

Below are the theoretical calculations for the theoretical decay frequencies

Na-22, 9.427micro Ci on July 1, 2008, half life 2.602 +/- 0.002 years, 99.937% for 1274.52 and 178.8 for 511 line , activity in March 31, 2016 =1.196micro Ci

= [math]\left (0.99937 \right )\left ( 1.196 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 44,224 Hz [/math] for the 1274 line
= [math]\left (1.788 \right )\left ( 1.196 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 79122.6 Hz [/math] for the 511 line

Cs-137, 661.660 line, 85.21% * 1.066micro Ci on July 1, 2008, half life 30.0 +/- 0.2 yrs, March 31, 2016 activity = 0.891micro Ci expected rate for 661 line

= [math]\left (0.8521 \right )\left ( 0.891 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 28091.2 Hz [/math]

Mn-54, 11.77 microCi on July 1, 2008, half life =312.20 +/- 0.07 days, 99.975% intensity on 834.826 , March 31, 2016 activity =0.02328micro Ci

= [math]\left (0.99975 \right )\left ( 0.02328 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 861.1 Hz [/math] for the 834 line


Co-60, 10.42micro Ci July 1, 2008, half life 5.271 +/- 0.001 years, 99.0 % for 1173.237 and 99.9824 % for 1332.501, March 31, 2016 activity=3.759micro Ci


= [math]\left (0.99 \right )\left ( 3.759 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 137692.17 Hz [/math] for the 1173 line


= [math]\left (0.999824 \right )\left ( 3.759 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 139058.52 Hz [/math] for the 1332 line


Below is a table where the actual efficiency will be calculated for position R (farthest position).

Run Source Energy (keV) Expected Rate (Hz) HpGe Rate (Hz) HpGe Det D Efficiency (%)
Eff_003 Na-22 511 79122.6 (506:516) (4.309-0.065=4.244) 0.005
Eff_005 Cs-137 661.657 28091.2 (657:666)(1.105-0.02281=1.0821) 0.004
Eff_006 Mn-54 834.848 861.1 (830:839)(0.04037-0.009123=0.031247) 0.004
Eff_007 Co-60 1173.228 137692 (1164:1182)(3.686-0.01939=3.67) 0.003
Eff_003 Na-22 1274.537 44224 (1270:1279) (1.073-0.0057=1.0673) 0.002
Eff_007 Co-60 1332.492 139058.52 (1328:1337)(3.283-0.05702=3.22598) 0.002

Below is a runlist for position k

Source Serial # Reference Date Activity Start Stop Live
Na-22 129743 7-01-08 9.427 microCi 14:54 15:01 434.087
Cs-137 129793 7-01-08 1.006 microCi 15:48 15:55 413.925
Mn-54 129807 7-01-08 11.77 microCi 15:28 15:40 705.186
Co-60 129740 7-01-08 10.42 microCi 15:41 15:47 346.092

Below are the theoretical decay frequencies

Na-22, 9.427micro Ci on July 1, 2008, half life 2.602 +/- 0.002 years, 99.937% for 1274.52 and 178.8 for 511 line , activity in April 14, 2016 =1.183micro Ci

= [math]\left (0.99937 \right )\left ( 1.183 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 43743.4 Hz [/math] for the 1274 line
= [math]\left (1.788 \right )\left ( 1.183 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 78262.5 Hz [/math] for the 511 line

Cs-137, 661.660 line, 85.21% * 1.066micro Ci on July 1, 2008, half life 30.0 +/- 0.2 yrs, April 14, 2016 activity =0.890 micro Ci expected rate for 661 line

= [math]\left (0.8521 \right )\left ( 0.890 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 28059.7 Hz [/math]

Mn-54, 11.77 on July 1, 2008, half life =312.20 +/- 0.07 days, 99.975% intensity on 834.826 , April 14, 2016 activity =0.02251micro Ci

= [math]\left (0.99975 \right )\left ( 0.02251 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 830.79 Hz [/math] for the 834 line


Co-60, 10.42micro Ci July 1, 2008, half life 5.271 +/- 0.001 years, 99.0 % for 1173.237 and 99.9824 % for 1332.501, April 14, 2016 activity=3.74micro Ci


= [math]\left (0.99 \right )\left ( 3.74 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 136996.2 Hz [/math] for the 1173 line


= [math]\left (0.999824 \right )\left ( 3.74 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 138355.6 Hz [/math] for the 1332 line

Below are the actual efficiencies for position k

Run Source Energy (keV) Expected Rate (Hz) HpGe Rate (Hz) HpGe Det D Efficiency (%)
Eff_k_002 Na-22 511 79122.6 (506:516)(49.21-0.6272=48.58) 0.06
Eff_k_006 Cs-137 661.657 28091.2 (657:666)(12.86-0.02281=12.837) 0.05
Eff_k_004 Mn-54 834.848 861.1 (830:839)(0.3204-0.009123=0.311) 0.04
Eff_k_005 Co-60 1173.228 137692 (1164:1182)(42.39-0.02053=42.369) 0.03
Eff_k_002 Na-22 1274.537 44224 (1270:1279) (12.53-0.005702)=12.52 0.03
Eff_k_005 Co-60 1332.492 139058.52 (1328:1337)(35.94-0.005072) 0.03

Below is a runlist for position C

Source Serial # Reference Date Activity Start Stop Live
Na-22 129742 7-01-08 1.146 microCi 12:55 12:57 129.782
Cs-137 129793 7-01-08 1.006 microCi 13:02 13:04 123.818
Mn-54 129806 7-01-08 1.226 microCi 13:11 13:21 613.754
Co-60 129739 7-01-08 1.082 microCi 13:08 13:09 103.599

Below are the calculations for the theoretical frequencies

Na-22, 9.427micro Ci on July 1, 2008, half life 2.602 +/- 0.002 years, 99.937% for 1274.52 and 178.8 for 511 line , activity in May 5, 2016 =1.196micro Ci

= [math]\left (0.99937 \right )\left ( 0.14 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 5176.7 Hz [/math] for the 1274 line
= [math]\left (1.788 \right )\left ( 0.14 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 9261.8 Hz [/math] for the 511 line

Cs-137, 661.660 line, 85.21% * 1.066micro Ci on July 1, 2008, half life 30.0 +/- 0.2 yrs, May 5, 2016 activity = 0.89micro Ci expected rate for 661 line

= [math]\left (0.8521 \right )\left ( 0.891 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 28059.7 Hz [/math]

Mn-54, 1.226 microCi on July 1, 2008, half life =312.20 +/- 0.07 days, 99.975% intensity on 834.826 , May 5, 2016 activity =0.002micro Ci

= [math]\left (0.99975 \right )\left ( 0.002 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 73.98 Hz [/math] for the 834 line


Co-60, 1.082micro Ci July 1, 2008, half life 5.271 +/- 0.001 years, 99.0 % for 1173.237 and 99.9824 % for 1332.501, May 5, 2016 activity=0.39micro Ci


= [math]\left (0.99 \right )\left ( 0.39 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 14285.7 Hz [/math] for the 1173 line


= [math]\left (0.999824 \right )\left ( 0.39 \times 10^{-6} \mbox{Ci} \right) \left (\frac{ (3.7 \times 10^{10} \mbox{Hz}}{\mbox{Ci}} \right)= 14427.5 Hz [/math] for the 1332 line

Below is a table with the calculated efficiencies

Run Source Energy (keV) Expected Rate (Hz) HpGe Rate (Hz) HpGe Det D Efficiency (%)
Eff_C_001 Na-22 511 9261.8 (506:516) (45.65-0.065=45.585) 0.5
Eff_C_002 Cs-137 661.657 28059.7 (657:666)(101.7-0.02281=101.67) 0.4
Eff_C_004 Mn-54 834.848 73.98 (830:839)(0.2704-0.009123=0.2612) 0.4
Eff_C_003 Co-60 1173 14285.7 (1164:1182)(34.24-0.01939=34.22) 0.2
Eff_C_001 Na-22 1274.537 5176.7 (1270:1279) (11.15-0.0057=11.14) 0.2
Eff_C_003 Co-60 1332.492 14427.5 (1328:1337)(28.05-0.05702=27.99) 0.2

Run List

Date Time elapsed (Seconds) Sample Document Title Start Stop Real Live Position
04-01-16 2.16x10^6 Se_B Se_B_002 15:55 09:15 235989.882 235687.660 k
04-06-16 2.592x10^6 Se_B Se_B_003 12:57 Interrupted computer crash k
04-14-16 3.283x10^6 Se_B Se_B_005 15:57 09:37 63581.784 63509.895 k
04-15-16 3.37x10^6 Sample D Sample_D_001 14:47 08:23 236172.264 236173.271 k
04-19-16 3.715x10^6 Sample B Sample_B_001 15:31 15:18 85634.862 85624.090 k
4-20-16 3.802x10^6 Sample C Sample_C_001 15:22 10:19 68253.774 68232.238 k
04-21-16 3.888x10^6 Sample A Sample_A_001 10:22 10:37 87292.409 87268.114 k
04-25-16 4.234x10^6 Sample E Sample_E_001 11:36 10:03 80822.406 80795.679 k
04-26-16 4.32x10^6 Se_B Se_B_008 10:06 10:29 87784.755 87664.070 k
05-05-16 5.098x10^6 Sample A Sample_A_002 13:31 14:30 3605.507 3602.925 c
05-05-16 5.098x10^6 Sample B Sample_B_002 14:34 15:26 3114.244 3112.620 c
05-05-16 5.098x10^6 Sample C Sample_C_002 15:28 10:57 70124.788 70044.470 c
05-06-16 5.184x10^6 Sample D Sample_D_002 10:59 15:34 16516.898 16512.570 c
05-06-16 5.184x10^6 Sample E Sample_E_004 15:37 16:18 261654.225 261344.308 c
05-09-16 5.443x10^6 Se B Se_B_012 16:20 11:08 67157.101 66660.298 c
05-10-16 5.5296x10^6 Sample A Sample_A_004 11:03 15:19 15379.475 15363.017 c
05-10-16 5.5296x10^6 Sample B Sample_B_004 15:22:04 11:43 73256.181 73220.324 c
05-16-16 6.048x10^6 Sample C Sample_C_004 16:33 08:19 56758.980 56711.121 c
05-18-16 6.2208x10^6 Sample D Sample_D_006 08:44:21 14:05 19271.829 19266.929 c
05-18-16 6.2208x10^6 Sample E Sample_E_006 14:08 08:06 151108.258 150955.915 c
05-20-16 6.3936x10^6 Se_B Se_B_014 08:08:47 08:44 261353.204 259621.655 c
05-23-16 6.6528x10^6 Sample A Sample_A_006 08:48 13:49 18103.004 18091.523 c
05-23-16 6.6528x10^6 Sample B Sample_B_006 13:52 13:24 84763.938 84696.083 c
05-24-16 6.7392x10^6 Sample C Sample_C_006 13:28:28 10:28 75571.716 75502.871 c
05-31-16 7.344x10^6 Sample B Sample_B_008 08:57:22 08:55 86282.861 86237.392 c
06-01-16 7.4304x10^6 Sample C Sample_C_008 08:58:39 13:31 102739.504 102647.471 c
06-02-16 7.5168x10^6 Sample D Sample_D_010 13:33 08:41 68915.044 68898.246 c

SeRun_01-11-16

SeRun_03-07-16

References

<references/>

File:Krouse CanJournChem 40 1962 p367.pdf

Goryachev, A. M., & Zalesnyy, G. N. (n.d.). The studying of the photoneutron reactions cross sections in the region of the giant dipole resonance in zinc, germanium, selenium, and strontium isotopes. Retrieved September 16, 2016, from http://www-nds.indcentre.org.in/exfor/servlet/X4sSearch5?EntryID=220070

Goryachev, B. I., Ishkhanov, B. S., Kapitonov, I. M., Piskarev, I. M., Piskarev, V. G., & Piskarev, O. P. (n.d.). Giant Dipole Resonance on Ni Isotopes. Retrieved October 26, 2016, from http://www-nds.indcentre.org.in/exfor/servlet/X4sGetSubent?reqx=119235&subID=220597006&plus=1

MSDS

Selenium shot, amorphous, 2-6 mm, Puratronic, 99.999% Alfa Aesar product # 10603 File:AlphaAesarSelenium MDSD.pdf

Informative links

http://www.deq.idaho.gov/regional-offices-issues/pocatello/southeast-idaho-phosphate-mining/southeast-idaho-selenium-investigations/

https://inldigitallibrary.inl.gov/sti/3169894.pdf

http://giscenter.isu.edu/research/Techpg/sisp/index.htm


PAA_Research

Retrieved from "https://wiki.iac.isu.edu/index.php?title=PAA_Selenium&oldid=109782"