Difference between revisions of "Altering Phi Angles"
Jump to navigation
Jump to search
(Created page with "Using the fact that <center><math>\cos{\phi} \equiv \frac{p_x}{\sqrt{p^2-p_z^2}}</math></center> <center><math>\Longrightarrow \sqrt{p^2-p_z^2}=\frac{p_x}{\cos{\phi}}=constant…") |
|||
| Line 22: | Line 22: | ||
<center><math>\Longrightarrow p_y'=\sqrt{p^2-p_z^2-p_x^{'2}}</math></center> | <center><math>\Longrightarrow p_y'=\sqrt{p^2-p_z^2-p_x^{'2}}</math></center> | ||
| + | |||
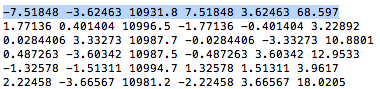
| + | Starting with a data file of momentum components constructed using awk as described above | ||
| + | |||
| + | <center>[[File:Screen_Shot_2016-02-07_at_3.52.37_PM.png | Starting point]]</center> | ||
| + | |||
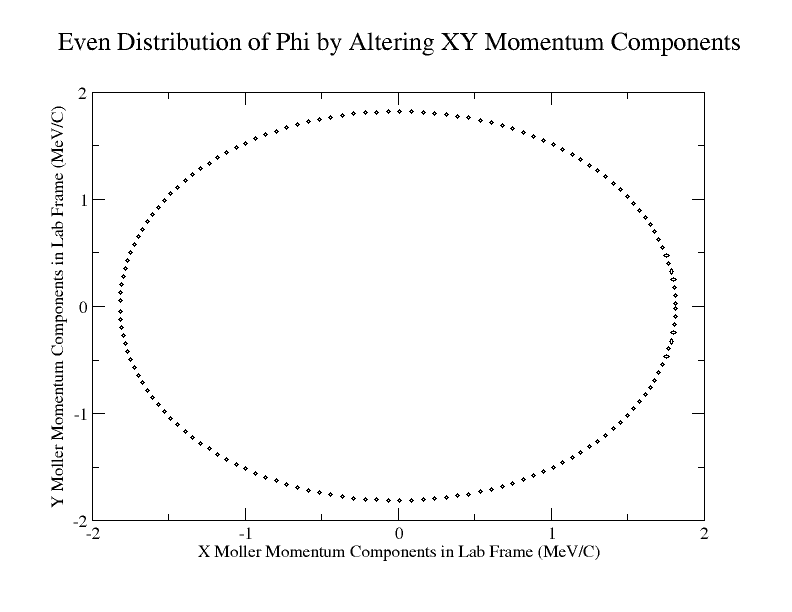
| + | A program was written to rotate the phi angle as described above. The changing x and y components for this distribution can be seen with | ||
| + | |||
| + | <center>[[File:xy.png]]</center> | ||