Difference between revisions of "Forest Relativity Notes"
| (234 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
=Lorentz Transformations= | =Lorentz Transformations= | ||
| + | |||
| + | |||
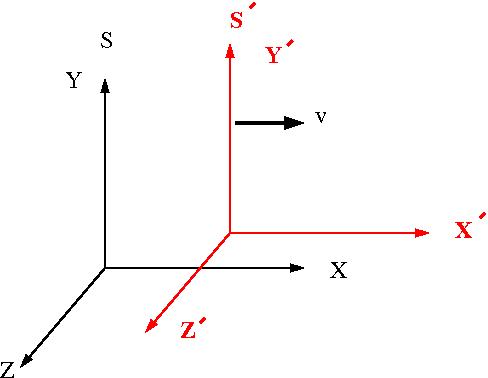
| + | The picture below represents the relative orientation of two different coordinate systems <math>(S, S^{\prime})</math> . <math>S</math> is at rest (Lab Frame) and <math>S^{\prime}</math> is moving at a velocity v to the right with respect to frame <math>S</math>. | ||
| + | |||
| + | [[Image:ForestRelativityLorentzFrame.jpg]] | ||
| + | |||
| + | The relationship between the coordinate<math> (x,y,z,ct)</math> of an object in frame <math>S</math> to the same object described using the coordinates <math>(x^{\prime},y^{\prime},z^{\prime},ct^{\prime})</math> in frame <math>S^{\prime}</math> is geven by the Lorentz transformation: | ||
| + | |||
| + | == Notation== | ||
| + | The relativistic transformation used to transform the coordinates of an object observed in the rest frame <math>S</math> to a moving reference frame<math> S^{\prime}</math> is given by: | ||
:<math>x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}</math> | :<math>x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}</math> | ||
| Line 10: | Line 20: | ||
:<math>x^3\equiv z</math> | :<math>x^3\equiv z</math> | ||
: <math>\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ]</math> | : <math>\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ]</math> | ||
| + | :<math>\beta = \frac{v}{c} = \frac{pc}{E}</math> | ||
| + | : <math>\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}</math> | ||
| + | |||
| + | ;NOTE: It is common in particle physics to define <math> c \equiv 1</math> making <math>\gamma = \frac{E}{m}</math> where <math>m</math> is in units of <math>\frac{\mbox{MeV}}{\mbox{c}^2}</math> | ||
;example | ;example | ||
| Line 18: | Line 32: | ||
:<math>\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )</math> | :<math>\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )</math> | ||
| + | |||
| + | ;Note: Einstein's summation convention drops the <math>\sum</math> symbols and assumes it to exist whenever there is a repeated subscript and uperscript | ||
| + | : ie; <math>x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}</math> | ||
| + | |||
| + | : in the example above the<math> \nu</math> symbol is repeated thereby indicating a summation over <math>\nu</math>. | ||
| + | |||
| + | == Momentum 4-vector == | ||
| + | |||
| + | The momentum 4 -vector is denoted as: | ||
| + | |||
| + | :<math>p^{\mu} \equiv (\frac{E}{c} , \vec{p})</math> | ||
| + | :<math>p_{\mu} \equiv (\frac{E}{c} , -\vec{p})</math> | ||
| + | |||
| + | :<math>p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2</math> | ||
| + | |||
| + | ;Note: There is another convention used for 4-vector notation by Perkins and Koller which goes like this | ||
| + | : <math>p^{\mu} \equiv (\vec{p},iE)</math> | ||
| + | : <math>p_{\mu} \equiv (\vec{p},iE)</math> | ||
| + | |||
| + | == Trig Method== | ||
| + | |||
| + | Another way to represent the Lorentz transformation is by using the substitution | ||
| + | |||
| + | : <math>\sin (\alpha) \equiv \beta \equiv \frac{v}{c}</math> | ||
| + | : <math>\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}</math> | ||
| + | |||
| + | ;The Matrix form of the tranformation looks like | ||
| + | |||
| + | :<math>\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )</math> | ||
| + | |||
| + | ; Or the reverse transformation | ||
| + | |||
| + | :<math>\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )</math> | ||
| + | |||
| + | ;Notice that you just needed to change the signs for the inverse matrix <math>\Lambda^{-1}</math> | ||
| + | |||
| + | =Proper Time and Length= | ||
| + | |||
| + | ==Proper Time== | ||
| + | |||
| + | ;Proper Time <math>\Tau</math> : The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame). | ||
| + | |||
| + | The time given in any frame (t) = <math>\gamma \Tau</math> | ||
| + | |||
| + | ;Note: since <math>\gamma > 1</math> you expect the Proper time interval to be the smallest | ||
| + | |||
| + | == Proper Length== | ||
| + | |||
| + | ; Proper Length<math> (c\Tau)</math>: The length of an object in the object's rest frame. | ||
| + | |||
| + | =Invariant Length= | ||
| + | |||
| + | =Transformation Examples= | ||
| + | |||
| + | |||
| + | == Decay of a Particle at Rest to 2 Bodies== | ||
| + | |||
| + | Consider the decay of the <math>\rho_0</math> meson of mass <math>M</math> at rest into two pions (<math>\pi^+</math> and <math>\pi^-</math> ) of mass <math>m_1</math> and <math>m_2</math> respectively. | ||
| + | |||
| + | |||
| + | [[Image:NeutralRhoMesonDecayDiagram.jpg]] | ||
| + | |||
| + | The diagram above shows a <math>\rho_0</math> meson at rest in the lab which then decays into two pions of momentum <math>p_1</math> and <math>p_2</math> in the center of momentum frame of the <math>\rho_0</math> meson. | ||
| + | |||
| + | Our goal is to determine the momentum and energy of each pion (<math>E_1</math> & <math>E_2</math>) resulting from the decay of the Mother particle. | ||
| + | |||
| + | Conservation of 4-Momentum implies that if <math>P^{\mu}</math> represents the total momentum of the system before the decay then | ||
| + | |||
| + | :<math>P^{\mu} = (E,0) =(M,0) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}</math> | ||
| + | :<math>\Rightarrow 0 = \vec{p}_1 + \vec{p}_2</math> | ||
| + | |||
| + | or | ||
| + | |||
| + | : <math>\vec{p}_1 = - \vec{p}_2</math> | ||
| + | |||
| + | Let | ||
| + | : <math>p \equiv |\vec{p}_1 | = |\vec{p}_2 |</math> | ||
| + | |||
| + | Conservation of Energy | ||
| + | :<math>\Rightarrow E_{tot} = M = E_1 + E_2 = \sqrt{m_1^2 + p^2} + \sqrt{m_2^2 + p^2}</math> | ||
| + | |||
| + | solving for p | ||
| + | |||
| + | :<math>\Rightarrow p = \frac{1}{2M} \sqrt{[M^2 - (m_1-m_2)^2][M^2-(m_1+m_2)^2]}</math> | ||
| + | : <math>\Rightarrow M \ge m_1 + m_2</math> is required to avoid the unphysical condition that the momentum of the particles after a decay would be an imaginary number | ||
| + | |||
| + | Using | ||
| + | |||
| + | :<math>p \equiv |\vec{p}_1 | = |\vec{p}_2 |</math> | ||
| + | : <math>E_1^2 - m_1^2 = E_2^2 - m_2^2</math> | ||
| + | :<math>\Rightarrow E_2 = \sqrt{E_1^2 - m_1^2 + m_2^2}</math> | ||
| + | |||
| + | Combine this with the conservation of energy equation above: | ||
| + | |||
| + | :<math> E_1 + E_2 = E_1 + \sqrt{E_1^2 - m_1^2 + m_2^2} = M</math> | ||
| + | : <math>\Rightarrow E_1 - M = \sqrt{E_1^2 - m_1^2 + m_2^2}</math> | ||
| + | |||
| + | Square both sides of the above equation | ||
| + | |||
| + | : <math>E_1^2 -2ME_1 + M^2 = E_1^2- m_1^2 + m_2^2</math> | ||
| + | :<math>\Rightarrow E_1 = \frac{M^2+m_1^2-m_2^2}{2M}</math> | ||
| + | |||
| + | Similarly | ||
| + | |||
| + | :<math> E_2 = \frac{M^2+m_2^2-m^2_1}{2M}</math> | ||
| + | |||
| + | |||
| + | ;Note: <math>\vec{p}_1 = -\vec{p}_2</math> | ||
| + | :<math>\Rightarrow</math> The daughter particles (pions) from the decay of the Mother particle <math>(\rho)</math> travel in opposite directions with respect to eachother ( ie; they are "back - to -back") | ||
| + | : This means that there is no preferential direction for the decay (the particles are distributed isotropically such that they are back-to-back) | ||
| + | |||
| + | == Decay of Moving Particle to 2 Bodies (decay in flight)== | ||
| + | :<math>P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}</math> | ||
| + | |||
| + | Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles perpendicular to the Z-axis (transverse components:<math>\vec{p}_{1,\perp}</math> and <math>\vec{p}_{2,\perp}</math>) are equal and opposite by conservation of momentum. | ||
| + | |||
| + | :<math>\vec{p}_{1,\perp}\equiv -\vec{p}_{2,\perp}</math> | ||
| + | |||
| + | The center of momentum frame is moving such that | ||
| + | |||
| + | : <math>\beta_{CM} = \frac{p_{tot}}{M}</math> | ||
| + | : <math>\gamma_{CM} = \frac{E_{tot}}{M}</math> | ||
| + | |||
| + | A Lorentz transformation of the kinematics for particle 1 between the Center of Momentum (cm) frame and the lab is given by: | ||
| + | |||
| + | :<math>E_1 = \gamma_{cm}(E_1^{CM} + \beta_{cm}p_{1,z}^{CM})</math> | ||
| + | :<math>p_{1,z} = \gamma_{CM}(p_{1,z}^{CM} + \beta_{cm} E_1^{CM})</math> | ||
| + | :<math>p_{1,\perp} = p_{\perp}^{CM}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>E_1^{CM}</math> = Kinetic Energy (not total) of particle 1 in the center of momentum (CM) reference frame | ||
| + | :<math>p_{1,z}^{CM}</math> = momentum of particle 1 along the direction of the mother particle in the CM frame | ||
| + | :<math>p_{1,\perp}</math> = the component of particle 1's momentum perpendicular to Mother particle's momentum | ||
| + | |||
| + | ;You can now use the results for <math>E_1</math> and <math>p_1=p</math> from the previous section where the Mother particle is at rest to determine the kinematics of the particles in the lab frame given that you know the initial 4-Momentum of the mother particle. You will need to specify the daugher decay angles in the CM frame in order to find the momentum components <math>p_z</math> and <math>p_{\perp}</math>. | ||
| + | |||
| + | ;It can be shown that the lab angle for daughter particle 1 (<math>\theta_1</math>) is given by | ||
| + | :<math>\tan(\theta_1) = \frac{\sin(\theta_1^{CM})}{\gamma_{CM}\left (\frac{\beta_{CM}}{\beta_1^{CM}} + \cos(\theta_1^{CM}) \right )}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>\beta_1^{CM} = \frac{p_1}{E} = \beta</math> for daughter particle 1 in CM frame. | ||
| + | |||
| + | One could also find <math>\vec{p}_1</math> without using the Lorentz transformation. Just use conservation of Energy and Momentum: | ||
| + | |||
| + | :<math>E_{tot} = E_1^{tot} + E_2^{tot} = \sqrt{m_1^2 + p_1^2} + \sqrt{m_2^2 + p_2^2}</math> | ||
| + | : <math>\vec{p_{tot}} = \vec{p}_1 + \vec{p}_2</math> | ||
| + | |||
| + | Solve the conservation of momentum equation for <math>p_2^2</math> | ||
| + | |||
| + | :<math>p_2^2 = (\vec{p_{tot}}- \vec{p}_1)^2 | ||
| + | </math> | ||
| + | |||
| + | and substitute the above for <math>p_2^2</math> in the Conservation of Energy equation above. The dot product gives you the angle between the daughter momentum and the Mother momentum (<math>\theta_1</math>) as a variable. After a lot of algebra you can show that | ||
| + | |||
| + | :<math>p_1 = \frac{\left ( M^2 + m_1^2 -m_2^2 \right ) p_{tot} \cos(\theta_1) \pm 2E\sqrt{M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1)}}{2 \left( M^2 + p^2 \sin^2(\theta_1)\right )}</math> | ||
| + | |||
| + | ;Note: <math>p</math> is the momentum of the two daughter particles in the CM frame which was derived when the Mother particle was at rest. <math>p_{tot}</math> is the momentum of the Mother particle. | ||
| + | |||
| + | |||
| + | In order for a real solution | ||
| + | |||
| + | :<math>M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1) \ge 0</math> | ||
| + | : <math>\Rightarrow \frac{M p}{m_1 p_{tot}} \ge \sin(\theta_1)</math> | ||
| + | |||
| + | |||
| + | If <math>\frac{M p}{m_1 p_{tot}} > 1</math> then <math>\theta_1</math> can be any angle and the "-" sign possibility in "<math>\pm</math>" is rejected to avoided negative values for <math>p_1</math> when <math>\theta_1</math> > <math>\frac{\pi}{2}</math>. | ||
| + | |||
| + | |||
| + | If <math>\frac{M p}{m_1 p_{tot}} < 1</math> then the maximum emmission angle for daughter 1 is given by | ||
| + | :<math>\sin(\theta_1^{max}) = \frac{M p}{m_1 p_{tot}}</math> | ||
| + | |||
| + | The "<math>\pm</math>" is kept because for each <math>\theta_1 < \theta_1^{max}</math> there are two possible trajectories for daughter particle 1 and as a result 2 trajectories for daughter particle 2. | ||
| + | |||
| + | == Decay of Particle to 3 Bodies (Dalitz plot)== | ||
| + | |||
| + | Now lets consider the case where a Mother particle of mass <math>M</math> decays into 3 daughter particles of masses <math>m_1</math>, <math>m_2</math>, and <math>m_3</math>. The 4-mometum conservation is written as | ||
| + | |||
| + | :<math>P^{\mu} = \left ( p_1 \right )^{\mu} +\left ( p_2 \right )^{\mu} +\left ( p_3 \right )^{\mu}</math> | ||
| + | |||
| + | The following invariants are defined | ||
| + | |||
| + | :<math>s = P_{\mu}P^{\mu} = M^2</math> | ||
| + | :<math>s_1 = \left (P -p_1 \right)_{\mu}\left (P -p_1 \right)^{\mu}=\left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}</math> | ||
| + | :<math>s_2 = \left (P -p_2 \right)_{\mu}\left (P -p_2 \right)^{\mu}=\left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}</math> | ||
| + | :<math>s_3 = \left (P -p_3 \right)_{\mu}\left (P -p_3 \right)^{\mu}=\left (p_1 + p_2 \right)_{\mu}\left (p_1 + p_2 \right)^{\mu}</math> | ||
| + | |||
| + | The invariants <math>s_1</math>, <math>s_2</math> and <math>s_3</math> are not independent (the motivation for what is known as a Dalitz plot). Based on the definitions of these invariants and 4-momentum conversation one can show that | ||
| + | |||
| + | :<math>s_1 + s_2 + s_3 = (P^2 -2Pp_1 +p_1^2) +(P^2 -2Pp_2 +p_2^2) + (P^2 -2Pp_3 +p_3^2)</math> | ||
| + | : <math>=3P^2 -2P(p_1+p_2+p_3) +p_1^2+p_2^2+p_3^2</math> | ||
| + | : <math>=3P^2 -2P^2 +p_1^2+p_2^2+p_3^2</math> | ||
| + | :<math>=P^2 +p_1^2+p_2^2+p_3^2</math> | ||
| + | :<math>=M^2 + m_1^2 + m_2^2 +m_3^2</math> | ||
| + | |||
| + | |||
| + | ;Also Note: <math>\sqrt{s_1}</math> is the invariant mass of a subsystem defined by treating daughter particles 2 and 3 as one object. similar interpretations for <math>\sqrt{s_2}</math> and <math>\sqrt{s_3}</math>. | ||
| + | |||
| + | |||
| + | There are limits to the values of the invariant masses <math>s_1</math> - <math>s_3</math> | ||
| + | |||
| + | In the Center of Momentum system we have the | ||
| + | |||
| + | :<math>s_1 = M^2 +m_1^2 - 2ME_1</math> | ||
| + | |||
| + | because | ||
| + | |||
| + | :<math>E_1 = m_1^2 + p_1^2</math> we expect <math>E_1 \ge m_1</math> | ||
| + | |||
| + | This lead to | ||
| + | |||
| + | :<math>\left . s_1 \right |_{max} = M^2 +m_1^2 - 2M(m_1) = (M-m_1)^2</math> | ||
| + | |||
| + | |||
| + | TO find the minimum value of <math>s_1</math> we evaluate <math>s_1</math> in the rest frame of the <math>m_2</math>, <math>m_3</math> subsystem. | ||
| + | |||
| + | :<math>s_1 = \left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}= (E_2^{cm2-3} +E_3^{cm2-3})^2 > (m_2 + m_3)^2</math> : In the CM frame <math>E = \sqrt{p^2 +m^2} = m</math> | ||
| + | |||
| + | so the limits of s_1 are | ||
| + | |||
| + | : <math>(m_2 + m_3)^2 \le s_1 \le (M-m_1)^2</math> | ||
| + | |||
| + | === Invariant mass Dalitz plot Limits === | ||
| + | |||
| + | Analagously you can show the the Min - Max limits for the <math>s_1</math>, <math>s_2</math>, and <math>s_3</math> invariant masses are given by. | ||
| + | |||
| + | : <math>(m_3 + m_1)^2 \le s_2 \le (M-m_2)^2</math> | ||
| + | : <math>(m_1 + m_2)^2 \le s_3 \le (M-m_3)^2</math> | ||
| + | |||
| + | set theory notation is often used to express the above limits as | ||
| + | |||
| + | :<math>s_1 \in \left [ (m_2 + m_3)^2 , (M-m_1)^2 \right ]</math> | ||
| + | :<math>s_2 \in \left [ (m_3 + m_1)^2 , (M-m_2)^2 \right ]</math> | ||
| + | :<math>s_2 \in \left [ (m_1 + m_2)^2, (M-m_3)^2 \right ]</math> | ||
| + | |||
| + | === Dalitz plot boundary curve equation === | ||
| + | |||
| + | Suppose we wish to plot a curve which describes the depence of s_1 on s_2 (determine s_2 as a function of s_1). This is refered to as a Dalitz plot in which <math>s_2</math> appears on the x-axis (abscissa) and <math>s_1</math> appears on the y-axis (ordinate). Becuase of the "squares" in the invariant mass, we can have two values of <math>s_2</math> for a given value of <math>s_1</math>. | ||
| + | |||
| + | since | ||
| + | |||
| + | :<math>s_2 = \left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}</math> | ||
| + | |||
| + | We should look seek equations for <math>p_1</math> and <math>p_3</math> in terms of masses<math>(M,m_1,m_2,m_3)</math> and invariants <math>(s,s_1)</math>. | ||
| + | |||
| + | In order to find such expressions lets consider the problem as viewed by a reference frame in which <math>\vec{p}_3</math> = -<math>\vec{p}_2</math>. This reference frame is sometimes referred to as the Jackson Frame (JF). | ||
| + | |||
| + | In the JF frame | ||
| + | |||
| + | :<math>\vec{P}^{JF} = \vec{p}_1^{JF}</math> : because the other two particles cancel the total momentum of the system is carried by <math>m_1</math>. | ||
| + | |||
| + | :<math>s_1 \equiv = \left (P -p_1 \right)_{\mu}\left (P -p_1 \right)^{\mu}</math> | ||
| + | :<math>=\left [ (E,-\vec{P}) - (E_1,-\vec{p_1})\right ]\left [ (E,\vec{P}) - (E_1,\vec{p}_1)\right ]</math> | ||
| + | :<math>=\left [ (E^{JF},-\vec{P}^{JF}) - (E_1^{JF},-\vec{p}_1^{JF})\right ]\left [ (E^{JF},\vec{P}^{JF}) - (E_1^{JF},\vec{p}_1^{JF})\right ]</math> | ||
| + | : <math>= (E^{JF}-E_1^{JF})^2 : \vec{P}^{JF}=\vec{p}_1^{JF}</math> | ||
| + | :=<math>\left( \sqrt{M^2+(P^{JF})^2} - \sqrt{m^2+(p_1^{JF})^2}\right)</math> : Def of <math>E_{tot}</math> | ||
| + | :=<math>\left( \sqrt{M^2+(p_1^{JF})^2} - \sqrt{m^2+(p_1^{JF})^2}\right)</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>E^{JF}</math> = total energy of Mother particle before it decays | ||
| + | :<math>E_1^{JF}</math> = total energy of <math>m_1</math> particle | ||
| + | |||
| + | solving for <math>p_1^{JF}</math> | ||
| + | |||
| + | :<math>\left( p_1^{JF}\right )^2 = \frac{1}{4s_1} \left [ s_1 -(M-m_1)^2\right ]\left [ s_1 -(M+m_1)^2\right ]</math> | ||
| + | |||
| + | |||
| + | The function <math>\lambda</math> is defined such that | ||
| + | |||
| + | :<math>\lambda(A,B^2,C^2) = \left [ A -(B-C)^2\right ]\left [ A -(B+C)^2\right ]</math> : notice the "squared" arguments | ||
| + | :<math>=A^2 + B^2 + C^2 -2AB -2BC -2CA | ||
| + | </math> | ||
| + | since this solution above is so common in relativistic kinematics | ||
| + | |||
| + | :<math>\Rightarrow \left( p_1^{JF}\right )^2 = \frac{1}{4s_1}\lambda(s_1,M^2,m_1^2) | ||
| + | </math> | ||
| + | |||
| + | Doing an analogous calculation for the other form os s_1 | ||
| + | |||
| + | :<math>s_1 =\left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}</math> | ||
| + | |||
| + | we will find | ||
| + | |||
| + | : <math>p_2^{JF} = p_3^{JF} = \frac{1}{4s_1}\lambda(s_1,m^2,m_3^2)</math> | ||
| + | |||
| + | Lets substitute <math>p_1</math> and <math>p_3</math> into the definition for <math>s_2</math> in the Jackson Frame. | ||
| + | |||
| + | :<math>s_2 = \left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}</math> | ||
| + | :<math>=\left (p_3^{JF} + p_1^{JF} \right)_{\mu}\left (p_3^{JF} + p_1^{JF} \right)^{\mu}</math> | ||
| + | :<math>=\left [ (E_1^{JF},-\vec{p}_1^{JF}) + (E_3^{JF},-\vec{p}_3^{JF})\right]\left [ (E_1^{JF},\vec{p}_1^{JF}) + (E_3^{JF},\vec{p}_3^{JF})\right]</math> | ||
| + | :<math>= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} - p_1^{JF} p_2^{JF} \cos(\theta_{13})\right )</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>\cos(\theta_{13})</math> = angle between <math>\vec{p}_1^{JF}</math> and <math>\vec{p}_3^{JF}</math> | ||
| + | |||
| + | <math>p_1^{JF}</math> and <math>p_2^{JF}</math> are given above we just need to figure out what <math>E_1^{JF}</math> and <math>E_2^{JF}</math> are | ||
| + | |||
| + | |||
| + | If we assume <math>s_1</math> is fixed (you generate the Dalitz plot boundary by determining the two values of <math>s_2</math> for a given value of <math>s_1</math>) then | ||
| + | |||
| + | :<math>E_1^{JF} = \frac{1}{2\sqrt{s_1}} (M^2 - s_1 -m_1^2)</math> | ||
| + | :<math>E_3^{JF} = \frac{1}{2\sqrt{s_1}} (s_1 + m_3^2 -m_2^2) | ||
| + | </math> | ||
| + | |||
| + | The only remaining unkown is the angle <math>(\alpha)</math> between math>\vec{p}_1^{JF}</math> and <math>\vec{p}_3^{JF}</math> which we can treat as either <math>\pi</math> or 0 to determine the min and max values of s_2 for a given value of 2_1. | ||
| + | |||
| + | :<math>s_2= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} - p_1^{JF} p_2^{JF} \cos(\theta_{13})\right )</math> | ||
| + | :<math>= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} \pm p_1^{JF} p_2^{JF} \right )</math> | ||
| + | :<math>= m_1^2 +m_3^2 + 2\left ( \frac{1}{2\sqrt{s_1}} (M^2 - s_1 -m_1^2) \frac{1}{2\sqrt{s_1}} (s_1 + m_3^2 -m_2^2) \pm p_1^{JF} p_2^{JF} \right )</math> | ||
| + | |||
| + | Substituting for <math>p_1^{JF}</math> and <math>p_2^{JF}</math> | ||
| + | :<math>s_2=m_1^2 +m_3^2 + \frac{1}{s_1} \left ((M^2 - s_1 -m_1^2)(s_1 + m_3^2 -m_2^2) \pm \sqrt{\lambda(s_1,M^2,m_1^2) \lambda(s_1,m_2^2,m_3^2)}\right )</math> | ||
| + | |||
| + | The above equation for <math>s_2</math> defines a boundary line of the Dalitz plot. The kinematics of the particles in constrained to the interior of this bounding. | ||
| + | |||
| + | ===Example:<math> D_s^+</math> Meson decay=== | ||
| + | |||
| + | Consider the <math>D_s^+</math> meson which decays <math>\sim</math> 5\% of the time into three particles; <math>K^+K^-\pi^+</math> | ||
| + | |||
| + | :<math>M =1969 MeV</math> for a<math> D_s^+</math> Meson | ||
| + | :<math>m_1 = 494 MeV</math> for a <math> K^+</math> | ||
| + | :<math> m_2 = 140 MeV</math> is a <math>\pi^+</math> | ||
| + | :<math> m_3=494 MeV</math> is a <math>K^-</math> | ||
| + | |||
| + | |||
| + | Dalitz Plot limits are: | ||
| + | |||
| + | :X-axis<math> (s_2)</math> | ||
| + | :Min = <math>(m_3 + m_1)^2 = (988 MeV)^2 \; \sim 1 GeV^2</math> | ||
| + | :Max = <math>(M-m_2)^2 = (1829 MeV)^2 = 3.35 GeV^2</math> | ||
| + | |||
| + | :Y-axis <math>(s_1)</math> | ||
| + | :Min <math>(m_2+m_3)^2 \; \sim (634 MeV)^2 = 0.402 GeV^2</math> | ||
| + | :Max= <math>(M-m_1)^2 = (1475 MeV)^2 = 2.2 GeV^2</math> | ||
| + | |||
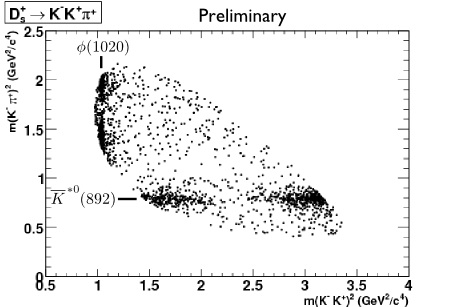
| + | The image below is from experiment E698 | ||
| + | |||
| + | [[Image:DalitzPlot_Dsplus-to-KKPi.jpg]] | ||
| + | |||
| + | Notice the dark bands which have been labeled <math>\phi(1020)</math> and <math>\bar{K}^{*0}(892)</math>. These dark bands indicate a tendency for the decay to clump into states with specific masses, namely <math>s_2=1.04 GeV^2 (\Rightarrow m=1020 MeV)</math> and <math>s_1=0.796 GeV^2 (\Rightarrow m= 892 MeV^2)</math>. The isobar model suggests that the <math>D_s^+</math> decays into two particles and then a third particle. In one case the decay is | ||
| + | |||
| + | :<math>D_s^+ \rightarrow \phi^0 + \pi^+</math> | ||
| + | |||
| + | and then the <math>\phi</math> decays via | ||
| + | |||
| + | :<math>\phi^0 \rightarrow K^+ + K^-</math> | ||
| + | |||
| + | Notice that the dark bands are not infinitely thin but have widths as well. The uncertainty principle (<math>\Delta E \Delta t > \hbar</math>) suggest that only a particle with an infinite lifetime can have a finite , well defined, mass. The width of these dark bands can be used to determine the lifetimes of the intermediate <math>\phi</math> and <math>\bar{K}^{*0}</math> states. | ||
| + | |||
| + | Also notice that there are 2 "clumps" of darks spots in each dark band. The limits for <math>s_2</math> where based on Min/Max values of the <math>\cos(\theta_{13})</math> term. This term tells us how aligned or misaligned the momentum vecors of <math>m_1</math> and <math>m_3</math> (the Kaons)are. | ||
| + | |||
| + | == Elastic Scattering== | ||
| + | |||
| + | [[Image:ForestRelativity_ElasticScateringDiagram.jpg]] | ||
| + | |||
| + | |||
| + | Given the elastic scattering of 2 particles such that the following properties are | ||
| + | |||
| + | ;Known | ||
| + | : <math>m_1</math> = mass of the incident particle #1 | ||
| + | :<math>m_2</math> = mass of the target particle (at rest) #2 | ||
| + | : <math>p_1</math> = momentum of the incident particle #1 | ||
| + | :<math>\theta_1</math> = scattering angle of particle #1 | ||
| + | |||
| + | You can show that | ||
| + | |||
| + | :<math>p_1^{\prime} = \frac{-B \pm \sqrt{B^2 -4AC}}{2A}</math> = Final momentum of scattered particle #1 | ||
| + | :<math>p_2^{\prime} = \left ( p_1^{\prime} \right )^2 -2p_1p_1^{\prime}\cos(\theta_1) + p_1^2</math> = Final momentum of the target particle | ||
| + | : <math>\sin (\theta_2) = - \frac{p_1^{\prime} \sin(\theta_1)}{p_2^{\prime}}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>A = \left ( \sqrt{p_1^2 +m_1^2} +m_2 \right )^2 -p_1^2 \cos^2(\theta_1)</math> | ||
| + | :<math>B = -2p_1 \cos(\theta_1) \left ( m_1^2 + m_2 \sqrt{p_1^2 + m_1^2}\right )</math> | ||
| + | :<math>C = - \left [ m_1^4 + (m_2^2 -m_1^2)(p_1^2 + m_1^2) -m_1^2m_2^2\right ]</math> | ||
| + | |||
| + | == In-Elastic Scattering== | ||
| + | |||
| + | [[Image:ForestRelativity_InelasticScatDiagram.jpg]] | ||
| + | |||
| + | ;List of 4-vectors | ||
| + | :<math>q^{\mu} \equiv ( \omega , \vec{q} )</math> = momentum transfered from incident particle to target | ||
| + | :<math>k_i^{\mu} \equiv (E_i, \vec{k}_i )</math> = initial momentum of incident particle | ||
| + | :<math>k_f^{\mu} \equiv (E_f, \vec{k}_f )</math> = final momentum of incident particle | ||
| + | |||
| + | |||
| + | |||
| + | : <math>q^{\mu} \equiv k_i^{\mu} - k_f^{\mu}</math> = definition of momentum transfer based on conservation of momentum | ||
| + | === Momentum Transfer Squared <math>(Q^2)</math>=== | ||
| + | |||
| + | The momentum transfer squared is given by | ||
| + | |||
| + | :<math>q_{\mu}q^{\mu} = (E_i - E_f)^2 -(\vec{k}_i - \vec{k}_f ) (\vec{k}_i - \vec{k}_f )</math> | ||
| + | :<math>=(E_i^2 -2E_iE_f +F_f^2) - ( |\vec{k}_i |^2 - 2 |\vec{k}_i| |\vec{k}_f| \cos(\theta) + | k_f |^2)</math> | ||
| + | |||
| + | :<math>E^2 = | \vec{k} |^2 +m^2 </math> | ||
| + | |||
| + | :<math>\Rightarrow q_{\mu}q^{\mu} = \left ( | \vec{k}_i |^2 +m_i^2 - 2 E_i E_f +| \vec{k}_f |^2 +m_f^2\right ) - | \vec{k}_i |^2 - | \vec{k}_f |^2 + 2 | \vec{k}_i | | \vec{k}_f |^2 \cos(\theta)</math> | ||
| + | : <math>= m_i^2 + m_f^2 - 2 E_i E_f + 2| \vec{k}_i | | \vec{k}_f |^2 \cos(\theta) | ||
| + | </math> | ||
| + | |||
| + | |||
| + | In the case of electron scattering | ||
| + | |||
| + | :<math>m_i = m_f</math> | ||
| + | :<math>E_i \sim | \vec{k}_i |</math> | ||
| + | :<math>E_f \sim | \vec{k}_f |</math> | ||
| + | : <math>m \ll E</math> | ||
| + | |||
| + | :<math>\Rightarrow q^2 = -2 | \vec{k}_i | | \vec{k}_f | \left ( 1 - \cos (\theta) \right )</math> | ||
| + | : <math>= -4 | \vec{k}_i | | \vec{k}_f | \sin^2(\frac{\theta}{2}) \equiv -4 E_i E_f \sin^2(\frac{\theta}{2})</math> | ||
| + | |||
| + | if<math> q^2 < 0 \Rightarrow</math> spacelike (scattering) | ||
| + | |||
| + | if <math>q^2 > 0 \Rightarrow</math> timelike (free particle) | ||
| + | |||
| + | The Momentum Transfer squared for scattering is define as <math>Q^2</math> such that | ||
| + | |||
| + | : <math>Q^2 = -q^2</math> | ||
| + | |||
| + | === Missing Mass <math>(W)</math>=== | ||
| + | |||
| + | Consider an inelastic scattering process where the particles have the 4-Momentum vectors defined as | ||
| + | |||
| + | : <math>\left ( p_e^{\mu} \right ) \equiv (E_i, \vec{k}_i)</math> = initial momentum 4-vector of the incident electron | ||
| + | : <math>\left ( p_p^{\mu} \right ) \equiv (M_p, 0)</math> = initial momentum 4-vector of the target proton | ||
| + | : <math>\left ( p_e^{\mu} \right )^{\prime} \equiv (E_f, \vec{k}_f)</math> = final momentum 4-vector of the scattered electron | ||
| + | : <math>\left ( p_p^{\mu} \right )^{\prime} \equiv (E_X, \vec{p}_X)</math> = final momentum 4-vector of the target proton | ||
| + | :<math>W^2 \equiv \left (E_X^2 -p_X^2 \right )</math> = mass of scattered proton | ||
| + | |||
| + | Conservation of 4-Momentum | ||
| + | |||
| + | :<math>\left ( p_e \right )^{\mu} + \left ( p_p \right )^{\mu} = \left ( p_e^{\prime} \right )^{\mu} + \left ( p_p^{\prime} \right )^{\mu}</math> | ||
| + | |||
| + | solve for final proton momentum 4-vector and determine the length | ||
| + | |||
| + | :<math>\left ( p_p^{\prime} \right )_{\mu} \left ( p_p^{\prime} \right )^{\mu} = \left [ \left ( p_e \right )^{\mu} + \left ( p_p \right )^{\mu} - \left ( p_e^{\prime} \right )^{\mu}\right ] \left [ \left ( p_e \right )_{\mu} + \left ( p_p \right )_{\mu} - \left ( p_e^{\prime} \right )_{\mu}\right ] </math> | ||
| + | |||
| + | |||
| + | |||
| + | :<math>W^2 \equiv \left ( p_p^{\prime} \right )_{\mu} \left ( p_p^{\prime} \right )^{\mu}</math> | ||
| + | : = <math>\left [ (E_i, \vec{k}_i) + (M_p, 0) - (E_f, \vec{k}_f) \right ]\left [ \left ( {E_i \atop \vec{k}_i }\right ) + \left ( {M_p \atop 0 }\right ) - \left ( {E_f \atop \vec{k}_f }\right )\right ]</math> | ||
| + | :<math>= (E_i^2 - k_i^2 ) + (E_f^2 - k_f^2 ) + M_p^2 + 2 M_p(E_i - E_f) - 2(E_iE_f - \vec{k}_i \cdot \vec{k}_f )</math> | ||
| + | := <math>m_e^2 + m_e^2 +M_p^2 + 2 M_p(E_i - E_f) - 2(E_iE_f - \vec{k}_i \cdot \vec{k}_f ) | ||
| + | </math> | ||
| + | |||
| + | : <math>q^2= m_i^2 + m_f^2 - 2 E_i E_f + 2| \vec{k}_i | | \vec{k}_f |^2 \cos(\theta)</math> | ||
| + | |||
| + | |||
| + | substitution | ||
| + | |||
| + | :<math>W^2 = M_p^2 + 2M_p (E_i -E_f) + q^2 = M_p^2 + 2 M_p(E_i - E_f) -Q^2</math> | ||
| + | |||
| + | ==Tranform to Center of Mass== | ||
| + | |||
| + | ;A relativistic transformation from a rest frame where <math>E,\vec{p}</math> are given to a frame moving with velocity <math>\beta</math> is given by: | ||
| + | |||
| + | :<math>\left ( \begin{matrix} E^{\prime} \\ p^{\prime}_x \\ p^{\prime}_y \\ p^{\prime}_z \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} E \\ p_x \\ p_y \\ p_z \end{matrix} \right )</math> | ||
| + | |||
| + | |||
| + | The velocity of the center of mass frame for the case of a fixed target scattering event (the target is at rest) is given by | ||
| + | |||
| + | :<math>\vec v_{cm} c = \vec \beta = \frac{\vec{p_1}}{p^0} = \frac{\vec p_1}{E_1+m_2}</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | :<math>E_1,\vec p_1</math> are the energy and momentum for the incident particle | ||
| + | :<math>m_2</math> is the mass of the target particle | ||
| + | |||
| + | :<math>\beta = \frac{v}{c} = \frac{pc}{E}</math> | ||
| + | : <math>\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2} = \frac{E_1 + m_2}{\sqrt{m_1^2+m_2^2+2 E_1m_2}}</math> | ||
| + | |||
| + | |||
| + | Assume an incident electron of 11 GeV moller scatters | ||
| + | |||
| + | :<math>p_1^{\mu} = ( E_1, \vec p_1) = (sqrt{11^2+0.000511^2, 11 \hat i} )= (11.0000000118691,11 \hat i)</math> | ||
| + | :<math>p_2^{\mu} = ( E_2,\vec 0) = (0.000511,0)</math> | ||
| + | |||
| + | :<math>v_{cm} = \frac{m_1 v_1}{m_1+m_2}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ===Using ROOT functions=== | ||
| + | |||
| + | TLorentzVector P1,P2; | ||
| + | |||
| + | |||
| + | set the momentum four vector for an 11 GeV electron | ||
| + | |||
| + | P1.SetPxPyPzE(11,0,0,sqrt(11*11+0.000511*0.000511)) | ||
| + | P2.SetPxPyPzE(0,0,0,0.000511) | ||
| + | Check that you get the mass of the electron in Units of GeV | ||
| + | |||
| + | |||
| + | The invariant mass of the particle is given by | ||
| + | |||
| + | root [36] P1.Mag() | ||
| + | (const Double_t)5.11000016012715737e-04 | ||
| + | |||
| + | The Beta and Gamma of the Particle are Given by | ||
| + | |||
| + | |||
| + | P1.Beta() | ||
| + | (const Double_t)9.99999998920987565e-01 | ||
| + | root [42] P1.Gamma() | ||
| + | (const Double_t)2.15264184050203912e+04 | ||
| + | |||
| + | |||
| + | The Kinetic Energy (<math>(\gamma-1)m_oc^2</math>) is Given by | ||
| + | |||
| + | root [43] (P1.Gamma()-1)*0.511 | ||
| + | (const double)1.09994888049654201e+04 | ||
| + | root [46] (P1.Gamma()-1)*P1.Mag() | ||
| + | (const double)1.09994891496458251e+01 | ||
| + | |||
| + | |||
| + | assume you moller scatter off a free electron at rest. | ||
| + | |||
| + | Construct the boost vector | ||
| + | |||
| + | |||
| + | TLorentzVector CMS; | ||
| + | |||
| + | CMS=P1+P2; | ||
| + | |||
| + | P1.Boost(-CMS.BoostVector()); | ||
| + | P2.Boost(-CMS.BoostVector()); | ||
| + | |||
| + | root [138] P1.Px() | ||
| + | (const Double_t)5.30129176950140391e-02 | ||
| + | root [139] P2.Px() | ||
| + | (const Double_t)(-5.30129176949399178e-02) | ||
| + | |||
| + | A final state moller scattering event from GEANT4 has | ||
| + | |||
| + | The scattered electron | ||
| + | |||
| + | P3.SetPxPyPzE(0.433025,-0.858867,10999.6,sqrt(0.433025*0.433025+0.858867*0.858867+10999.6*10999.6+ 0.000511*0.000511)) | ||
| + | |||
| + | The moller electron | ||
| + | |||
| + | P4.SetPxPyPzE(-0.433025,0.858867,0.905366,sqrt(0.433025*0.433025+0.858867*0.858867+0.905366*0.905366+ 0.000511*0.000511)) | ||
| + | |||
| + | |||
| + | <pre> | ||
| + | CMS=P3+P4 | ||
| + | |||
| + | |||
| + | P3.Boost(-CMS.BoostVector()); | ||
| + | root [191] P4.Boost(-CMS.BoostVector()); | ||
| + | root [192] P3.Px() | ||
| + | (const Double_t)4.33024999999999993e-01 | ||
| + | root [193] P4.Px() | ||
| + | (const Double_t)(-4.33024999999999993e-01) | ||
| + | root [194] P3.Py() | ||
| + | (const Double_t)(-8.58867000000000047e-01) | ||
| + | root [195] P4.Py() | ||
| + | (const Double_t)8.58867000000000047e-01 | ||
| + | root [196] P3.Pz() | ||
| + | (const Double_t)4.78021531980484724e+01 | ||
| + | root [197] P4.Pz() | ||
| + | (const Double_t)(-4.78021531981362244e+01) | ||
| + | root [198] P3.E() | ||
| + | (const Double_t)4.78118292245973180e+01 | ||
| + | root [199] P4.E() | ||
| + | (const Double_t)4.78118292247171723e+01 | ||
| + | |||
| + | </pre> | ||
| + | |||
| + | |||
| + | [http://iac.isu.edu/mediawiki/index.php/Classes Back to Classes] | ||
Latest revision as of 17:39, 28 April 2015
Lorentz Transformations
The picture below represents the relative orientation of two different coordinate systems . is at rest (Lab Frame) and is moving at a velocity v to the right with respect to frame .
The relationship between the coordinate of an object in frame to the same object described using the coordinates in frame is geven by the Lorentz transformation:
Notation
The relativistic transformation used to transform the coordinates of an object observed in the rest frame to a moving reference frame is given by:
where
- NOTE
- It is common in particle physics to define making where is in units of
- example
- Or in matrix form the tranformation looks like
- Note
- Einstein's summation convention drops the symbols and assumes it to exist whenever there is a repeated subscript and uperscript
- ie;
- in the example above the symbol is repeated thereby indicating a summation over .
Momentum 4-vector
The momentum 4 -vector is denoted as:
- Note
- There is another convention used for 4-vector notation by Perkins and Koller which goes like this
Trig Method
Another way to represent the Lorentz transformation is by using the substitution
- The Matrix form of the tranformation looks like
- Or the reverse transformation
- Notice that you just needed to change the signs for the inverse matrix
Proper Time and Length
Proper Time
- Proper Time
- The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).
The time given in any frame (t) =
- Note
- since you expect the Proper time interval to be the smallest
Proper Length
- Proper Length
- The length of an object in the object's rest frame.
Invariant Length
Transformation Examples
Decay of a Particle at Rest to 2 Bodies
Consider the decay of the meson of mass at rest into two pions ( and ) of mass and respectively.
File:NeutralRhoMesonDecayDiagram.jpg
The diagram above shows a meson at rest in the lab which then decays into two pions of momentum and in the center of momentum frame of the meson.
Our goal is to determine the momentum and energy of each pion ( & ) resulting from the decay of the Mother particle.
Conservation of 4-Momentum implies that if represents the total momentum of the system before the decay then
or
Let
Conservation of Energy
solving for p
- is required to avoid the unphysical condition that the momentum of the particles after a decay would be an imaginary number
Using
Combine this with the conservation of energy equation above:
Square both sides of the above equation
Similarly
- Note
- The daughter particles (pions) from the decay of the Mother particle travel in opposite directions with respect to eachother ( ie; they are "back - to -back")
- This means that there is no preferential direction for the decay (the particles are distributed isotropically such that they are back-to-back)
Decay of Moving Particle to 2 Bodies (decay in flight)
Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles perpendicular to the Z-axis (transverse components: and ) are equal and opposite by conservation of momentum.
The center of momentum frame is moving such that
A Lorentz transformation of the kinematics for particle 1 between the Center of Momentum (cm) frame and the lab is given by:
where
- = Kinetic Energy (not total) of particle 1 in the center of momentum (CM) reference frame
- = momentum of particle 1 along the direction of the mother particle in the CM frame
- = the component of particle 1's momentum perpendicular to Mother particle's momentum
- You can now use the results for and from the previous section where the Mother particle is at rest to determine the kinematics of the particles in the lab frame given that you know the initial 4-Momentum of the mother particle. You will need to specify the daugher decay angles in the CM frame in order to find the momentum components and .
- It can be shown that the lab angle for daughter particle 1 () is given by
where
- for daughter particle 1 in CM frame.
One could also find without using the Lorentz transformation. Just use conservation of Energy and Momentum:
Solve the conservation of momentum equation for
and substitute the above for in the Conservation of Energy equation above. The dot product gives you the angle between the daughter momentum and the Mother momentum () as a variable. After a lot of algebra you can show that
- Note
- is the momentum of the two daughter particles in the CM frame which was derived when the Mother particle was at rest. is the momentum of the Mother particle.
In order for a real solution
If then can be any angle and the "-" sign possibility in "" is rejected to avoided negative values for when > .
If then the maximum emmission angle for daughter 1 is given by
The "" is kept because for each there are two possible trajectories for daughter particle 1 and as a result 2 trajectories for daughter particle 2.
Decay of Particle to 3 Bodies (Dalitz plot)
Now lets consider the case where a Mother particle of mass decays into 3 daughter particles of masses , , and . The 4-mometum conservation is written as
The following invariants are defined
The invariants , and are not independent (the motivation for what is known as a Dalitz plot). Based on the definitions of these invariants and 4-momentum conversation one can show that
- Also Note
- is the invariant mass of a subsystem defined by treating daughter particles 2 and 3 as one object. similar interpretations for and .
There are limits to the values of the invariant masses -
In the Center of Momentum system we have the
because
- we expect
This lead to
TO find the minimum value of we evaluate in the rest frame of the , subsystem.
- : In the CM frame
so the limits of s_1 are
Invariant mass Dalitz plot Limits
Analagously you can show the the Min - Max limits for the , , and invariant masses are given by.
set theory notation is often used to express the above limits as
Dalitz plot boundary curve equation
Suppose we wish to plot a curve which describes the depence of s_1 on s_2 (determine s_2 as a function of s_1). This is refered to as a Dalitz plot in which appears on the x-axis (abscissa) and appears on the y-axis (ordinate). Becuase of the "squares" in the invariant mass, we can have two values of for a given value of .
since
We should look seek equations for and in terms of masses and invariants .
In order to find such expressions lets consider the problem as viewed by a reference frame in which = -. This reference frame is sometimes referred to as the Jackson Frame (JF).
In the JF frame
- : because the other two particles cancel the total momentum of the system is carried by .
- = : Def of
- =
where
- = total energy of Mother particle before it decays
- = total energy of particle
solving for
The function is defined such that
- : notice the "squared" arguments
since this solution above is so common in relativistic kinematics
Doing an analogous calculation for the other form os s_1
we will find
Lets substitute and into the definition for in the Jackson Frame.
where
- = angle between and
and are given above we just need to figure out what and are
If we assume is fixed (you generate the Dalitz plot boundary by determining the two values of for a given value of ) then
The only remaining unkown is the angle between math>\vec{p}_1^{JF}</math> and which we can treat as either or 0 to determine the min and max values of s_2 for a given value of 2_1.
Substituting for and
The above equation for defines a boundary line of the Dalitz plot. The kinematics of the particles in constrained to the interior of this bounding.
Example: Meson decay
Consider the meson which decays 5\% of the time into three particles;
- for a Meson
- for a
- is a
- is a
Dalitz Plot limits are:
- X-axis
- Min =
- Max =
- Y-axis
- Min
- Max=
The image below is from experiment E698
Notice the dark bands which have been labeled and . These dark bands indicate a tendency for the decay to clump into states with specific masses, namely and . The isobar model suggests that the decays into two particles and then a third particle. In one case the decay is
and then the decays via
Notice that the dark bands are not infinitely thin but have widths as well. The uncertainty principle () suggest that only a particle with an infinite lifetime can have a finite , well defined, mass. The width of these dark bands can be used to determine the lifetimes of the intermediate and states.
Also notice that there are 2 "clumps" of darks spots in each dark band. The limits for where based on Min/Max values of the term. This term tells us how aligned or misaligned the momentum vecors of and (the Kaons)are.
Elastic Scattering
File:ForestRelativity ElasticScateringDiagram.jpg
Given the elastic scattering of 2 particles such that the following properties are
- Known
- = mass of the incident particle #1
- = mass of the target particle (at rest) #2
- = momentum of the incident particle #1
- = scattering angle of particle #1
You can show that
- = Final momentum of scattered particle #1
- = Final momentum of the target particle
where
In-Elastic Scattering
File:ForestRelativity InelasticScatDiagram.jpg
- List of 4-vectors
- = momentum transfered from incident particle to target
- = initial momentum of incident particle
- = final momentum of incident particle
- = definition of momentum transfer based on conservation of momentum
Momentum Transfer Squared
The momentum transfer squared is given by
In the case of electron scattering
if spacelike (scattering)
if timelike (free particle)
The Momentum Transfer squared for scattering is define as such that
Missing Mass
Consider an inelastic scattering process where the particles have the 4-Momentum vectors defined as
- = initial momentum 4-vector of the incident electron
- = initial momentum 4-vector of the target proton
- = final momentum 4-vector of the scattered electron
- = final momentum 4-vector of the target proton
- = mass of scattered proton
Conservation of 4-Momentum
solve for final proton momentum 4-vector and determine the length
- =
- =
substitution
Tranform to Center of Mass
- A relativistic transformation from a rest frame where are given to a frame moving with velocity is given by
The velocity of the center of mass frame for the case of a fixed target scattering event (the target is at rest) is given by
where
- are the energy and momentum for the incident particle
- is the mass of the target particle
Assume an incident electron of 11 GeV moller scatters
Using ROOT functions
TLorentzVector P1,P2;
set the momentum four vector for an 11 GeV electron
P1.SetPxPyPzE(11,0,0,sqrt(11*11+0.000511*0.000511)) P2.SetPxPyPzE(0,0,0,0.000511)
Check that you get the mass of the electron in Units of GeV
The invariant mass of the particle is given by
root [36] P1.Mag() (const Double_t)5.11000016012715737e-04
The Beta and Gamma of the Particle are Given by
P1.Beta() (const Double_t)9.99999998920987565e-01 root [42] P1.Gamma() (const Double_t)2.15264184050203912e+04
The Kinetic Energy () is Given by
root [43] (P1.Gamma()-1)*0.511 (const double)1.09994888049654201e+04 root [46] (P1.Gamma()-1)*P1.Mag() (const double)1.09994891496458251e+01
assume you moller scatter off a free electron at rest.
Construct the boost vector
TLorentzVector CMS;
CMS=P1+P2;
P1.Boost(-CMS.BoostVector()); P2.Boost(-CMS.BoostVector());
root [138] P1.Px() (const Double_t)5.30129176950140391e-02 root [139] P2.Px() (const Double_t)(-5.30129176949399178e-02)
A final state moller scattering event from GEANT4 has
The scattered electron
P3.SetPxPyPzE(0.433025,-0.858867,10999.6,sqrt(0.433025*0.433025+0.858867*0.858867+10999.6*10999.6+ 0.000511*0.000511))
The moller electron
P4.SetPxPyPzE(-0.433025,0.858867,0.905366,sqrt(0.433025*0.433025+0.858867*0.858867+0.905366*0.905366+ 0.000511*0.000511))
CMS=P3+P4 P3.Boost(-CMS.BoostVector()); root [191] P4.Boost(-CMS.BoostVector()); root [192] P3.Px() (const Double_t)4.33024999999999993e-01 root [193] P4.Px() (const Double_t)(-4.33024999999999993e-01) root [194] P3.Py() (const Double_t)(-8.58867000000000047e-01) root [195] P4.Py() (const Double_t)8.58867000000000047e-01 root [196] P3.Pz() (const Double_t)4.78021531980484724e+01 root [197] P4.Pz() (const Double_t)(-4.78021531981362244e+01) root [198] P3.E() (const Double_t)4.78118292245973180e+01 root [199] P4.E() (const Double_t)4.78118292247171723e+01