Forest Relativity Notes

Lorentz Transformations

The picture below represents the relative orientation of two different coordinate systems $(S, S^{\prime})$ . $S$ is at rest (Lab Frame) and $S^{\prime}$ is moving at a velocity v to the right with respect to frame $S$.

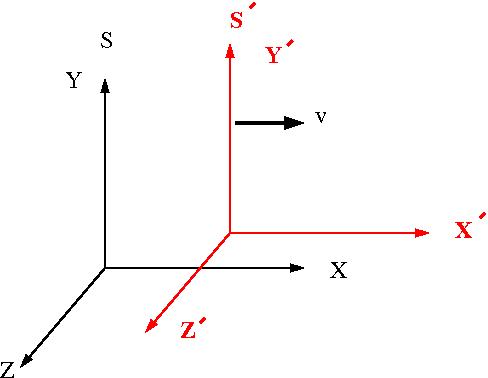
The relationship between the coordinate$(x,y,z,ct)$ of an object in frame $S$ to the same object described using the coordinates $(x^{\prime},y^{\prime},z^{\prime},ct^{\prime})$ in frame $S^{\prime}$ is geven by the Lorentz transformation:

Notation

The relativistic transformation used to transform the coordinates of an object observed in the rest frame $S$ to a moving reference frame$S^{\prime}$ is given by:

$x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}$

where

$x^0 \equiv ct$

$x^1 \equiv x$

$x^2\equiv y$

$x^3\equiv z$

$\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ]$

$\beta = \frac{v}{c} = \frac{pc}{E}$

$\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}$

NOTE

It is common in particle physics to define $c \equiv 1$ making $\gamma = \frac{E}{m}$ where $m$ is in units of $\frac{\mbox{MeV}}{\mbox{c}^2}$

example

$x^{0^{\prime}} = \sum_{\nu=0}^2 \Lambda_{\nu}^0 x^{\nu} = \Lambda_0^0 x^0 + \Lambda_1^0 x^1 \Lambda_2^0 x^2 + \Lambda_3^0 x^2$

$ct^{\prime}= \gamma x^0 - \gamma \beta x^1 + 0 x^2 + 0 x^3 = \gamma ct - \gamma \beta x = \gamma(ct -\beta x)$

Or in matrix form the tranformation looks like

$\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )$

Note

Einstein's summation convention drops the $\sum$ symbols and assumes it to exist whenever there is a repeated subscript and uperscript

ie; $x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}$

in the example above the$\nu$ symbol is repeated thereby indicating a summation over $\nu$.

Momentum 4-vector

The momentum 4 -vector is denoted as:

$p^{\mu} \equiv (\frac{E}{c} , \vec{p})$

$p_{\mu} \equiv (\frac{E}{c} , -\vec{p})$

$p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2$

Note

There is another convention used for 4-vector notation by Perkins and Koller which goes like this

$p^{\mu} \equiv (\vec{p},iE)$

$p_{\mu} \equiv (\vec{p},iE)$

Trig Method

Another way to represent the Lorentz transformation is by using the substitution

$\sin (\alpha) \equiv \beta \equiv \frac{v}{c}$

$\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}$

The Matrix form of the tranformation looks like

$\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )$

Or the reverse transformation

$\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )$

Notice that you just needed to change the signs for the inverse matrix $\Lambda^{-1}$

Proper Time and Length

Proper Time

Proper Time $\Tau$

The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).

The time given in any frame (t) = $\gamma \Tau$

Note

since $\gamma \gt 1$ you expect the Proper time interval to be the smallest

Proper Length

Proper Length$(c\Tau)$

The length of an object in the object's rest frame.

Transformation Examples

Decay of a Particle at Rest to 2 Bodies

Consider the decay of the $\rho_0$ meson of mass $M$ at rest into two pions ($\pi^+$ and $\pi^-$ ) of mass $m_1$ and $m_2$ respectively.

File:NeutralRhoMesonDecayDiagram.jpg

The diagram above shows a $\rho_0$ meson at rest in the lab which then decays into two pions of momentum $p_1$ and $p_2$ in the center of momentum frame of the $\rho_0$ meson.

Our goal is to determine the momentum and energy of each pion ($E_1$ & $E_2$) resulting from the decay of the Mother particle.

Conservation of 4-Momentum implies that if $P^{\mu}$ represents the total momentum of the system before the decay then

$P^{\mu} = (E,0) =(M,0) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}$

$\Rightarrow 0 = \vec{p}_1 + \vec{p}_2$

or

$\vec{p}_1 = - \vec{p}_2$

Let

$p \equiv |\vec{p}_1 | = |\vec{p}_2 |$

Conservation of Energy

$\Rightarrow E_{tot} = M = E_1 + E_2 = \sqrt{m_1^2 + p^2} + \sqrt{m_2^2 + p^2}$

solving for p

$\Rightarrow p = \frac{1}{2M} \sqrt{[M^2 - (m_1-m_2)^2][M^2-(m_1+m_2)^2]}$

$\Rightarrow M \ge m_1 + m_2$ is required to avoid the unphysical condition that the momentum of the particles after a decay would be an imaginary number

Using

$p \equiv |\vec{p}_1 | = |\vec{p}_2 |$

$E_1^2 - m_1^2 = E_2^2 - m_2^2$

$\Rightarrow E_2 = \sqrt{E_1^2 - m_1^2 + m_2^2}$

Combine this with the conservation of energy equation above:

$E_1 + E_2 = E_1 + \sqrt{E_1^2 - m_1^2 + m_2^2} = M$

$\Rightarrow E_1 - M = \sqrt{E_1^2 - m_1^2 + m_2^2}$

Square both sides of the above equation

$E_1^2 -2ME_1 + M^2 = E_1^2- m_1^2 + m_2^2$

$\Rightarrow E_1 = \frac{M^2+m_1^2-m_2^2}{2M}$

Similarly

$E_2 = \frac{M^2+m_2^2-m^2_1}{2M}$

Note

$\vec{p}_1 = -\vec{p}_2$

$\Rightarrow$ The daughter particles (pions) from the decay of the Mother particle $(\rho)$ travel in opposite directions with respect to eachother ( ie; they are "back - to -back")

This means that there is no preferential direction for the decay (the particles are distributed isotropically such that they are back-to-back)

Decay of Moving Particle to 2 Bodies (decay in flight)

$P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}$

Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles perpendicular to the Z-axis (transverse components:$\vec{p}_{1,\perp}$ and $\vec{p}_{2,\perp}$) are equal and opposite by conservation of momentum.

$\vec{p}_{1,\perp}\equiv -\vec{p}_{2,\perp}$

The center of momentum frame is moving such that

$\beta_{CM} = \frac{p_{tot}}{M}$

$\gamma_{CM} = \frac{E_{tot}}{M}$

A Lorentz transformation of the kinematics for particle 1 between the Center of Momentum (cm) frame and the lab is given by:

$E_1 = \gamma_{cm}(E_1^{CM} + \beta_{cm}p_{1,z}^{CM})$

$p_{1,z} = \gamma_{CM}(p_{1,z}^{CM} + \beta_{cm} E_1^{CM})$

$p_{1,\perp} = p_{\perp}^{CM}$

where

$E_1^{CM}$ = Kinetic Energy (not total) of particle 1 in the center of momentum (CM) reference frame

$p_{1,z}^{CM}$ = momentum of particle 1 along the direction of the mother particle in the CM frame

$p_{1,\perp}$ = the component of particle 1's momentum perpendicular to Mother particle's momentum

You can now use the results for $E_1$ and $p_1=p$ from the previous section where the Mother particle is at rest to determine the kinematics of the particles in the lab frame given that you know the initial 4-Momentum of the mother particle. You will need to specify the daugher decay angles in the CM frame in order to find the momentum components $p_z$ and $p_{\perp}$.

It can be shown that the lab angle for daughter particle 1 ($\theta_1$) is given by

$\tan(\theta_1) = \frac{\sin(\theta_1^{CM})}{\gamma_{CM}\left (\frac{\beta_{CM}}{\beta_1^{CM}} + \cos(\theta_1^{CM}) \right )}$

where

$\beta_1^{CM} = \frac{p_1}{E} = \beta$ for daughter particle 1 in CM frame.

One could also find $\vec{p}_1$ without using the Lorentz transformation. Just use conservation of Energy and Momentum:

$E_{tot} = E_1^{tot} + E_2^{tot} = \sqrt{m_1^2 + p_1^2} + \sqrt{m_2^2 + p_2^2}$

$\vec{p_{tot}} = \vec{p}_1 + \vec{p}_2$

Solve the conservation of momentum equation for $p_2^2$

$p_2^2 = (\vec{p_{tot}}- \vec{p}_1)^2$

and substitute the above for $p_2^2$ in the Conservation of Energy equation above. The dot product gives you the angle between the daughter momentum and the Mother momentum ($\theta_1$) as a variable. After a lot of algebra you can show that

$p_1 = \frac{\left ( M^2 + m_1^2 -m_2^2 \right ) p_{tot} \cos(\theta_1) \pm 2E\sqrt{M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1)}}{2 \left( M^2 + p^2 \sin^2(\theta_1)\right )}$

Note

$p$ is the momentum of the two daughter particles in the CM frame which was derived when the Mother particle was at rest. $p_{tot}$ is the momentum of the Mother particle.

In order for a real solution

$M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1) \ge 0$

$\Rightarrow \frac{M p}{m_1 p_{tot}} \ge \sin(\theta_1)$

If $\frac{M p}{m_1 p_{tot}} \gt 1$ then $\theta_1$ can be any angle and the "-" sign possibility in "$\pm$" is rejected to avoided negative values for $p_1$ when $\theta_1$ > $\frac{\pi}{2}$.

If $\frac{M p}{m_1 p_{tot}} \lt 1$ then the maximum emmission angle for daughter 1 is given by

$\sin(\theta_1^{max}) = \frac{M p}{m_1 p_{tot}}$

The "$\pm$" is kept because for each $\theta_1 \lt \theta_1^{max}$ there are two possible trajectories for daughter particle 1 and as a result 2 trajectories for daughter particle 2.

Decay of Particle to 3 Bodies (Dalitz plot)

Now lets consider the case where a Mother particle of mass $M$ decays into 3 daughter particles of masses $m_1$, $m_2$, and $m_3$. The 4-mometum conservation is written as

$P^{\mu} = \left ( p_1 \right )^{\mu} +\left ( p_2 \right )^{\mu} +\left ( p_3 \right )^{\mu}$

The following invariants are defined

$s = P_{\mu}P^{\mu} = M^2$

$s_1 = \left (P -p_1 \right)_{\mu}\left (P -p_1 \right)^{\mu}=\left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}$

$s_2 = \left (P -p_2 \right)_{\mu}\left (P -p_2 \right)^{\mu}=\left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}$

$s_3 = \left (P -p_3 \right)_{\mu}\left (P -p_3 \right)^{\mu}=\left (p_1 + p_2 \right)_{\mu}\left (p_1 + p_2 \right)^{\mu}$

The invariants $s_1$, $s_2$ and $s_3$ are not independent (the motivation for what is known as a Dalitz plot). Based on the definitions of these invariants and 4-momentum conversation one can show that

$s_1 + s_2 + s_3 = (P^2 -2Pp_1 +p_1^2) +(P^2 -2Pp_2 +p_2^2) + (P^2 -2Pp_3 +p_3^2)$

$=3P^2 -2P(p_1+p_2+p_3) +p_1^2+p_2^2+p_3^2$

$=3P^2 -2P^2 +p_1^2+p_2^2+p_3^2$

$=P^2 +p_1^2+p_2^2+p_3^2$

$=M^2 + m_1^2 + m_2^2 +m_3^2$

Also Note

$\sqrt{s_1}$ is the invariant mass of a subsystem defined by treating daughter particles 2 and 3 as one object. similar interpretations for $\sqrt{s_2}$ and $\sqrt{s_3}$.

There are limits to the values of the invariant masses $s_1$ - $s_3$

In the Center of Momentum system we have the

$s_1 = M^2 +m_1^2 - 2ME_1$

because

$E_1 = m_1^2 + p_1^2$ we expect $E_1 \ge m_1$

This lead to

$\left . s_1 \right |_{max} = M^2 +m_1^2 - 2M(m_1) = (M-m_1)^2$

TO find the minimum value of $s_1$ we evaluate $s_1$ in the rest frame of the $m_2$, $m_3$ subsystem.

$s_1 = \left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}= (E_2^{cm2-3} +E_3^{cm2-3})^2 \gt (m_2 + m_3)^2$ : In the CM frame $E = \sqrt{p^2 +m^2} = m$

so the limits of s_1 are

$(m_2 + m_3)^2 \le s_1 \le (M-m_1)^2$

Invariant mass Dalitz plot Limits

Analagously you can show the the Min - Max limits for the $s_1$, $s_2$, and $s_3$ invariant masses are given by.

$(m_3 + m_1)^2 \le s_2 \le (M-m_2)^2$

$(m_1 + m_2)^2 \le s_3 \le (M-m_3)^2$

set theory notation is often used to express the above limits as

$s_1 \in \left [ (m_2 + m_3)^2 , (M-m_1)^2 \right ]$

$s_2 \in \left [ (m_3 + m_1)^2 , (M-m_2)^2 \right ]$

$s_2 \in \left [ (m_1 + m_2)^2, (M-m_3)^2 \right ]$

Dalitz plot boundary curve equation

Suppose we wish to plot a curve which describes the depence of s_1 on s_2 (determine s_2 as a function of s_1). This is refered to as a Dalitz plot in which $s_2$ appears on the x-axis (abscissa) and $s_1$ appears on the y-axis (ordinate). Becuase of the "squares" in the invariant mass, we can have two values of $s_2$ for a given value of $s_1$.

since

$s_2 = \left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}$

We should look seek equations for $p_1$ and $p_3$ in terms of masses$(M,m_1,m_2,m_3)$ and invariants $(s,s_1)$.

In order to find such expressions lets consider the problem as viewed by a reference frame in which $\vec{p}_3$ = -$\vec{p}_2$. This reference frame is sometimes referred to as the Jackson Frame (JF).

In the JF frame

$\vec{P}^{JF} = \vec{p}_1^{JF}$ : because the other two particles cancel the total momentum of the system is carried by $m_1$.

$s_1 \equiv = \left (P -p_1 \right)_{\mu}\left (P -p_1 \right)^{\mu}$

$=\left [ (E,-\vec{P}) - (E_1,-\vec{p_1})\right ]\left [ (E,\vec{P}) - (E_1,\vec{p}_1)\right ]$

$=\left [ (E^{JF},-\vec{P}^{JF}) - (E_1^{JF},-\vec{p}_1^{JF})\right ]\left [ (E^{JF},\vec{P}^{JF}) - (E_1^{JF},\vec{p}_1^{JF})\right ]$

$= (E^{JF}-E_1^{JF})^2 : \vec{P}^{JF}=\vec{p}_1^{JF}$

=$\left( \sqrt{M^2+(P^{JF})^2} - \sqrt{m^2+(p_1^{JF})^2}\right)$ : Def of $E_{tot}$

=$\left( \sqrt{M^2+(p_1^{JF})^2} - \sqrt{m^2+(p_1^{JF})^2}\right)$

where

$E^{JF}$ = total energy of Mother particle before it decays

$E_1^{JF}$ = total energy of $m_1$ particle

solving for $p_1^{JF}$

$\left( p_1^{JF}\right )^2 = \frac{1}{4s_1} \left [ s_1 -(M-m_1)^2\right ]\left [ s_1 -(M+m_1)^2\right ]$

The function $\lambda$ is defined such that

$\lambda(A,B^2,C^2) = \left [ A -(B-C)^2\right ]\left [ A -(B+C)^2\right ]$ : notice the "squared" arguments

$=A^2 + B^2 + C^2 -2AB -2BC -2CA$

since this solution above is so common in relativistic kinematics

$\Rightarrow \left( p_1^{JF}\right )^2 = \frac{1}{4s_1}\lambda(s_1,M^2,m_1^2)$

Doing an analogous calculation for the other form os s_1

$s_1 =\left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}$

we will find

$p_2^{JF} = p_3^{JF} = \frac{1}{4s_1}\lambda(s_1,m^2,m_3^2)$

Lets substitute $p_1$ and $p_3$ into the definition for $s_2$ in the Jackson Frame.

$s_2 = \left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}$

$=\left (p_3^{JF} + p_1^{JF} \right)_{\mu}\left (p_3^{JF} + p_1^{JF} \right)^{\mu}$

$=\left [ (E_1^{JF},-\vec{p}_1^{JF}) + (E_3^{JF},-\vec{p}_3^{JF})\right]\left [ (E_1^{JF},\vec{p}_1^{JF}) + (E_3^{JF},\vec{p}_3^{JF})\right]$

$= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} - p_1^{JF} p_2^{JF} \cos(\theta_{13})\right )$

where

$\cos(\theta_{13})$ = angle between $\vec{p}_1^{JF}$ and $\vec{p}_3^{JF}$

$p_1^{JF}$ and $p_2^{JF}$ are given above we just need to figure out what $E_1^{JF}$ and $E_2^{JF}$ are

If we assume $s_1$ is fixed (you generate the Dalitz plot boundary by determining the two values of $s_2$ for a given value of $s_1$) then

$E_1^{JF} = \frac{1}{2\sqrt{s_1}} (M^2 - s_1 -m_1^2)$

$E_3^{JF} = \frac{1}{2\sqrt{s_1}} (s_1 + m_3^2 -m_2^2)$

The only remaining unkown is the angle $(\alpha)$ between math>\vec{p}_1^{JF}</math> and $\vec{p}_3^{JF}$ which we can treat as either $\pi$ or 0 to determine the min and max values of s_2 for a given value of 2_1.

$s_2= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} - p_1^{JF} p_2^{JF} \cos(\theta_{13})\right )$

$= m_1^2 +m_3^2 + 2\left ( E_1^{JF} E_3^{JF} \pm p_1^{JF} p_2^{JF} \right )$

$= m_1^2 +m_3^2 + 2\left ( \frac{1}{2\sqrt{s_1}} (M^2 - s_1 -m_1^2) \frac{1}{2\sqrt{s_1}} (s_1 + m_3^2 -m_2^2) \pm p_1^{JF} p_2^{JF} \right )$

Substituting for $p_1^{JF}$ and $p_2^{JF}$

$s_2=m_1^2 +m_3^2 + \frac{1}{s_1} \left ((M^2 - s_1 -m_1^2)(s_1 + m_3^2 -m_2^2) \pm \sqrt{\lambda(s_1,M^2,m_1^2) \lambda(s_1,m_2^2,m_3^2)}\right )$

The above equation for $s_2$ defines a boundary line of the Dalitz plot. The kinematics of the particles in constrained to the interior of this bounding.

Example:$D_s^+$ Meson decay

Consider the $D_s^+$ meson which decays $\sim$ 5\% of the time into three particles; $K^+K^-\pi^+$

$M =1969 MeV$ for a$D_s^+$ Meson

$m_1 = 494 MeV$ for a $K^+$

$m_2 = 140 MeV$ is a $\pi^+$

$m_3=494 MeV$ is a $K^-$

Dalitz Plot limits are:

X-axis$(s_2)$

Min = $(m_3 + m_1)^2 = (988 MeV)^2 \; \sim 1 GeV^2$

Max = $(M-m_2)^2 = (1829 MeV)^2 = 3.35 GeV^2$

Y-axis $(s_1)$

Min $(m_2+m_3)^2 \; \sim (634 MeV)^2 = 0.402 GeV^2$

Max= $(M-m_1)^2 = (1475 MeV)^2 = 2.2 GeV^2$

The image below is from experiment E698

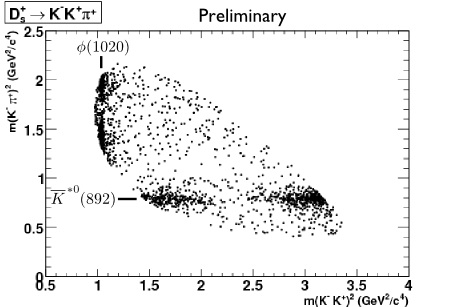
Notice the dark bands which have been labeled $\phi(1020)$ and $\bar{K}^{*0}(892)$. These dark bands indicate a tendency for the decay to clump into states with specific masses, namely $s_2=1.04 GeV^2 (\Rightarrow m=1020 MeV)$ and $s_1=0.796 GeV^2 (\Rightarrow m= 892 MeV^2)$. The isobar model suggests that the $D_s^+$ decays into two particles and then a third particle. In one case the decay is

$D_s^+ \rightarrow \phi^0 + \pi^+$

and then the $\phi$ decays via

$\phi^0 \rightarrow K^+ + K^-$

Notice that the dark bands are not infinitely thin but have widths as well. The uncertainty principle ($\Delta E \Delta t \gt \hbar$) suggest that only a particle with an infinite lifetime can have a finite , well defined, mass. The width of these dark bands can be used to determine the lifetimes of the intermediate $\phi$ and $\bar{K}^{*0}$ states.

Also notice that there are 2 "clumps" of darks spots in each dark band. The limits for $s_2$ where based on Min/Max values of the $\cos(\theta_{13})$ term. This term tells us how aligned or misaligned the momentum vecors of $m_1$ and $m_3$ (the Kaons)are.

Elastic Scattering

Given the elastic scattering of 2 particles such that the following properties are

Known

$m_1$ = mass of the incident particle #1

$m_2$ = mass of the target particle (at rest) #2

$p_1$ = momentum of the incident particle #1

$\theta_1$ = scattering angle of particle #1

You can show that

$p_1^{\prime} = \frac{-B \pm \sqrt{B^2 -4AC}}{2A}$ = Final momentum of scattered particle #1

$p_2^{\prime} = \left ( p_1^{\prime} \right )^2 -2p_1p_1^{\prime}\cos(\theta_1) + p_1^2$ = Final momentum of the target particle

$\sin (\theta_2) = - \frac{p_1^{\prime} \sin(\theta_1)}{p_2^{\prime}}$

where

$A = \left ( \sqrt{p_1^2 +m_1^2} +m_2 \right )^2 -p_1^2 \cos^2(\theta_1)$

$B = -2p_1 \cos(\theta_1) \left ( m_1^2 + m_2 \sqrt{p_1^2 + m_1^2}\right )$

$C = - \left [ m_1^4 + (m_2^2 -m_1^2)(p_1^2 + m_1^2) -m_1^2m_2^2\right ]$

In-Elastic Scattering

List of 4-vectors

$q^{\mu} \equiv ( \omega , \vec{q} )$ = momentum transfered from incident particle to target

$k_i^{\mu} \equiv (E_i, \vec{k}_i )$ = initial momentum of incident particle

$k_f^{\mu} \equiv (E_f, \vec{k}_f )$ = final momentum of incident particle

$q^{\mu} \equiv k_i^{\mu} - k_f^{\mu}$ = definition of momentum transfer based on conservation of momentum

Momentum Transfer Squared $(Q^2)$

The momentum transfer squared is given by

$q_{\mu}q^{\mu} = (E_i - E_f)^2 -(\vec{k}_i - \vec{k}_f ) (\vec{k}_i - \vec{k}_f )$

$=(E_i^2 -2E_iE_f +F_f^2) - ( |\vec{k}_i |^2 - 2 |\vec{k}_i| |\vec{k}_f| \cos(\theta) + | k_f |^2)$

$E^2 = | \vec{k} |^2 +m^2$

$\Rightarrow q_{\mu}q^{\mu} = \left ( | \vec{k}_i |^2 +m_i^2 - 2 E_i E_f +| \vec{k}_f |^2 +m_f^2\right ) - | \vec{k}_i |^2 - | \vec{k}_f |^2 + 2 | \vec{k}_i | | \vec{k}_f |^2 \cos(\theta)$

$= m_i^2 + m_f^2 - 2 E_i E_f + 2| \vec{k}_i | | \vec{k}_f |^2 \cos(\theta)$

In the case of electron scattering

$m_i = m_f$

$E_i \sim | \vec{k}_i |$

$E_f \sim | \vec{k}_f |$

$m \ll E$

$\Rightarrow q^2 = -2 | \vec{k}_i | | \vec{k}_f | \left ( 1 - \cos (\theta) \right )$

$= -4 | \vec{k}_i | | \vec{k}_f | \sin^2(\frac{\theta}{2}) \equiv -4 E_i E_f \sin^2(\frac{\theta}{2})$

if$q^2 \lt 0 \Rightarrow$ spacelike (scattering)

if $q^2 \gt 0 \Rightarrow$ timelike (free particle)

The Momentum Transfer squared for scattering is define as $Q^2$ such that

$Q^2 = -q^2$

Missing Mass $(W)$

Consider an inelastic scattering process where the particles have the 4-Momentum vectors defined as

$\left ( p_e^{\mu} \right ) \equiv (E_i, \vec{k}_i)$ = initial momentum 4-vector of the incident electron

$\left ( p_p^{\mu} \right ) \equiv (M_p, 0)$ = initial momentum 4-vector of the target proton

$\left ( p_e^{\mu} \right )^{\prime} \equiv (E_f, \vec{k}_f)$ = final momentum 4-vector of the scattered electron

$\left ( p_p^{\mu} \right )^{\prime} \equiv (E_X, \vec{p}_X)$ = final momentum 4-vector of the target proton

$W^2 \equiv \left (E_X^2 -p_X^2 \right )$ = mass of scattered proton

Conservation of 4-Momentum

$\left ( p_e \right )^{\mu} + \left ( p_p \right )^{\mu} = \left ( p_e^{\prime} \right )^{\mu} + \left ( p_p^{\prime} \right )^{\mu}$

solve for final proton momentum 4-vector and determine the length

$\left ( p_p^{\prime} \right )_{\mu} \left ( p_p^{\prime} \right )^{\mu} = \left [ \left ( p_e \right )^{\mu} + \left ( p_p \right )^{\mu} - \left ( p_e^{\prime} \right )^{\mu}\right ] \left [ \left ( p_e \right )_{\mu} + \left ( p_p \right )_{\mu} - \left ( p_e^{\prime} \right )_{\mu}\right ]$

$W^2 \equiv \left ( p_p^{\prime} \right )_{\mu} \left ( p_p^{\prime} \right )^{\mu}$

= $\left [ (E_i, \vec{k}_i) + (M_p, 0) - (E_f, \vec{k}_f) \right ]\left [ \left ( {E_i \atop \vec{k}_i }\right ) + \left ( {M_p \atop 0 }\right ) - \left ( {E_f \atop \vec{k}_f }\right )\right ]$

$= (E_i^2 - k_i^2 ) + (E_f^2 - k_f^2 ) + M_p^2 + 2 M_p(E_i - E_f) - 2(E_iE_f - \vec{k}_i \cdot \vec{k}_f )$

= $m_e^2 + m_e^2 +M_p^2 + 2 M_p(E_i - E_f) - 2(E_iE_f - \vec{k}_i \cdot \vec{k}_f )$

$q^2= m_i^2 + m_f^2 - 2 E_i E_f + 2| \vec{k}_i | | \vec{k}_f |^2 \cos(\theta)$

substitution

$W^2 = M_p^2 + 2M_p (E_i -E_f) + q^2 = M_p^2 + 2 M_p(E_i - E_f) -Q^2$

Tranform to Center of Mass

A relativistic transformation from a rest frame where $E,\vec{p}$ are given to a frame moving with velocity $\beta$ is given by

$\left ( \begin{matrix} E^{\prime} \\ p^{\prime}_x \\ p^{\prime}_y \\ p^{\prime}_z \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} E \\ p_x \\ p_y \\ p_z \end{matrix} \right )$

The velocity of the center of mass frame for the case of a fixed target scattering event (the target is at rest) is given by

$\vec v_{cm} c = \vec \beta = \frac{\vec{p_1}}{p^0} = \frac{\vec p_1}{E_1+m_2}$

where

$E_1,\vec p_1$ are the energy and momentum for the incident particle

$m_2$ is the mass of the target particle

$\beta = \frac{v}{c} = \frac{pc}{E}$

$\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2} = \frac{E_1 + m_2}{\sqrt{m_1^2+m_2^2+2 E_1m_2}}$

Assume an incident electron of 11 GeV moller scatters

$p_1^{\mu} = ( E_1, \vec p_1) = (sqrt{11^2+0.000511^2, 11 \hat i} )= (11.0000000118691,11 \hat i)$

$p_2^{\mu} = ( E_2,\vec 0) = (0.000511,0)$

$v_{cm} = \frac{m_1 v_1}{m_1+m_2}$

Using ROOT functions

TLorentzVector P1,P2;

set the momentum four vector for an 11 GeV electron

P1.SetPxPyPzE(11,0,0,sqrt(11*11+0.000511*0.000511))
P2.SetPxPyPzE(0,0,0,0.000511)

Check that you get the mass of the electron in Units of GeV

The invariant mass of the particle is given by

root [36] P1.Mag()
(const Double_t)5.11000016012715737e-04

The Beta and Gamma of the Particle are Given by

P1.Beta()
(const Double_t)9.99999998920987565e-01
root [42] P1.Gamma()
(const Double_t)2.15264184050203912e+04

The Kinetic Energy ($(\gamma-1)m_oc^2$) is Given by

root [43] (P1.Gamma()-1)*0.511
(const double)1.09994888049654201e+04
root [46] (P1.Gamma()-1)*P1.Mag()
(const double)1.09994891496458251e+01

assume you moller scatter off a free electron at rest.

Construct the boost vector

TLorentzVector CMS;

CMS=P1+P2;

P1.Boost(-CMS.BoostVector());
P2.Boost(-CMS.BoostVector());

root [138] P1.Px()
(const Double_t)5.30129176950140391e-02
root [139] P2.Px()
(const Double_t)(-5.30129176949399178e-02)

A final state moller scattering event from GEANT4 has

The scattered electron

P3.SetPxPyPzE(0.433025,-0.858867,10999.6,sqrt(0.433025*0.433025+0.858867*0.858867+10999.6*10999.6+ 0.000511*0.000511))

The moller electron

P4.SetPxPyPzE(-0.433025,0.858867,0.905366,sqrt(0.433025*0.433025+0.858867*0.858867+0.905366*0.905366+ 0.000511*0.000511))

CMS=P3+P4


P3.Boost(-CMS.BoostVector());
root [191] P4.Boost(-CMS.BoostVector());
root [192] P3.Px()
(const Double_t)4.33024999999999993e-01
root [193] P4.Px()
(const Double_t)(-4.33024999999999993e-01)
root [194] P3.Py()
(const Double_t)(-8.58867000000000047e-01)
root [195] P4.Py()
(const Double_t)8.58867000000000047e-01
root [196] P3.Pz()
(const Double_t)4.78021531980484724e+01
root [197] P4.Pz()
(const Double_t)(-4.78021531981362244e+01)
root [198] P3.E()
(const Double_t)4.78118292245973180e+01
root [199] P4.E()
(const Double_t)4.78118292247171723e+01

Back to Classes