Difference between revisions of "Alpha Ionization"

From New IAC Wiki
Jump to navigation Jump to search
 
(151 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
=Energy threshold for electron and gamma entering detector=
+
Alpha particles are highly ionizing and represent the main source for charge in QDC's charge spectrum. Alpha particles  are mostly emitted by heavy radioactive nuclei; alpha kinetic  energy is dependent on the mass difference before and after emission. For U-233,  85% of alpha particles has energy of 4.82 MeV when U-233 decays to an alpha particle and Th-229.<ref name ="Akovali"> Akovali, Y. (1990, January 1). Table of Radioactive Isotopes. Retrieved January 1, 2014. </ref>
  
−
Detemine the energy threshold that an electron and a photon need to surpass in order to pass through the kapton, gas, the copper cathode, and the FR4.
+
Performing the simulation for alpha charge  passed over specific stages started by using alpha's emission rates.  A simulation was benchmarked with published data to determine the amount of primary ionization produced from a single alpha particle for a given energy, the ionization that took  place when the primary electrons were accelerated in an external elective field, then the multiplication (gain) by the triple GEM  preamplifier structure. And finally, the simulation showed the impact of the shutter on alpha ionization when an FR4 shutter was in front of the U-233 coating.
  
−
Draw a picture with dimensions of all the layers
 
  
 +
=Alpha emission rates and their energies=
  
 +
Alpha particles has a continuous energy spectrum, which also give relative rates for the emitted alpha. The figure below shows the relative rates for each alpha,
  
−
Energy -vs- counts per incident particle
+
[[File: alpha_energy_percentages.png  | 300 px]]
 +
< ref name="Akovali"/>
  
 +
Alpha particles of an energy of 4.82 MeV has the highest rate of  85 percent compared to the other alpha energies' rates.
  
−
Photon and electron Energy -vs- distance through the detector
+
The number of alpha and beta particles were measured in the lab <ref> Roy Don</ref>. Before installing U-233 source to be a part of the detector cathode, the number of alpha and beta particles were measured using a standard calibrated drift chamber as shown in the table below,
  
−
 
+
   
−
 
+
{| border="1" celdetectorV"4"
−
energy straggling plot at the point where particle just makes it through the detector
 
−
 
 
−
=Alpha Particles ionization simulation using GEANT4=
 
−
 
 
−
GEANT4 simulates the ionization of alpha particles in Ar/CO2 90/10 gas. Geant4 can simulate the ionization process for alpha particles. Unfortunately the value of the step function  underestimates the number of delta electrons even after decreasing  the step cut to 1 nm. Also,using GEANT4 overestimates the range of alpha particles in Ar/CO2 gas when compared to those that srim calculates [[File:Alpha_range_ArCo2.txt]], the following table shows the maximum range of alpha particles that are emitted from the U-233, and the ranges calculated by srim.
 
−
 
 
−
{| border="1" cellpadding="5" cellspacing="0" align="center"
 
−
|-
 
−
| Alpha Energy (MeV)  || G4 Range (cm) || Srim Range (um)
 
−
|-
 
−
| 1.0 || 0.56599  || 129.49
 
−
|-
 
−
| 2.0 || 1.1467  || 255.91
 
 
|-
 
|-
−
| 3.0 || 1.9024  || 417.27
+
| Shutter position || Alpha particles /min.|| Beta particles /min.
 
|-
 
|-
−
| 4.0 || 2.8012  || 612.45
+
| Open || 6879 || 900
 
|-
 
|-
−
| 5.0 || 3.8425  || 839.91
+
| Close || 1 || 38
 
|}
 
|}
  
 +
The table shows that the shutter almost stopped all alpha and beta particles as it covered the source. Depending on alpha relative intensities, the source rate for emitting 4.82 MeV alpha (most probable) is  97 Hz.
  
−
[[File:AlphaEnergy_numberof_primary_electrons_Drift.png | 200px]]
+
=An alpha particle's primary and secondary ionization =
−
 
 
  
 +
The electric field determines the number of primary and secondary electrons in pure argon gas. When an alpha particle travels in pure argon, it liberates up to 30,000 electrons for primary and secondary ionization <ref> Fabio, S. (2014). Basic processes in gaseous counters. In Gaseous Radiation Detectors: Fundamentals and Applications. Cambridge: University Printing House </ref> without any electric field effect. On the other hand, Saito <ref name = "saito"> Saito, K., & Sasaki, S. (2003). Simultaneous Measurements of Absolute Numbers of Electrons and Scintillation Photons Produced by 5.49 MeV Alpha Particles in Rare Gases. IEEE TRANSACTIONS ON NUCLEAR SCIENCE, 50(6), 2452-2460 </ref> measured the number of primary and secondary electrons for a 5.49 MeV alpha particle when a 4.7 kV/cm drift electric field collected the free electrons in the drift area to a collector, the number of collected electrons reached to 200k electron. Saito's measurements shows that the collector almost counts for all electrons, so the electric field decreases the probability of any electron-ion reattachment.
  
 +
Simulations of GEANT4 <ref> Agostinelli, S. (2003). Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303 </ref> and Srim/Trim <ref>Ziegler, J. (2010). SRIM - The stopping and range of ions in matter (2010). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268(11-12), 1818-1823 </ref>  were used to estimate the number of primary and secondary electrons for an alpha particle, both of the tools are able to calculate the number of primary and secondary electrons  in a specific gaseous medium with  specific physical conditions for pressure, temperature, and density. The model in each tool was tested by estimating the range in Ar and  CO2 gases; the results are shown below:
  
 +
[[File:alpha_range_measured_simulated.png | 300px]]
 +
[[File:alpha_range_measured_simulated_CO2.png | 300px]]
  
−
Based on the previous table, GEANT4 failed to calculate the expected alpha range for most alpha energies, and underestimated the number of alpha's delta electrons emitted through that range, but it is still useful tool to simulate the primary delta electrons when negative beta particles pass through a defined medium.
+
According to the figures above, G4 succeeded to simulate the alpha range accurately in Ar and CO2 gases,  but the Srim/Trim model estimated the range with 50 percent less than that measured by Hanke and Bichsel  <ref> Hanke, C., & Bichsel, H. (1970). Precision energy loss measurements for natural alpha particles in argon. Kbh.: Det Kongelige Danske Videnskabernes Selskab </ref> in pure argon, while on the other hand, Srim/Trim estimated the same range of 4 cm for different alphas' energies in CO2.
  
−
=Alpha propagation through the drift area with 600V drift voltage=
+
G4 simulated the number of primary and secondary electrons in 1 cm of Ar/CO2 90/10 gas mixture, and the figures below show the results:
−
 
 
−
U-233 is an alpha-emitter source, alpha particles at least 4.85 MeV as kinetic energy when they leave the nucleus. The voltage needed to stop an alpha of an energy of 4.85 MeV can be calculated as the following:
 
−
 
 
−
 
 
−
<math> K.E_{alpha} = P.E_{drift}  = q \times  V</math> where V is the applied voltage.
 
−
 
 
−
for an alpha K.E = 4.85 MeV , q = 2e, so:
 
−
 
 
−
<math> 4.85 \times 10^6 \times e = 2e \times V </math>
 
−
 
 
−
<math> V = \frac{4.85 \times 10^6}{2} </math>
 
−
 
 
−
<math> V = 2.425 \times 10^6 V </math>
 
−
 
 
−
Compared to the  drift voltage, the drift voltage  effect is negligible, since the magnitude of work applied against each alpha is just 1.2 keV as shown below:
 
−
 
 
−
<math> W = q \times V </math>
 
−
 
 
−
<math> W = 2e * 1100 </math>
 
−
 
 
−
<math> W = 2.2 keV </math>
 
−
 
 
−
 
 
−
 
 
−
= Alpha's Ionization and Electron Rate Using G4=
 
−
 
 
−
 
 
−
Geant4 is used to estimate the number of electrons that are emitted in the drift region after in presence the FR4 shutter. Simulating alpha's ionization output in the drift region was divided in three stages:
 
−
 
 
−
# Alpha interaction with an FR4 shutter in vacuum.   
 
−
# Alpha interaction with an Ar/CO2 gas.   
 
−
# Alpha interaction with the FR4 shutter and the Ar/CO2 gas.
 
−
 
 
−
The first stage describes the alpha particles when they stopped by the FR4 shutter of thickness of 1 mm, the following figure shows the percentage of the number of alphas that penetrate the shutter, it shows for a complete penetration, alpha's energy has to be around 60 MeV. It is Previously mentioned that the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV, So the shutter is able to stop all the emitted alpha particles.
 
−
 
 
−
[[File:G4_alpha_tran_FR4_vacuum.png | 300px]]
 
−
 
 
−
 
 
−
As the shutter is open, the alpha particles travel through the drift region, a 1 cm deep of Ar/CO2 gas, primary electrons appear as a result of alpha collision with Ar-atoms which described in G4 as (hIoni) ionization. The number of primary electrons of each alpha particle is depend on its energy. the plot below shows the emitted alpha's primary electrons number in Ar/CO2 gas:
 
  
 
[[File:G4_1cmAr90CO2_alpha_primaryElecN.png | 300px]]
 
[[File:G4_1cmAr90CO2_alpha_primaryElecN.png | 300px]]
−
 
−
It is noticed that geant4 simulation for alpha's range in ArCO2 gas exceeds the depth of the drift region. So a decrease in the number of primary electrons as alpha's energy increases. GEANT4 alpha's range meets with STAR database on NIST website. (STAR calculated range is 7.4 cm for 8 MeV alpha particle passing through Ar-gas).
 
−
 
−
Looking at the number of secondary electrons, the figure shows that the number of secondary electrons that are collected in the drift region; the number of primary electrons is almost the same for all alpha's energies that are emitted from U-233. keeping in mind the plot for primary electrons; the number of secondaries increases  by increasing alpha's energy, i.e the kinetic energy of the primary electrons in case of 8.4 MeV alphas is more than those for 4.85 MeV alphas that made number of secondary electrons for all alpha's energy is almost the same. So the final rates for all alpha particles in the energy range of 4.85 MeV to 8.4 MeV is almost the same, since the number of secondary electrons is almost the same which is in average 300k electron/alpha assuming the same emission percentage for all alpha's energies.
 
−
 
 
[[File:G4_1cmAr90CO2_alpha_SecondElecN.png | 300px]]
 
[[File:G4_1cmAr90CO2_alpha_SecondElecN.png | 300px]]
  
  
−
[[File:G4_1cmAr90CO2_alpha_primElec_energy.png | 300px]] [[File:G4_1cmAr90CO2_alpha_SecondElec_energy.png | 300px]]
+
G4 estimated  2.7k secondary electrons when a 5.49 MeV alpha penetrated  1cm of the same medium without any applied electric field, the estimation is close to Saito's measurements, which could be interpreted that G4 did not consider the reattachment of the electrons as they were collected in the drift area to end up counting for all the free electrons in the gas. On the other hand,  the Scrim and Trim simulation for alpha particles ionizing 1cm of pure Ar gas estimated about  1 MeV deposited energy in the medium within that distance; it made the final number of electrons  around 37.5k electron (considering w = 26.7 eV/ip), which is the same estimation mentioned by Sauli.
  
 +
=Triple GEM gain=
  
 +
Garfield, well-known in simulating the interactions in gaseous media such as electron multiplication <ref> Garfield++. (n.d.). Retrieved June 1, 2013. </ref>, simulated the electron multiplication in Ar/CO2 gas in GEM detector. Garfield simulated the physical processes that occurred in triple GEM based detector by using more than one software package simultaneously. Furthermore, Garfield uses HEED and Magboltz that simulate electron interactions in different gases, and give the solution for the Boltzmann equation in 3D. It also uses a finite element method (FEM) package to map the electric field within specific boundary conditions of GEM preamplifiers.
  
 +
Garfield simulated a triple GEM detector electron multiplication in more than one region in the detector. When the electric field of 1-4kV/cm drives the electrons toward the first GEM preamplifier in 1cm drift region, electrons interact with the gas atoms and molecules. According to Garfield simulation for the drift region, A 200eV electron multiplies to 8 +_1 electrons before it reaches the first GEM preamplifier. In addition, Garfield simulated the gain for a triple GEM stack for Ar/CO2 93/7 as in  figure XX. The figure shows that Garfield estimated almost the same measured gain for triple GEM when voltage difference for each GEM preamplifier is 300V and 320V; however, as the voltage increased to 340V, Garfield overestimated the gain up to 25% more than the measured value.
  
−
Geant4 doesn't use direct ionization cross section database reference to simulate the ionization process, but geant4 considers the ionization as a combination of number of physical processes as mentioned in the link. [http://geant4.cern.ch/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/node63.html]
 
  
−
=Calculating the number of the delta electrons without using GEANT4=
+
[[File:ref_data_gain_triple_Ar93_CO2.png| 300px ]]
  
−
There is another way to calculate the number of delta electrons without using GEANT4. It starts by calculating the average energy loss <math> \Delta E_a</math> by the alpha particles and the average energy loss per unit length <math> {\zeta} </math> in Ar/CO2 gas using the Bethe-Block equation. It then uses the the following equation:
+
=FR4 Shutter Effect=
  
−
<math > \lambda = \frac{ \Delta E - \Delta E_a}{\zeta} </math>
+
Simulations and measurements proved that an FR4 plate almost stops all Alpha particles that are emitted from U-233. An FR4 plate of 1 mm thickness has been used as a shutter to stop alpha and beta particles. Roy's (2012) and different QDC's measurements have shown a difference in the number of counts  when the shutter is open, and when it was close covering the whole U-233 coating. The difference proved the shutter ability to stop alpha particles. Also GEANT4 simulated 1 mm FR4 ability to stop alpha particles, and predicted the alpha particle energy that would be able to penetrate the shutter as shown in the figure yy, For a complete penetration, alpha's energy has to be around 55 MeV, as previously stated. the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV and most probable energy of 4.82 MeV, The result indicates  that the shutter is able to stop all the emitted alpha particles in the drift region with a minimum ionization shown in QDC spectrum.
  
−
to calculate the actual energy loss by ionization  <math> \Delta E </math>,
 
−
where  <math > \lambda </math> represents random landau number.
 
  
−
By dividing the energy loss by the minimum energy for producing a pair of ion/electron pair W, this equation yields the number of electrons emitted by ionization.
+
[[File:G4_alpha_tran_FR4_vacuum.png | 300px]]
−
 
 
−
Srim can simulate the motion of an alpha particle in Ar/CO2 gas by allowing for the change in the stopping power per unit length. It can also show the ionization energy loss as shown in the following figure:
 
−
 
 
−
[[File:4.8MeV_ionization_ArCo2.jpeg | 200px]]
 
−
 
 
−
This figure shows the ionization energy loss of 1000 alpha particles as they pass through Ar/CO2 gas of length of 1 cm.
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
 
 
−
{| border="1" cellpadding="5" cellspacing="0" align="center"
 
−
|-
 
−
|-Bethe block formula calculates the average ionization energy loss as the following:
 
−
|-<math>- \frac{dE}{dx} = \frac{4 \pi}{m_e c^2} \cdot \frac{nz^2}{\beta^2} \cdot \left(\frac{e^2}{4\pi\varepsilon_0}\right)^2 \cdot \left[\ln |-\left(\frac{2m_e c^2 \beta^2}{I \cdot (1-\beta^2)}\right) - \beta^2\right]</math>
 
−
 
 
−
|-for an electron of rest mass <math> m_ec^2 = 0.511 MeV </math>,
 
−
|-and <math> m_{\alpha}c^2 = 3.727 MeV </math>
 
−
|}
 
−
 
 
−
=Number of Primary  ionization events per cm=
 
−
 
 
−
;Inside the chamber
 
−
 
 
−
[[File:PhotonEnergy_numberof_primary_electrons_Drift.png | 200px]]
 
−
[[File:PhotonEnergy_numberofphotonsabsorbedwithin1cm.png | 200px]]
 
−
 
 
−
The figures show the threshold energy for photons traveling in the detector and the number of the absorbed photons within the detector's drift area. Photons travel through the drift area and primarily interact by photoelectric effect with the gas's atoms and molecules; a photon's energy may increase up to 1.1 MeV and still the most probable interaction with the medium is the photoelectric effect. Figure xx1 shows the same numbers of primary electrons produced by an incident photon simulation by GEANT4; once when all photon's interactions are considered (red), and once when only the photoelectric effect only considered (blue). It also shows that all the photons are absorbed by Ar/CO2 gaseous medium. Since the incident photon energy varies from 10 keV up to 1.1 MeV, only the absorbed photons within a 1 cm will affect the detector signal. GEANT4 simulation shows that the dominant interaction is the photoelectric effect even if the incident photon energy reaches 1.1 MeV, and that 25 percent of the photons will be absorbed when their energy is 25 keV, as the energy increases the number of photons decreases to reach 0.03 when the photon energy is 96.1 keV. As a result, gamma energy, emitted by U-233 or bremsstrahlung radiation that appears when the lineac is in operation, should have a maximum energy of 96.1 keV as it is in the detector's drift area, which maximizes the effect on the detector's signal.
 
−
 
 
−
;7cm Outside the chamber
 
−
 
 
−
Photons may reach the detector's drift area and affect its signal when they pass through the kapton window or (less probably) through the ertalyte plastic. Normally, the detector structure is built from materials that prevent the photons of specific energies from causing ionization in the drift area. Figure xx3 shows the incident photon energy at a 7 cm distance from the kapton window and the number of photons absorbed in the drift area that cause ionization by photoelectric effect.
 
−
 
−
 
 
−
[[File:PhotonEnergy_numberofphotonsabsorbedwithin7cm_out.png | 200px]]
 
−
 
 
−
The figure shows a maximum number of absorbed photons; when the incident photon energy is 60 keV, 46 percent of the photons get absorbed by the drift region.
 
−
 
 
−
==from beta particle as a function of beta particle energy  using Garfield and GEANT4==
 
−
 
 
−
GEANT4 can simulate the primary number of delta electrons for a negative beta particle penetrating ArCO2. Using the TestEm10 example and choosing the appropriate default cut, GEANT4 counts the same number of primary delta electrons for negative beta particles with 1.1 MeV energy, and determines the energy and the momentum of the delta electrons depending on Moller or Bhabha's scattering, and depending on the value of the kinetic energy cut used.<ref name = "Urban">Urbán, L. (1998, 10 09). Geant4 physics reference manual. Retrieved from http: //geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/node41.html </ref>
 
−
 
 
−
The following figure shows Garfield simulation for the number of electrons that are collected in the drift region when the shutter is open and as the electron passes a 90/10 Ar/CO2 gas:
 
−
 
 
−
 
 
−
[[File:neg_beta_vs_numberof_primary_electrons_Garf.png | 200px]]
 
−
[[File:G4_electron_primaryeN.png | 200px]]
 
−
[[File:garf_G4_Pelec_ion.png | 200px]]
 
−
 
 
−
Overlay with dE/dx formula and fill in gaps
 
−
 
 
−
something is wrong with G4 result for electron energies below 1 keV.
 
−
 
 
−
==from photon as a function of photon particle energy  using Garfield and GEANT4==
 
−
 
 
−
[[File:photon_eprimary.png | 200px]]
 
−
 
 
−
[[File:photoionization_Ar.png | 200px]]
 
−
 
 
−
 
 
−
== Chamber Geometry in GEANT4==
 
−
 
 
−
The chamber geometry for the GEM chamber is set for Calculating the created charge in the detector's drift area is shown below:
 
−
 
 
−
[[File:G4_chamber_design.png | 200px]]
 
−
 
 
−
== Charge particles and photons primary ionization==
 
−
 
 
−
The physical interactions that take place inside the detector are simulated by GEANT4.9.6 to estimate the primary charge collected by the drift electric field in GEM detector. GEM detector depends mainly on the particles’ interaction with Ar/CO2 atoms and molecules, especially those that directly (or indirectly) produce free charge that can be collected by the drift electric field. Specifically in the GEM detector described by section XX, the detector signal can be produced by gamma rays, electrons, or neutrons. GEANT4.9.6 has been used to estimate the primary charge caused by those particles in case of electrons and neutrons, but for photons, GENAT4 is used to produce the photoionization energy spectrum for Ar/CO2 gas.
 
−
 
 
−
 
 
−
The simulation started by determining the number of primary electrons produced by charged particles in Ar/CO2. The number of primary electrons depends on the particles’ charge and mass and kinetic energy. As a result, alpha particles have the highest number of primary electrons,  electrons have less primary electrons, and photons have the least number of primary electrons  produced  per photon, assuming that photoabsorption is the dominant process in Ar/CO2 gas for an energy range of 1 to 300eV.
 
−
 
 
−
By modifying EmTest10 example in GEANT4.9.6, the number of primary electrons produced by an electron travels 1 cm is shown in the figure below:
 
−
 
 
−
[[File:garf_G4_Pelec_ion.png | 200px]]
 
−
 
 
−
The figure also shows Garfield simulation for an electron's primary ionization; it is noticed that the GEANT4.9.6 results match those of Garfield when the minimum incident electron energy is  <math> 2x10^4</math>eV. Such an energy value is much lower than the threshold kinetic energy which an electron needs to make ionizations in the detector's drift region, since the threshold kinetic energy for an electron is more than 2 MeV 5cm away from the detector's window.
 
−
 
 
−
GEANT4.9.6 predicts the number of the primary electrons for a photon. Photon ionization has the least number of electrons, even producing an free electron is constrained to the electronic structure of Ar/CO2 gas.
 
−
 
 
−
[[File:photon_eprimary.png | 200px]]
 
−
[[File:photoionization_Ar.png | 200px]]
 
−
 
 
−
GENAT4.9.6 does not predict the Argon photoabsorption spectrum specifically for each energy as shown above, the photon energy may have  <math> \pm 1</math>eV shift. It is worth to mention if the photon is not in the drift region, then the detector is completely blind for any photon of energy of 20-300 eV (their range in fm). In case of a 50 keV photon or more, the photon will easily pass the detector chamber without affecting its medium if only photoionization is considered, within that energy range Compton scattering cross section increases, it will produce an electron and a photon in the drift region that can easily be detected. Being in am accelerator environment, photon interaction becomes dominant by Compton Scattering interaction in a way that makes the detector in efficient to detect any other particle.
 
−
 
 
−
=Total charge on anode=
 
−
 
 
−
Now use the primary above and include detector gain to calculate total charge hitting the anode and getting readout.
 
  
  
 +
[[alpha particle simulation related]]
  
 
<References/>
 
<References/>
−
 
−
 
−
 
−
 
−
 
−
 
  
  
 
GO BACK [https://wiki.iac.isu.edu/index.php/Performance_of_THGEM_as_a_Neutron_Detector#Alpha.2C_electrons.2C_photons_ionization]
 
GO BACK [https://wiki.iac.isu.edu/index.php/Performance_of_THGEM_as_a_Neutron_Detector#Alpha.2C_electrons.2C_photons_ionization]

Latest revision as of 15:25, 8 April 2015

Alpha particles are highly ionizing and represent the main source for charge in QDC's charge spectrum. Alpha particles are mostly emitted by heavy radioactive nuclei; alpha kinetic energy is dependent on the mass difference before and after emission. For U-233, 85% of alpha particles has energy of 4.82 MeV when U-233 decays to an alpha particle and Th-229.<ref name ="Akovali"> Akovali, Y. (1990, January 1). Table of Radioactive Isotopes. Retrieved January 1, 2014. </ref>

Performing the simulation for alpha charge passed over specific stages started by using alpha's emission rates. A simulation was benchmarked with published data to determine the amount of primary ionization produced from a single alpha particle for a given energy, the ionization that took place when the primary electrons were accelerated in an external elective field, then the multiplication (gain) by the triple GEM preamplifier structure. And finally, the simulation showed the impact of the shutter on alpha ionization when an FR4 shutter was in front of the U-233 coating.


Alpha emission rates and their energies

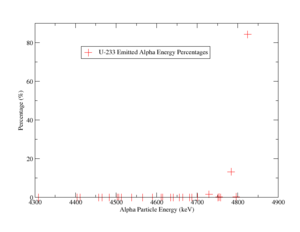
Alpha particles has a continuous energy spectrum, which also give relative rates for the emitted alpha. The figure below shows the relative rates for each alpha,

Alpha energy percentages.png < ref name="Akovali"/>

Alpha particles of an energy of 4.82 MeV has the highest rate of 85 percent compared to the other alpha energies' rates.

The number of alpha and beta particles were measured in the lab <ref> Roy Don</ref>. Before installing U-233 source to be a part of the detector cathode, the number of alpha and beta particles were measured using a standard calibrated drift chamber as shown in the table below,


Shutter position Alpha particles /min. Beta particles /min.
Open 6879 900
Close 1 38

The table shows that the shutter almost stopped all alpha and beta particles as it covered the source. Depending on alpha relative intensities, the source rate for emitting 4.82 MeV alpha (most probable) is 97 Hz.

An alpha particle's primary and secondary ionization

The electric field determines the number of primary and secondary electrons in pure argon gas. When an alpha particle travels in pure argon, it liberates up to 30,000 electrons for primary and secondary ionization <ref> Fabio, S. (2014). Basic processes in gaseous counters. In Gaseous Radiation Detectors: Fundamentals and Applications. Cambridge: University Printing House </ref> without any electric field effect. On the other hand, Saito <ref name = "saito"> Saito, K., & Sasaki, S. (2003). Simultaneous Measurements of Absolute Numbers of Electrons and Scintillation Photons Produced by 5.49 MeV Alpha Particles in Rare Gases. IEEE TRANSACTIONS ON NUCLEAR SCIENCE, 50(6), 2452-2460 </ref> measured the number of primary and secondary electrons for a 5.49 MeV alpha particle when a 4.7 kV/cm drift electric field collected the free electrons in the drift area to a collector, the number of collected electrons reached to 200k electron. Saito's measurements shows that the collector almost counts for all electrons, so the electric field decreases the probability of any electron-ion reattachment.

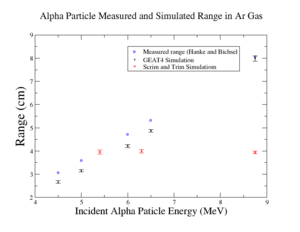
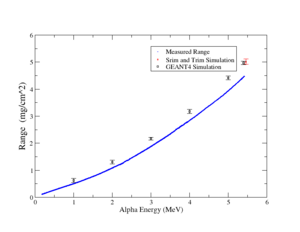
Simulations of GEANT4 <ref> Agostinelli, S. (2003). Geant4—a simulation toolkit. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303 </ref> and Srim/Trim <ref>Ziegler, J. (2010). SRIM - The stopping and range of ions in matter (2010). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 268(11-12), 1818-1823 </ref> were used to estimate the number of primary and secondary electrons for an alpha particle, both of the tools are able to calculate the number of primary and secondary electrons in a specific gaseous medium with specific physical conditions for pressure, temperature, and density. The model in each tool was tested by estimating the range in Ar and CO2 gases; the results are shown below:

Alpha range measured simulated.png Alpha range measured simulated CO2.png

According to the figures above, G4 succeeded to simulate the alpha range accurately in Ar and CO2 gases, but the Srim/Trim model estimated the range with 50 percent less than that measured by Hanke and Bichsel <ref> Hanke, C., & Bichsel, H. (1970). Precision energy loss measurements for natural alpha particles in argon. Kbh.: Det Kongelige Danske Videnskabernes Selskab </ref> in pure argon, while on the other hand, Srim/Trim estimated the same range of 4 cm for different alphas' energies in CO2.

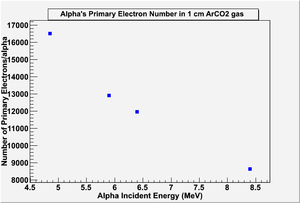
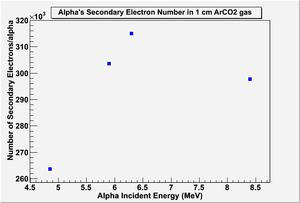
G4 simulated the number of primary and secondary electrons in 1 cm of Ar/CO2 90/10 gas mixture, and the figures below show the results:

G4 1cmAr90CO2 alpha primaryElecN.png G4 1cmAr90CO2 alpha SecondElecN.png


G4 estimated 2.7k secondary electrons when a 5.49 MeV alpha penetrated 1cm of the same medium without any applied electric field, the estimation is close to Saito's measurements, which could be interpreted that G4 did not consider the reattachment of the electrons as they were collected in the drift area to end up counting for all the free electrons in the gas. On the other hand, the Scrim and Trim simulation for alpha particles ionizing 1cm of pure Ar gas estimated about 1 MeV deposited energy in the medium within that distance; it made the final number of electrons around 37.5k electron (considering w = 26.7 eV/ip), which is the same estimation mentioned by Sauli.

Triple GEM gain

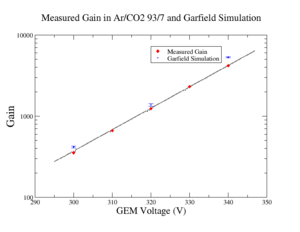
Garfield, well-known in simulating the interactions in gaseous media such as electron multiplication <ref> Garfield++. (n.d.). Retrieved June 1, 2013. </ref>, simulated the electron multiplication in Ar/CO2 gas in GEM detector. Garfield simulated the physical processes that occurred in triple GEM based detector by using more than one software package simultaneously. Furthermore, Garfield uses HEED and Magboltz that simulate electron interactions in different gases, and give the solution for the Boltzmann equation in 3D. It also uses a finite element method (FEM) package to map the electric field within specific boundary conditions of GEM preamplifiers.

Garfield simulated a triple GEM detector electron multiplication in more than one region in the detector. When the electric field of 1-4kV/cm drives the electrons toward the first GEM preamplifier in 1cm drift region, electrons interact with the gas atoms and molecules. According to Garfield simulation for the drift region, A 200eV electron multiplies to 8 +_1 electrons before it reaches the first GEM preamplifier. In addition, Garfield simulated the gain for a triple GEM stack for Ar/CO2 93/7 as in figure XX. The figure shows that Garfield estimated almost the same measured gain for triple GEM when voltage difference for each GEM preamplifier is 300V and 320V; however, as the voltage increased to 340V, Garfield overestimated the gain up to 25% more than the measured value.


Ref data gain triple Ar93 CO2.png

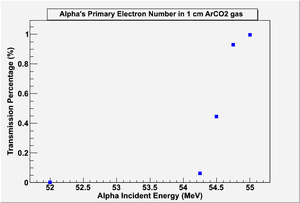
FR4 Shutter Effect

Simulations and measurements proved that an FR4 plate almost stops all Alpha particles that are emitted from U-233. An FR4 plate of 1 mm thickness has been used as a shutter to stop alpha and beta particles. Roy's (2012) and different QDC's measurements have shown a difference in the number of counts when the shutter is open, and when it was close covering the whole U-233 coating. The difference proved the shutter ability to stop alpha particles. Also GEANT4 simulated 1 mm FR4 ability to stop alpha particles, and predicted the alpha particle energy that would be able to penetrate the shutter as shown in the figure yy, For a complete penetration, alpha's energy has to be around 55 MeV, as previously stated. the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV and most probable energy of 4.82 MeV, The result indicates that the shutter is able to stop all the emitted alpha particles in the drift region with a minimum ionization shown in QDC spectrum.


G4 alpha tran FR4 vacuum.png


alpha particle simulation related

<References/>


GO BACK [1]

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Alpha_Ionization&oldid=100217"