VanWasshenova Thesis
Introduction
Moller Scattering
Moller Scattering Definition
Variables_Used_in_Elastic_Scattering
DV_Calculations_of_4-momentum_components
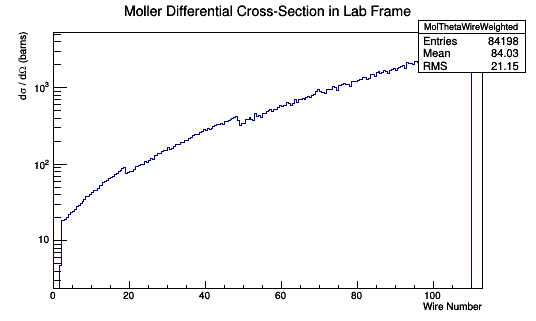
Moller Differential Cross-Section
GEANT4 Simulation of Moller Scattering
LH2 Target
Simulation Setup
NH2 Target
LH2 Vs. NH3
Effects Due to Target Material
Target Density
Atomic Mass and Electron Number Effects
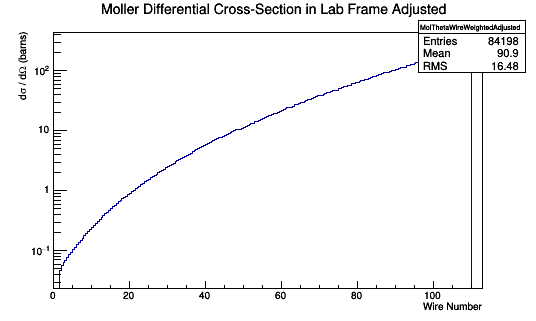
Differential Cross-Section Offset
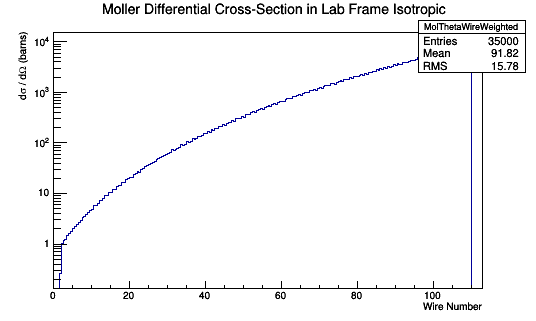
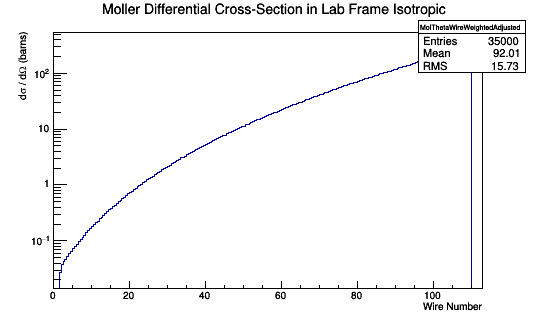
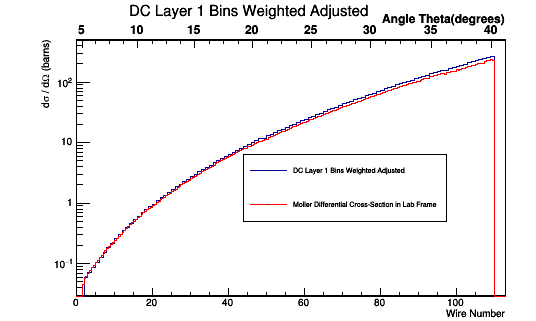
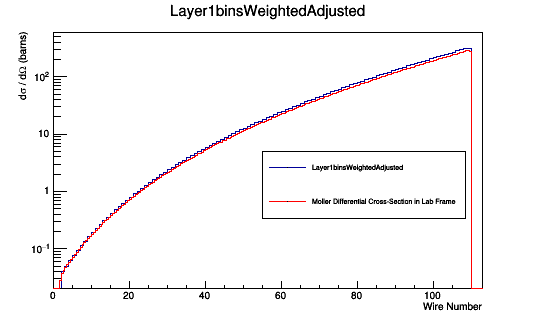
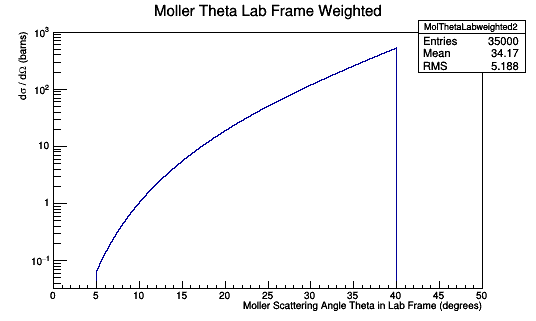
Weighted Isotropic Distribution in Lab Frame
GEMC Simulation
Drift Chamber
Determining wire-theta correspondence
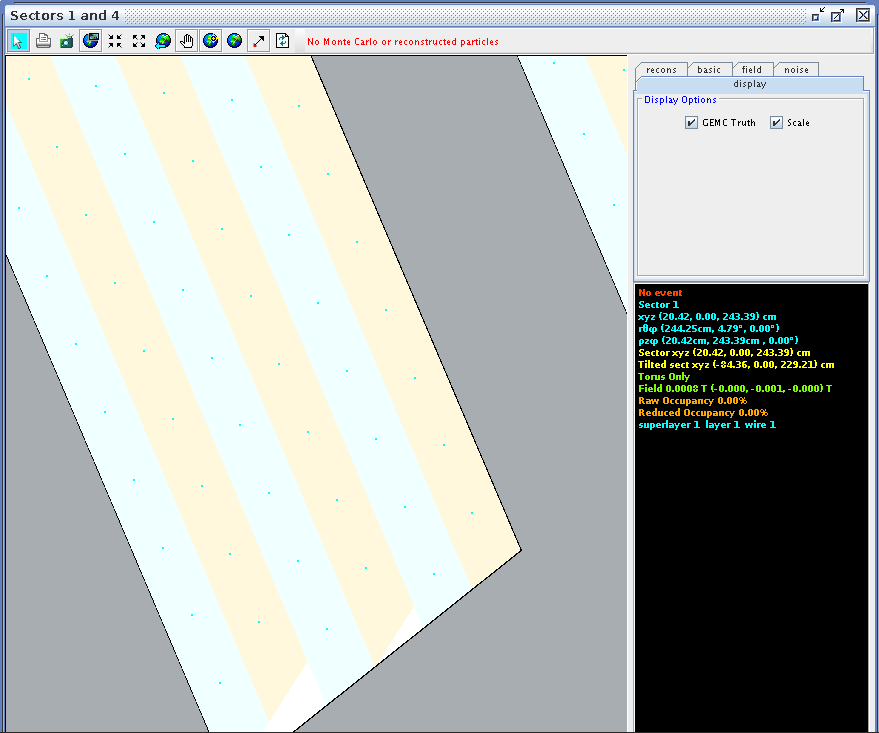
CED Verification
Using CED to verify the angle and wire correlation,
Zooming in on the view paralell to the direction of the wires in ced, we can examine the wire corresponding theta angle in the drift chamber.
| Coordinates(cm) | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| x | 20.42 | 21.51 | 21.39 | 22.49 | 22.37 | 23.47 |
| y | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| z | 243.41 | 244.18 | 245.51 | 246.28 | 247.62 | 248.38 |
| Coordinates(cm) | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| x | 21.64 | 22.73 | 22.61 | 23.71 | 23.58 | 24.69 |
| y | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| z | 242.86 | 243.62 | 244.94 | 245.71 | 247.05 | 247.81 |
Corresponding theta angles can be found for other wires, in Region 1, Superlayers 1 and 2.
| Wire Number | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| 1 | 4.79 | 5.03 | 4.98 | 5.22 | 5.16 | 5.40 |
| 2 | 5.09 | 5.33 | 5.27 | 5.51 | 5.45 | 5.69 |
| 62 | 24.42 | |||||
| 63 | 24.76 | |||||
| 64 | 25.10 | |||||
| 77 | 29.46 | 29.60 | 29.41 | 29.55 | 29.37 | 29.51 |
| 78 | 29.79 | 29.93 | 29.74 | 29.88 | 29.69 | 29.83 |
| 79 | 30.12 | 30.26 | 30.07 | 30.21 | 30.02 | 30.16 |
| 110 | 40.19 | 40.28 | 40.05 | 40.13 | 39.91 | 39.99 |
| 111 | 40.51 | 40.59 | 40.36 | 40.44 | 40.21 | 40.29 |
| 112 | 40.82 | 40.90 | 40.67 | 40.75 | 40.52 | 40.60 |
| Wire Number | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| 1 | 4.79 | 5.03 | 4.98 | 5.22 | 5.16 | 5.40 |
| 2 | 5.09 | 5.33 | 5.27 | 5.51 | 5.45 | 5.69 |
| 77 | 29.46 | 29.60 | 29.41 | 29.56 | 29.37 | 29.51 |
| 78 | 29.79 | 29.93 | 29.74 | 29.88 | 29.70 | 29.84 |
| 79 | 30.13 | 30.27 | 30.07 | 30.21 | 30.02 | 30.16 |
| 110x | 40.19 | 40.28 | 40.05 | 40.13 | 39.91 | 39.99 |
| 111 | 40.51 | 40.59 | 40.36 | 40.44 | 40.22 | 40.30 |
| 112 | 40.82 | 40.90 | 40.67 | 40.75 | 40.52 | 40.60 |
Super Layer 1:Layer 1
| Coordinates(cm) | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 |
|---|---|---|---|---|---|---|
| 1.22 | 1.22 | 1.22 | 1.22 | 1.21 | 1.22 | |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| .55 | .56 | .57 | .57 | .57 | .57 |
Using the geometric construction for determining angle theta to wire 2:
This equation can be solved for a hypothetical wire 0, which will allow the wire number to be the multiplicative factor for the change from the starting position.
where
Using Mathematica, a series expansion about n=0 can be found:
In[1]:= Series[ArcTan[(19.21+1.212 x)/(243.39-0.5652 n)],{n,0,4}]
Out[1]= 0.0787635+0.00513098 n+9.83726*10^-6 n^2-2.61675*10^-8 n^3-2.22826*10^-10 n^4+O[n]^5
This expression will find the angle theta in radians given the wire number. To convert from radians to degrees, we can multiply by 180 and divide by Pi.
In[2]:= 180*(0.07876354504106763`+0.005130982891104289` n+9.837257652182922`*^-6 n^2-2.616751708660921`*^-8 n^3-2.2282595631625944`*^-10 n^4+O[n]^5)/3.14159625359 Out[2]= 4.51281+0.293983 n+0.000563633 n^2-1.49929*10^-6 n^3-1.2767*10^-8 n^4+O[n]^5
This tells us that the expression for theta will follow a function that comes from a series expansion. To account for instrument and measurement errors, angle measurements from ced can be used to find a better fit.
Using Mathematica, a line can be fitted to the data collected on the wire number to angle theta correspondence.
Declaring the data set:
In[1]:= data1={{1,4.79},{2,5.09},{62,24.42},{63,24.76},{64,25.10},{78,29.79},{111,40.50},{112,40.82}}
Out[1]= {{1,4.79},{2,5.09},{62,24.42},{63,24.76},{64,25.1},{78,29.79},{111,40.5},{112,40.82}}
Testing for a linear fit:
In[2]:= line1=Fit[data1,{1,n},n]
Out[2]= 4.39975 + 0.32469 n
Examing the range limits for the angle theta for layer 1:
Taking the difference of the upper and lower limits in theta,
Dividing by the change in wire numbers (112-1=111), we find
This would imply that if the wires were evenly placed, their change in angle theta would increase by the factor of .325 degrees for each increase in wire number, starting obviously with wire 1 at 4.79 degrees. In addition, this implies that the bin spacing for each wire would be around .325 degrees in width.
Chercking this, we can find the difference between wires 1 and 2,
Similarly, finding the difference between wires 111 and 112,
These differing values show that the bin width is not uniform in length, therefore a first order, linear fit, will not suffice.
Testing for a quadratic fit:
In[3]:= quad1=Fit[data1,{1,n,n^2},n]
Out[3]= 4.45564 +0.32015 n+0.0000417787 n^2
The quadratic fit does not work since it's first derivative
does not give the same spacing between low and high values of n as seen in the ced data. The coefficient near the first order will have to smaller than .31 to find a correlation that would agree.
Testing for a polynomial of degree 3 fit:
In[4]:= polynomial1=Fit[data1,{1,n,n^2,n^3},n]
Out[4]= 4.49876 +0.293001 n+0.000679074 n^2-3.57132*10^-6 n^3
This fit best matches the data found in ced
As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number.
The derivative of this function then will tell us where the bin spacing is at a minimum and a maximum.
Comparing this maximum, we can see from Table 3 that near the maximum of 63 are seperated by larger distances than at n=1 or n=112. This is the midpoint of the plane as seen in the geometry file.
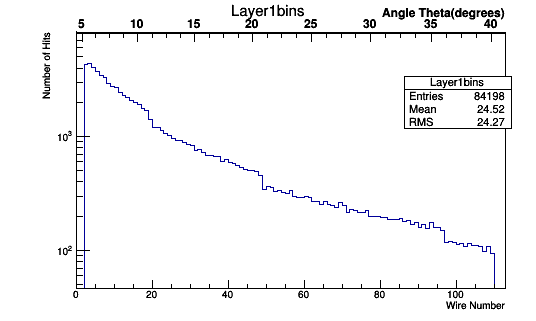
Binning based on wire numbers
The bin size based on wire number will need to be a uniform width of 1, as in an increment of 1 between the integer values of the wires. This uniformity in bin size based on wire numbers is not uniform when viewed by the angle theta due to the Drift Chamber geometry discussed earlier.
Modifying evioreader
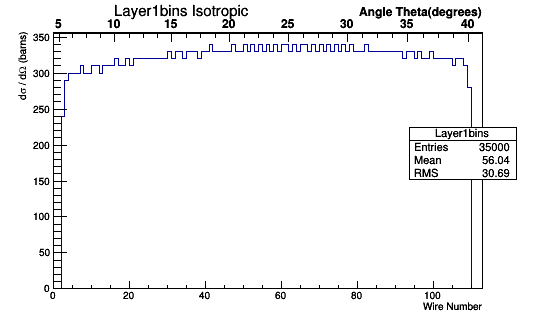
gStyle->SetStripDecimals(kTRUE);
TF1 *fit_function=new TF1("fit_function","[0]+[1]*x+[2]*x*x+[3]*x*x*x",4.49876,41.12592);
fit_function->SetParameters(4.49876,0.293001,0.000679074,-0.00000357132);
TGaxis *A1 = new TGaxis(0,5000,113,5000,"fit_function",510,"-");
A1->SetTitle("Angle Theta(degrees)");
A1->Draw();
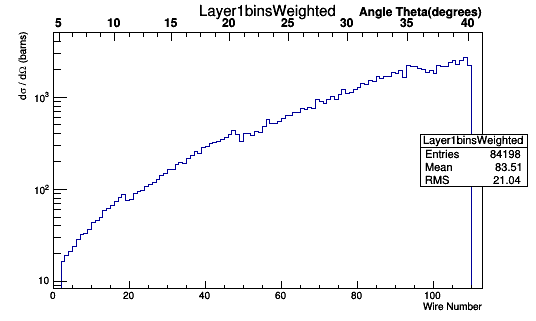
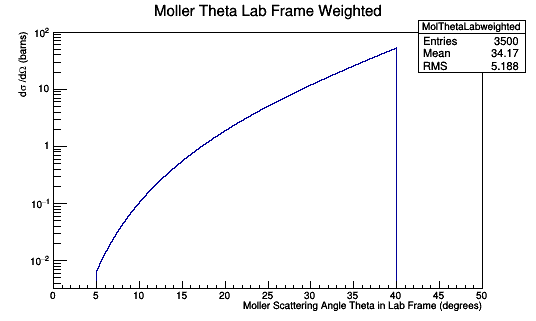
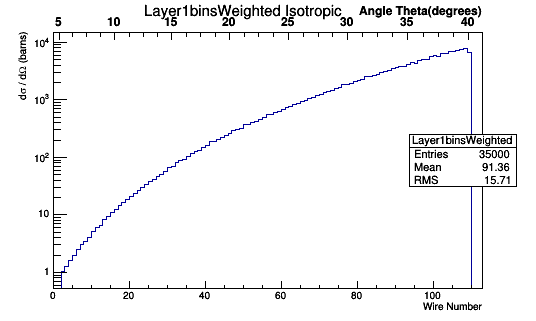
Using the expression for n in terms of Theta:
This relationship can be used to multiply each Moller Scattering angle theta in the lab frame, with it's differential cross-section weight, to find the Moller differential cross-section as a function of wire number in the lab frame.