Theory

Theoretical Descriptions of the Nucleon

The Standard Model

The Standard Model of particle physics, a Quantum Field Theory, was developed between 1970 and 1973. The Standard Model describes all of the known elementary particles interactions except gravity. It is the collection of the following related theories quantum electrodynamics, the Glashow-Weinberg-Salam theory of electroweak processes and quantum chromodynamics.
As it is known the matter is made out of three types of elementary particles: quarks, leptons and mediators.In the Standard Model there are six quarks,including the up(u) and down(d) quarks, which make up the neutron and proton. They are classified according to charge(Q), strangeness(S), charm(C), beauty(B) and truth(T). All quarks are spin- 1/2 fermions(1)

THE QUARK CLASSIFICATION

Generation	q	Q	D	U	S	C	B	T
Generation 1	d(down)	-1/3	-1	0	0	0	0	0
Generation 1	u(up)	2/3	0	1	0	0	0	0
Generation 2	s(strange)	-1/3	0	0	-1	0	0	0
Generation 2	c(charm)	2/3	0	0	0	1	0	0
Generation 3	b(bottom)	-1/3	0	0	0	0	-1	0
Generation 3	t(top)	2/3	0	0	0	0	0	1

There are six leptons electron, muon and tau, with their partner neutrino. Leptons are classified by their charge(Q), electron number([math]L_e[/math]), muon number([math]L_\mu[/math]) and tau number([math]L_\tau[/math]).

THE LEPTON CLASSIFICATION

Generation	Lepton	Q	[math]L_e[/math]	[math]L_\mu[/math]	[math]L_\tau[/math]	Mass([math]\frac{MeV}{c^2}[/math])
Generation 1	e	-1	1	0	0	0.511003
Generation 1	[math]\nu_e[/math]	0	1	0	0	0
Generation 2	[math]\mu[/math]	-1	0	1	0	105.659
Generation 2	[math]\nu_\mu[/math]	0	0	1	0	0
Generation 3	[math]\tau[/math]	-1	0	0	1	1784
Generation 3	[math]\nu_\tau[/math]	0	0	0	1	0

There are six anti leptons and anti quarks, all signs in the above tables would be reversed for them. Also, quarks and anti quarks can carry three color charges(red, green and ) that enables them to participate in strong interactions.

In the Standard Model the mediator elementary particles with spin-1 are bosons.
- The electromagnetic interaction is mediated by the photons, which are massless.
- The [math]W^+[/math], [math]W^-[/math] and [math]Z^0[/math] gauge bosons mediate the weak nuclear interactions between particles of different flavors.
- The gluons mediate the strong nuclear interaction between quarks.

THE MEDIATOR CLASSIFICATION

Mediator	Q(charge)	Mass([math]\frac{MeV}{c^2}[/math])	Force
gluon	0	0	strong
photon [math]\gamma[/math]	0	0	electromagnetic
[math]W^{+,-}[/math]	+1, -1	81,800	weak(charged)
[math]Z^0[/math]	0	92,600	weak(neutral)

The Quark Parton Model

In 1964, Gell-Mann and Zweig, against all experimental result, suggested that the fundamental triplet does exist and it contains three so called quarks. The quarks are the building blocks of the baryons and mesons and they cant be found in isolation. The quarks come with three different flavours: up([math]u[/math]), down([math]d[/math]) and strange([math]s[/math]) and their antiparticles. This set of three quarks corresponds to the fundamental SU(3) representation. The quantum numbers of quarks with their antiparticles are given in Table 1. The quarks carry electric charges [math]\pm \frac{2}{3}[/math] and [math]\pm \frac{1}{3}[/math] of the electron charge, which has never been observed before.

Quark	Spin	Parity	[math]e_{q}[/math]	[math]I[/math]	[math]I_{3}[/math]	S	B
[math]u[/math]	1/2	+1	+2/3	1/2	+1/2	0	+1/3
[math]d[/math]	1/2	+1	-1/3	1/2	-1/2	0	+1/3
[math]s[/math]	1/2	+1	-1/3	0	0	-1	+1/3
[math]\bar{u}[/math]	1/2	-1	-2/3	1/2	-1/2	0	-1/3
[math]\bar{d}[/math]	1/2	-1	+1/3	1/2	+1/2	0	-1/3
[math]\bar{s}[/math]	1/2	-1	+1/3	0	0	+1	-1/3

Table 1. Quarks in the Quark Model with their quantum numbers and electric charge n units of electron

Baryons are obtained by as a combination of three quarks([math]qqq[/math]) and mesons by combining a quark and an antiquark ([math]q\bar{q}[/math]). From the rules for combining representation of SU(3) one can show the patterns of baryons and mesons <ref name="Close">Close, F.E. (1979). An Introduction to Quarks and Patrons. London, UK: Academic Press Inc. LTD.</ref>:

[math]q\bar{q} = \bold{3} \otimes \bold{3} = 1 \oplus 8[/math]

[math]qqq = 3 \otimes 3 \otimes 3 = 1 \oplus 8 \oplus 8 \oplus 10[/math]

The constituent quark model describes a nucleon as a combination of three quarks. According to the quark model, two of the three quarks in a proton are labeled as having a flavor ``up" and the remaining quark a flavor ``down". The two up quarks have fractional charge [math]+\frac{2}{3}e[/math] while the down quark has a charge [math]-\frac{1}{3}e[/math]. All quarks are spin [math]\frac{1}{2}[/math] particles. In the quark model each quark carries one third of the nucleon mass.

Since late 1960, inelastic scattering experiments were used to probe a nucleon's excited states. Performed experiments suggested that the charge of the nucleon is distributed on a pointlike constituents of the nucleon. The experiments at the SLAC used high energy electrons scattered by nucleons, where virtual photon is the mediator between the target nucleon and coulomb scattering of an electron. The four-momentum, Q, of the virtual photon serves as a measure of the resolution of the scattering and may be formulated as:

[math]d = \frac{\hbar c}{Q} = \frac{0.2 \;\mbox {GeV} \cdot \mbox{ fm}}{Q}[/math] .

The electron scattering data taken during the SLAC experiments revealed a scaling behavior, which was later defined as Bjorken scaling. The inelastic cross section was anticipated to fall sharply with $Q^2$ like the elastic cross section. However, the observed limited dependence on [math]Q^2[/math] suggested that the nucleons constituents are pointlike dimensionless scattering centers. Independently, Richard Feynman introduced the quark parton model where the nucleons are constructed by three point like constituents, called partons.

Shortly afterwards, it was discovered that partons and quarks are the same particles. In the QPM the mass of the quark is much smaller than in the naive quark model. In the parton model the inelastic electron nucleon interaction via the virtual photon is understood as an incoherent elastic scattering processes between the electron and the constituents of the target nucleon. ``In other words, one assumes that a single interaction does not happen with the nucleon as a whole, but with exactly one of its constituents."<ref name="QCDHighEnergyExperimentsandTheory">Dissertori, G., Knowles, I.K., & Schmelling, M. (2003). Quantum Chromodynamics: High Energy Experiments and Theory. Oxford, UK: Oxford University Press.</ref> In addition, two categories of quarks were introduced, ``sea" and ``valence" quarks. The macroscopic properties of the particle are determined by its valence quarks. On the other hand, the so called sea quarks, virtual quarks and antiquarks, are constantly emitted and absorbed by the vacuum.

The inelastic scattering between the electron and the nucleon can be described by the two structure function, which only depend on [math]x_{B}[/math] Bjorken scaling variable - the fraction of nucleon four-momentum carried by the partons.

It was experimentally shown, that the measured croos section of inelastic lepton-nucleon scattering depends only on $x_{B}$, as it was mention above it is reffered as scaling. If there where additional objects inside the nucleon beside the main building partons, it would introduce new energy scale. The experimental observation of scaling phenomenon was the first evidence of the statement that the quarks are the constituents of the hadron. The results which were obtained from MIT-SLAC Collaboration(1970)are presented below on Figure 1 and 2 <ref name="QCDHighEnergyExperimentsandTheory">Dissertori, G., Knowles, I.K., & Schmelling, M. (2003). Quantum Chromodynamics: High Energy Experiments and Theory. Oxford, UK: Oxford University Press.</ref> <ref name="RobertsSpinStructure">Roberts, R. G. (1990). The structure of the proton. Cambridge Monographs on Mathematical Physics. Cambridge, UK: Cambridge University Press.</ref> . It clearly shows the structure function dependence on [math]x_{B}[/math] variable and independence of the four-momentum transfer squared.

200px

Figure 1. Scaling behavior of [math]\nu W_2(1/x_{B})=F_2(1/x_{B})[/math] for various [math]Q^{2}[/math] ranges.

Figure 2.Value of [math]\nu W_2(Q^{2})=F_2(Q^{2})[/math] for [math]x_B=0.25[/math] .

The quark parton model predictions are in agreement with the experimental results. One of those predictions is the magnet moments of baryons. For example, the magnet moment of the proton should be the sum of the magnetic moments of the constituent quarks according to the naive quark model <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> :

[math]\frac{e}{2m_p} \mu_p= \Sigma_{i=1,2,3} \lt P_{\frac{1}{2}}|\frac{e_q(i)\sigma_z(i)}{2m_p(i)}|P_{\frac{1}{2}}\gt [/math]

Assuming that the masses of light non-strange quarks are just one third of the total nucleon mass [math]m_d=m_u=\frac{m_p}{3}=\frac{m_n}{3}[/math] and expressing the magnetic moment in units of [math]\frac{e}{2m_p}[/math] we get the following result [math]\mu_p=3[/math], which agrees with the findings of experiment. In addition, the quark parton model predictions of magnetic moments of the other baryons are compared with the experimental results below in Table 2. As it can be observed, it is in agreement with the experiment within the accuracy of 20 - 25 [math]%[/math].

Particle	The Quark Model Prediction	Experimental Result
p	3	2.79
n	-2	-1.91
[math]\Lambda[/math]	-0.5	-0.61
[math]\Sigma^+[/math]	2.84	2.46
[math]\Sigma^-[/math]	-1.16	-1.16 [math]\pm[/math] 0.03
[math]\Xi^0[/math]	-1.33	-1.25[math] \pm[/math] 0.01
[math]\Xi^-[/math]	-0.33	-0.65 [math]\pm[/math] 0.04

Table 2. Magnetic moment of baryons in units of nuclear magnetons ([math]\frac{e}{2m_p}[/math]). <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref>

The Quark Parton Model was succesful explaining the mass of baryons. The baryon masses can be expressed in the quark model using the de Rujula-Georgi-Glashow approach:

[math]m_B = \Sigma_i m_q(i)+ b \Sigma_{i\neq j}\frac{\sigma(i)\sigma(j)}{m_q(i)m_q(j)}[/math]

The difference between the actual experimental results and the predictions is in order of 5 -6 MeV. On the other hand, the similar formula for meson masses fails. The difference in meson mass case, between the experiment and calculation is approximately 100 MeV. This can be explained, by calculating the average mass of the quark in a baryon and meson <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> :

[math]\lt m_q\gt _M = \frac{1}{2}(\frac{1}{4}m_\pi + \frac{3}{4}m_p)=303 MeV[/math]

[math]\lt m_q\gt _B = \frac{1}{3}(\frac{1}{2}m_N + \frac{1}{2}m_{\Delta})=363 MeV[/math]

Particle	Prediction ([math]MeV/c^{2}[/math])	Experiment ([math]MeV/c^{2}[/math])
N	930	940 [math]\pm[/math] 2
[math]\Delta[/math]	1230	1232 [math]\pm[/math] 2
[math]\Sigma[/math]	1178	1193 [math]\pm[/math] 5
[math]\Lambda[/math]	1110	1116 [math]\pm[/math] 1
[math]\Sigma^*[/math]	1377	1385 [math]\pm[/math] 4
[math]\Xi[/math]	1329	1318 [math]\pm[/math] 4
[math]\Xi^*[/math]	1529	1533 [math]\pm[/math] 4
[math]\Omega[/math]	1675	1672 [math]\pm[/math] 1

Table 3. Baryon mass predictions compared with experimental findings.<ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> <ref name="Camalich"> Camalich, J.M., Geng, L.S., & Vicente Vacas, M.J. (2010). The lowest-lying baryon masses in covariant SU(3)-flavor chiral perturbation theory. arXiv:1003.1929v1 [hep-lat]</ref>

Notes

<references/>

Semi Inclusive Deep Inelastic Scattering

Deep inelastic scattering (DIS) of leptons on nucleons is the most powerful experimental tool for the investigation of the structure of nucleons. In experiments both the charged (electrons, muons) and neutral (neutrinos) leptons are used with their antiparticles. In deep inelastic scattering the scattering occurs on a single nucleon or on a bound protons and neutrons inside the nucleus. At large momentum transfer the inelastic scattering is the incoherent sum of elastic scattering off the nucleon constituents, which are assumed to be dimensionless pointlike quarks. In the Constituent quark model (CQM) the constituents of the hadron are up and down quarks, whereas in the Quantum Chromodynamics the nucleon is a composition of quarks, antiquarks and gluons.

The polarized quark distribution functions can be extracted from SIDIS measurements using the quark flavor tagging method and exclude assumptions used in inclusive DIS measurements. In SIDIS the double spin asymmetry can be expressed in terms of the cross sections of final state hadrons produced in the experiment \cite{7} :

[math]A_1^h = \frac{\sigma_{1/2}^h - \sigma_{3/2}^h}{\sigma_{1/2}^h + \sigma_{3/2}^h}[/math]

where [math]\sigma_{1/2}^h[/math] ([math]\sigma_{3/2}^h[/math]) represents the semi inclusive cross section of type $h$ hadrons produced in the final state when the spin of the initial electron beam was antiparallel(parallel) to the target nucleon spin.

The semi-inclusive cross section can be expressed in terms of quark distribution functions and fragmentation functions:

[math] \frac{d^3 \sigma^h_{1/2(3/2)}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{+(-)}(x,Q^2)D_q^h(z,Q^2)[/math]

The measured structure function in inclusive deep inelastic scattering experiments contains the contribution from all the different quark flavors to the total nucleon momentum and spin, without distinguishing the contribution from the individual quark flavors. Semi inclusive deep inelastic scattering experiments provide an opportunity to determine the struck quark flavor by detecting the hadron in the final state in coincidence with an electron.

The kinematics of single pion electroproduction in SIDIS can be described by five variables: the virtual photon four-momentum transfered squared [math]Q^2[/math], invariant mass of the photon-nucleon system [math]W[/math], the polar [math]{\theta_{\pi}}^*[/math] and the azimuthal angle [math]{\varphi_{\pi}}^*[/math] of the outgoing pion in the center of mass frame, and the scattered electron azimuthal angle [math]{\varphi}_e[/math].

File:SIDISDiagram.jpg

Figure 1. Diagram of The Semi Inclusive Deep Inelastic Scattering \cite{7}

The incoming electron with four momentum [math]k = (E[/math], [math]\vec{k}[/math])$ is scattered from the target of four momentum ([math]M[/math], [math]\vec{0}[/math]), where [math]M[/math] represents the rest mass of the target nucleon. The four momentum of the scattered electron and hadron are respectively [math]k^{'}[/math] = ([math]E^{'}[/math], [math]\vec{k^{'}}[/math]) and [math]p_h[/math] = ([math]E_h[/math], [math]\vec{p_h}[/math]). Semi inclusive deep inelastic scattering is depicted in Figure. 1. The four momentum of the exchanged virtual photon, through which the SIDIS occurs, is the four momentum lost by the initial electron $q = k - k^'$. The negative square of the four momenta can be written as [math]Q^2 = - q^2|_{lab} = 4EE^{'}\sin^{2} \frac{\theta}{2}[/math], where [math]Q^2[/math] is greater then zero. The energy transferred from the scattering electron to the target nucleon, which is also the energy of the virtual photon, is given by

[math]\nu = \frac {P \cdot q}{M} = E - E^{'}|_{lab}[/math]

The Bjorken scaling variable x is defined as

[math]x = \frac {Q^2}{2 P q} = \frac {Q^2}{2M \nu}[/math]

The fraction of the virtual photon energy transferred to a hadron, that is detected in the final state in coincidence with the scattered electron, is

[math]z = \frac{P\cdot p_h}{P\cdot q} =^{lab} \frac{E_h}{\nu}[/math]

where the last kinematical variable is the invariant mass of the scattering process available to produce the final hadronic state

[math]W^2 = (q + P_h)^2 = M^2 + 2 M \nu -Q^2[/math]

Kinematic variables in deep inelastic scattering

Kinematic variable	Description
[math]k = (E, k)[/math], [math]k = (E^', k^')[/math]	4 - momenta of the initial and final state leptons
[math]\theta[/math], [math]\phi[/math]	Polar and azimuthal angle of the scattered lepton
[math]P^{lab} = (M, 0)[/math]	4 - momentum of the initial target nucleon
[math]q = k - k^'[/math]	4 - momentum of the virtual photon
[math]Q^2 = - {q^2} ^{lab} = 4EE^'\sin^2 \frac{\theta}{2}[/math]	Negative squared 4 - momentum transfer
[math]\nu = \frac {P q}{M} =^{lab} E - E^'[/math]	Energy of the virtual photon
[math]x = \frac {Q^2}{2 P q} = \frac {Q^2}{2M \nu}[/math]	Bjorken scaling variable
[math]y = \frac{Pq}{Pk} =^{lab} \frac{\nu}{E}[/math]	Fractional energy of the virtual photon
[math]W^2 = (P + q)^2 = M^2 + 2M\nu - Q^2[/math]	Squared invariant mass of the photon-nucleon system
[math]p = (E_h, p)[/math]	4 - momentum of a hadron in the final state
[math]z = \frac{Pp}{Pq} =^{lab} \frac{E_h}{\nu}[/math]	Fractional energy of the observed final state hadron

The electron scattering cross section off a nucleon can be written as \cite{6} :

[math]\frac{d^2 \sigma}{dQ^{2}dW^{2}} = \frac{2 \pi \alpha^2 M}{(s-M^2)^2Q^2} [2W_1 (W^2,Q^2) + W_2(W^2,Q^2)(\frac{(s-M^2)(s-W^2-Q^2)}{M^2Q^2}-1)][/math]

and in the target rest frame it can be expressed in terms of the initial and final energies of the electron and the electron scattering angle [math]\theta[/math]:

[math]\frac{d^2 \sigma}{d\Omega d E^{'}} = \frac{\alpha^{2} M}{8E^{2}E_p \sin^4\frac{\theta}{2}}[2W_1\sin^2\frac{\theta}{2} + W_2 \frac{4E^2_p}{M^2}\cos^2\frac{\theta}{2}][/math]

where [math]W_1[/math] and [math]W_2[/math] are so called structure functions, [math]E_p[/math] and [math]E[/math] the energy of the initial proton and electron respectively, [math]\theta[/math] the polar angle of the scattered electron. [math]M[/math] is the mass of the target, in our case the proton.

As it was mentioned above, the DIS interaction doesn't happen with the hadron as a whole, but with one of its constituents. Each quark(constituent) carries the fraction four-momentum [math]x[/math] of the nucleon with probability density [math]q(x)[/math]. [math]q(x)[/math] is the probability of finding the [math]q[/math]th quark with fraction [math]x[/math] of the nucleon four-momentum. Under these assumptions, the structure functions can be written as a sum of the elastic structure functions weighted by [math]q(x)[/math]. Taking into consideration that the mass of the [math]i[/math]th quark is also the fraction [math]x[/math] of the nucleon mass [math]M_q = x M_h[/math]:

[math]W_1(Q^2, \nu ) =\Sigma_q \int_0^1 dx q(x) e_q^2 \frac{Q^2}{4x^2 M_h^2} \delta (\nu - \frac{Q^2}{2M_hx}) = \Sigma_q e_q^2 q(x_B)\frac{1}{2M_h}[/math]

and

[math]W_2(Q^2, \nu ) =\Sigma_q \int_0^1 dx q(x) e_q^2 \delta (\nu - \frac{Q^2}{2M_hx}) = \Sigma_q e_q^2 q(x_B)\frac{x_B}{\nu}.[/math]

The DIS of the unpolarized electron by a nucleon can be described in terms of two structure functions, [math]F_1(x)[/math] and [math]F_2(x)[/math] where:

[math]F_1(x) = M_h W_1 = \frac{1}{2}\Sigma_q e_q^2q(x)[/math]

and

[math]F_2(x) = \nu W_2 = \frac{1}{2}\Sigma_q x e_q^2 q(x)[/math]

The relation between the structure functions [math]F_1(x)[/math] and [math]F_2(x)[/math] is given by the following equation:

[math]F_2(x) \frac{1+\gamma^2}{1+R} = 2 x F_1(x)[/math]

where [math]R(x,Q^2)[/math] is the ratio of longitudinal to transverse deep inelastic scattering cross sections and [math]\gamma = \sqrt{\frac{Q^2}{\nu^2}}[/math]. In the naive quark parton model the longitudinal-transverse interference is neglected. In the Bjorken limit it can be reduced to the Callan-Gross relation:

[math]F_2(x) = 2 x F_1(x)[/math]

The structure function [math]F_1[/math] measures the parton density, while [math]F_2[/math] describes the momentum density.

The distributions of up and down quarks in the nucleon are defined as [math]u(x)[/math] and [math]d(x)[/math]. There are two categories of quarks: valence and sea quarks [math]u(x) = u_v(x) + u_s(x)[/math], assuming that [math]u_s(x)=\bar{u}(x)[/math]. The constituent quark model (CQM or QPM) states that the proton(neutron) contains two up(down) quarks and one down(up) quark. Summing over all the constituents of a proton should result in the following sum rule:

[math]\int_0^1 dx u_v(x) = 2[/math]

and

[math]\int_0^1 dx d_v(x) = 1[/math]

The electromagnetic structure function for the proton and neutron can be expressed in terms of quark distribution functions:

[math]F_2^{ep} = \frac{4}{9}[xu(x) + x\bar{u}(x) + xc(x) + x\bar{c}(x)] + \frac{1}{9}[xd(x) + x\bar{d}(x) + xs(x) + x\bar{s}(x)][/math]

[math]F_2^{en}[/math] can be obtained from [math]F_2^{ep}[/math] by replacing [math]u[/math] [math]\rightarrow[/math] [math]d[/math] and vice versa. From the last two equations the structure functions for the proton and neutron can be written in terms of valence quark distribution functions:

[math]F_2^{ep} = x [ \frac{4}{9} u_v(x) + \frac{1}{9} d_v(x) ][/math]

and

[math]F_2^{en} = x [ \frac{4}{9} d_v(x) + \frac{1}{9} u_v(x) ][/math]

For most fixed-target experiments like EG1, the spin asymmetry is given by the ratio of the polarized structure function to the unpolarized: [math]A(x, Q^2) = \frac{g_1(x)}{F_1(x)}[/math], where the polarized structure function [math]g_1(x)[/math] represents the helicity difference of quark number densities. The spin asymmetry [math]A[/math] and the unpolarized structure function [math]F_1[/math] are measurable quantities and through them one can determine [math]g_1(x)[/math], which maybe expressed as :

[math]g_1(x) = \frac{1}{2} \Sigma_q e_q^2 (q^+(x) - q^-(x)) \equiv \frac{1}{2}\Sigma_q e_q^2 \Delta q(x)[/math]

where [math]q^{+(-)}(x)[/math] is the quark distribution function with spin oriented parallel(antiparallel) to the spin of nucleon.

Fragmentation Independence

The asymmetries from semi inclusive pion electroproduction using proton or deuteron targets can be written in terms of the difference of the yield from oppositely charged pions \cite{10} :

[math]A_{1,p}^{\pi^+ \pm \pi^-} = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-}} = \frac{[({\sigma_p}^{\pi^+})_{1/2}-({\sigma_p}^{\pi^+})_{3/2}] \pm [({\sigma_p}^{\pi^-})_{1/2}-({\sigma_p}^{\pi^-})_{3/2}]}{[({\sigma_p}^{\pi^+})_{1/2}+({\sigma_p}^{\pi^+})_{3/2}] \pm [({\sigma_p}^{\pi^-})_{1/2}+({\sigma_p}^{\pi^-})_{3/2}]}[/math]

[math]A_{1,2H}^{\pi^+ \pm \pi^-} = \frac{\Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_{2H}^{\pi^+ \pm \pi^-}} = \frac{[({\sigma_{2H}}^{\pi^+})_{1/2}-({\sigma_{2H}}^{\pi^+})_{3/2}] \pm [({\sigma_{2H}}^{\pi^-})_{1/2}-({\sigma_{2H}}^{\pi^-})_{3/2}]}{[({\sigma_{2H}}^{\pi^+})_{1/2}+({\sigma_{2H}}^{\pi^+})_{3/2}] \pm [({\sigma_{2H}}^{\pi^-})_{1/2}+({\sigma_{2H}}^{\pi^-})_{3/2}]}[/math]

Independent fragmentation identifies the process in which quarks fragment into hadrons, independent of the photon-quark scattering process. In other words, the fragmentation process is independent of the initial quark environment which initiates the hadronization process. Assuming independent fragmentation and using isospin and charge conjugation invariance for the fragmentation functions, the following equality holds:

[math]D_u^{\pi^+ \pm \pi^-} = D_u^{\pi^+} \pm D_u^{\pi^-} = D_d^{\pi^+ \pm \pi^-}[/math]

The polarized and unpolarized cross sections for pion electroproduction can be written in terms of valence quark distribution functions in the valence region as:

[math]\Delta \sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta d + \Delta d^-) \pm (\Delta u + \Delta u^-)]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

and unpolarized:

[math]\sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(d + \bar{d}) \pm (u + \bar{u})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

In the valence region ([math]x_{B}\gt 0.3[/math]), where the sea quark contribution is minimized, the above asymmetries can be expressed in terms of polarized and unpolarized valence quark distributions:

[math]A_{1,p}^{\pi^+ \pm \pi^-} = \frac{4 \Delta u_v(x) \pm \Delta d_v(x)}{4u_v(x) \pm d_v(x)}[/math]

[math]A_{1,2H}^{\pi^+ \pm \pi^-} = \frac{\Delta u_v(x) + \Delta d_v(x)}{u_v(x) + d_v(x)}[/math]

The ratio of polarized to unpolarized valence up and down quark distributions may then be written as

[math]\frac{\Delta u_v}{u_v}(x,Q^2) = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-} + \Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-} + \sigma_{2H}^{\pi^+ \pm \pi^-}} (x,Q^2)[/math]

and

[math]\frac{\Delta d_v}{d_v}(x,Q^2) = \frac{\Delta \sigma_p^{\pi^+ \pm \pi^-} - 4\Delta \sigma_{2H}^{\pi^+ \pm \pi^-}}{\sigma_p^{\pi^+ \pm \pi^-} - 4\sigma_{2H}^{\pi^+ \pm \pi^-}} (x,Q^2)[/math]

The ratio of polarized to unpolarized valence quark distribution functions can be extracted using the last two equations.

Independent Fragmentation Function Test

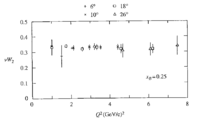
A test of independent fragmentation can be performed with polarized proton and neutron targets. The ratio of the difference of polarized to unpolarized cross sections for proton and neutron targets [math]\Delta R_{np}^{\pi^+ + \pi^-}[/math] can be written in terms of the structure functions:

[math]\Delta R_{np}^{\pi^+ + \pi^-} = \frac{\Delta \sigma_p^{\pi^+ + \pi^-} - \Delta \sigma_{n}^{\pi^+ + \pi^-}}{\sigma_p^{\pi^+ + \pi^-} - \sigma_{n}^{\pi^+ + \pi^-}}=[/math]

\frac{(\Delta u +\Delta \bar{u}) - (\Delta d + \Delta \bar{d})}{(u+\bar{u}) - (d+\bar{d})}(x,Q^2)

\]

\[ = \frac{g_1^p - g_1^n}{F_1^p - F_1^n}(x,Q^2) \]

The last expression of the asymmetry $\Delta R_{np}^{\pi^+ + \pi^-}$ was obtained from the following equations:

\[ g_1^p - g_1^n = \frac{1}{6}[(\Delta u +\Delta \bar{u}) - (\Delta d + \Delta \bar{d})] \]

and

\[ F_1^p - F_1^n = \frac{1}{6}[(u+\bar{u}) - (d+\bar{d})] \] Independent fragmentation holds if the ratio of the difference of polarized to unpolarized cross sections for proton and neutron targets $\Delta R_{np}^{\pi^+ + \pi^-}$ depends only on $x$ and $Q^2$ of the quantities $g_1$ and $F_1$ measured in deep inelastic scattering and is independent of $z$.