Tamar Thesis TheoryChapt
Introduction
The understanding of the spin structure in the nucleon remains a major challenge for hadron physics. The parton model predicted that quarks carry about (67 7)% of the total nucleon spin. Experiments performed at the European Organization for Nuclear Research(CERN) by Electromagnetic Compatibility collaboration(EMC) found out that only (31 7)% of the nucleon spin is carried by the quarks. Other experiments at CERN(spin muon collaboration(SMC)) and SLAC(E142 && E143) did not agree with the naive quark parton model <ref name="EllisKarline"> Ellis, J., & Karline, M.(1965). Determination of and the Nucleon Spin Decomposition using Recent Polarized Structure Function Data. Phys. Lett., B(341), pg 397.</ref>. This reduction is assumed to be the caused by a negatively polarized quark sea at low momentum fraction x, which is not considered in quark models. The complete picture of the nucleon spin can be obtained by taking into account the spin contributions from the gluons, the sea quarks and in addition the quarks orbital momentum. So the spin of the nucleon can be written as the sum of the following terms<ref>B. Hommez, Ph.D Thesis, University of Gent (2003).</ref>:
where - is the spin contribution from the quarks, - from the gluons and - the orbital angular momentum contribution from the partons(quarks). The spin contribution from each type of quark to the total nucleon spin is following<ref name="EllisKarline"> Ellis, J., & Karline, M.(1965). Determination of and the Nucleon Spin Decomposition using Recent Polarized Structure Function Data. Phys. Lett., B(341), pg 397.</ref>:
The Standard Model
Matter is composed of two types of elementary particles, quarks and leptons, which form composite particles by exchanging bosons, yet another elementary particle. The Standard Model of particle physics, a Quantum Field Theory, was developed between 1970 and 1973. The Standard Model describes all of the known elementary particle interactions except gravity. It is the collection of the following related theories: quantum electrodynamics, the Glashow-Weinberg-Salam theory of electroweak processes and quantum chromodynamics.
The Standard Model describes a nucleon, a neutron or proton, as a particle composed of 3 constituent quarks having a flavor of either up or down. Quarks are spin 1/2 particles with fractional charge() and come in the flavors of strangeness(S), charm(C), beauty(B) and truth(T) in addition to up (u) and down(d). Quarks have Baryon quantum number () of 1/3. The quantum numbers of quarks with their antiparticles are given in Table 1.
| Quark | Spin | (electric charge) | (Isospin) | (Baryon Number) | C(Charmness) | S(Strangeness) | T(Topness) | B(Bottomness) | Antiquark |
|---|---|---|---|---|---|---|---|---|---|
| (up) | 1/2 | +2/3 | +1/2 | +1/3 | 0 | 0 | 0 | 0 | |
| (down) | 1/2 | -1/3 | -1/2 | +1/3 | 0 | 0 | 0 | 0 | |
| (charm) | 1/2 | +2/3 | 0 | +1/3 | +1 | 0 | 0 | 0 | |
| (strange) | 1/2 | -1/3 | 0 | +1/3 | 0 | -1 | 0 | 0 | |
| (top) | 1/2 | +2/3 | 0 | +1/3 | 0 | 0 | +1 | 0 | |
| (bottom) | 1/2 | -1/3 | 0 | +1/3 | 0 | 0 | 0 | -1 |
| Table 1. Quarks in the Quark Model with their quantum numbers and electric charge in units of electron. |
The Quark Parton Model
In 1964 Gell-Mann and Zweig suggested that a proton was composed of point like particles in an effort to explain the resonance spectra observed by experiments in the 1950s. <ref name="Bloom1968">Bloom, E. et al., SLAC Group A, reported byW. K. Panofsky in Int. Conf. on High Energy Phys., Vienna, 1968 CERN, Geneva (1968) p.23</ref> These point like particles, referred to as partons and later quarks, have not been observed as free particles and are the building blocks of baryons and mesons. The model assumes that partons are identified according to a quantum number called flavor which contains three values: up(), down() and strange() and their antiparticles. This set of flavor quantum numbers can be used within the context of group theory's SU(3) representation to construct isospin wave functions for the nucleon. <ref name="Close">Close, F.E. (1979). An Introduction to Quarks and Patrons. London, UK: Academic Press Inc. LTD.</ref>
The constituent quark model describes a nucleon as a combination of three quarks. According to the quark model, two of the three quarks in a proton are labeled as having a flavor ``up" and the remaining quark a flavor ``down". The two up quarks have fractional charge while the down quark has a charge . All quarks are spin particles. In the quark model each quark carries one third of the nucleon mass.
Since the late 1960s, inelastic scattering experiments have been used to probe a nucleon's excited states. The experiments suggested that the charge of the nucleon is distributed among pointlike constituents of the nucleon. The experiments at the Stanford Linear Accelerator Center (SLAC) used high 19.5 GeV energy electrons coulomb scattered by nucleons through the exchange of a virtual photon. The spacial resolution (d) available using the electron probe may be written in terms of the exchanged virtual photon's four-momentum, Q, such that the electron probe's ability to resolve the contituents of a proton increases as the four momentuum increased according to
| . |
where
The electron scattering data taken during the SLAC experiments revealed a scaling behavior, which was later defined as Bjorken scaling. The inelastic cross section was anticipated to fall sharply with like the elastic cross section. However, the observed limited dependence on suggested that the nucleons constituents are pointlike dimensionless scattering centers.
Independently, Richard Feynman introduced the quark parton model where the nucleons are constructed by three point like constituents, called partons. Shortly afterwards, it was discovered that partons and quarks are the same particles. In the QPM, the mass of the quark is much smaller than in the naive quark model. In the parton model, the inelastic electron nucleon interaction via the virtual photon is understood as an incoherent elastic scattering processes between the electron and the constituents of the target nucleon. In other words, a single interaction does not happen with the nucleon as a whole, but with exactly one of its constituents.<ref name="QCDHighEnergyExperimentsandTheory">Dissertori, G., Knowles, I.K., & Schmelling, M. (2003). Quantum Chromodynamics: High Energy Experiments and Theory. Oxford, UK: Oxford University Press.</ref> In addition, two categories of quarks were introduced, ``sea" and ``valence" quarks. The macroscopic properties of the particle are determined by its valence quarks. On the other hand, the so called sea quarks, virtual quarks and antiquarks, are constantly emitted and absorbed by the vacuum.
The inelastic scattering between the electron and the nucleon can be described by the two structure functions, which only depend on Bjorken scaling variable - the fraction of the nucleon four-momentum carried by the partons. It was experimentally shown, that the measured cross section of inelastic lepton-nucleon scattering depends only on , as it was mentioned above it is reffered as scaling. If there where additional objects inside the nucleon besides the main building partons, it would introduce new energy scales. The experimental observation of scaling phenomenon was the first evidence of the statement that the quarks are the constituents of the hadron. The results which were obtained from MIT-SLAC Collaboration(1970) are presented below on Figure 1 and 2 <ref name="QCDHighEnergyExperimentsandTheory">Dissertori, G., Knowles, I.K., & Schmelling, M. (2003). Quantum Chromodynamics: High Energy Experiments and Theory. Oxford, UK: Oxford University Press.</ref> <ref name="RobertsSpinStructure">Roberts, R. G. (1990). The structure of the proton. Cambridge Monographs on Mathematical Physics. Cambridge, UK: Cambridge University Press.</ref> . It clearly shows the structure function dependence on variable and independence of the four-momentum transfer squared.
| 200px |
| Figure 1. Scaling behavior of for various ranges. |
|
| Figure 2.Value of for . |
The quark parton model predictions are in agreement with the experimental results. One of those predictions is the magnet moment of baryons. For example, the magnet moment of the proton should be the sum of the magnetic moments of the constituent quarks according to the naive quark model <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> :
Assuming that the masses of light non-strange quarks are just one third of the total nucleon mass and expressing the magnetic moment in units of we get the following result , which agrees with experimental findings. In addition, the quark parton model predictions of magnetic moments of the other baryons are compared with the experimental results below in Table 2. As it can be observed, it is in agreement with the experiment within the accuracy of 20 - 25 .
| Particle | The Quark Model Prediction | Experimental Result |
|---|---|---|
| p | 3 | 2.79 |
| n | -2 | -1.91 |
| -0.5 | -0.61 | |
| 2.84 | 2.46 | |
| -1.16 | -1.16 0.03 | |
| -1.33 | -1.25 0.01 | |
| -0.33 | -0.65 0.04 |
| Table 2. Magnetic moment of baryons in units of nuclear magnetons (). <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> |
The Quark Parton Model was succesful explaining the mass of baryons. The baryon masses can be expressed in the quark model using the de Rujula-Georgi-Glashow approach:
The difference between the actual experimental results and the predictions is in order of 5 -6 MeV. However, the similar formula for meson masses fails. The difference in meson mass case, between the experiment and calculation is approximately 100 MeV. This can be explained, by calculating the average mass of the quark in a baryon and meson <ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> :
| Particle | Prediction () | Experiment () |
|---|---|---|
| N | 930 | 940 2 |
| 1230 | 1232 2 | |
| 1178 | 1193 5 | |
| 1110 | 1116 1 | |
| 1377 | 1385 4 | |
| 1329 | 1318 4 | |
| 1529 | 1533 4 | |
| 1675 | 1672 1 |
| Table 3. Baryon mass predictions compared with experimental findings.<ref name="Anisovich">Anisovich, V.V., Kobrinsky, M.N., Nyiri, J., & Shabelski, Yu. M. (2004). Quark Model and High Energy Collisions. World Scientific Publishing Co. Pte. Ltd.</ref> <ref name="Camalich"> Camalich, J.M., Geng, L.S., & Vicente Vacas, M.J. (2010). The lowest-lying baryon masses in covariant SU(3)-flavor chiral perturbation theory. arXiv:1003.1929v1 [hep-lat]</ref> |
Lattice QCD
Although the Quark Model successfully described several nucleon properties, it was not a fundamental theory opening the doorway for the development of new field theory called Quantum Chromodynamics. In the Quark Model, the particles of the baryon decuplet are symmetric in spin and flavor, so that the wave functions that describe the fermions are fully symmetric and identical, which is a violation of the Pauli principle. As a solution, the Quantum Chromodynamics suggested that quarks carry additional degree of freedom "color". Quarks have three degrees of freedom: spin, flavour and color. There are three states of color: red, green and blue.
Deep inelastic lepton nucleon scattering experiments gave us an opportunity to measure the momentum weighted probability density function of partons in the proton and neutron. The fraction of the nucleon momentum carried by the quarks can be calculated by integrating the probability density function:
The last expression shows that the quarks inside the nucleon carry about of the total momentum. It leads to the question, are quarks the only particles inside the nucleon? In addition to the quarks and antiquarks, there are other components in the nucleon. They cant be seen by using electromagnetic (electron) and weak (neutrino) probe, because they do not carry weak or electric charge.
The scaling behavior was given by assumption that the nucleon is built by non-interacting pointlike quarks and antiquarks. However, by increasing the four-momentum transferred squared one can see that inside the nucleon there are more components then just three charged quarks.
| 350px |
| Figure 3. Scaling violation. |
It was concluded, that a nucleon consists of three main quarks so called "valence" quarks, which carry the quantum numbers of the nucleon and a "sea" of quark-antiquark pairs. The interaction between the quark-antiquark are mediated by the gluons. Unlike QED, where photon doesn't carry the charge, in QCD, gluon has a color charge and they can interact with each other. In other words, QCD is a theory where a field quanta is at the same time a field source. That makes QCD a non-Abelian field theory. QCD allows the following interactions
The colors carried by the eight gluons are following: , , , , , , , . The color is not experimentally observable, only "colorless" quark antiquark systems are observed: baryons(qqq), mesons() and antibaryons().
The confinement of the quark antiquark system can be explained by the fact that color force increases with the separation increase. As separation decreases the force becomes so that the quarks no longer interact. This phenomenon is referred as an asymptotic freedom. The strong coupling in QCD is defined to first order the following way:
where is found experimentally and is the number of active quark flavors. At , the quark confinement takes place.
Rewrite
The perturbative QCD is used to describe the deep inelastic scattering, because of incapacity to calculate more than a few non-perturbative quantities within the QCD. "The two most striking features of QCD are confinement and asymptotic freedom, and both are somehow related to the running of the coupling constant, a feature of all quantum field theories.
Confinement. All observed particles are colourless: as two colour charges move apart, their interaction grows strong enough to create colour-anticolour pairs from the vacuum.These colour charges recombine with the original charges to form colourless objects in a process called hadronization. Thus, confinement is related to the rising of the coupling constant as the distance between charges becomes large, or equivalently as the energy scale Q2 goes to zero.
Asymptotic freedom. The interaction between quarks asymptotically tends to zero as the distance between quarks goes to zero. As a consequence, quarks in the nucleon can be considered free particles. Thus, asymptotic freedom is related to the falling of the coupling constant as the distance between charges becomes small, or equivalently as the energy scale Q2 goes to infinity."
Semi Inclusive Deep Inelastic Scattering
Deep inelastic scattering (DIS) of leptons on nucleons is the most powerful experimental tool for the investigation of the structure of nucleons. In experiments, both the charged (electrons, muons) and neutral (neutrinos) leptons are used with their antiparticles. In deep inelastic scattering, the scattering occurs on a single nucleon or on a bound protons and neutrons inside the nucleus. At large momentum transfer the inelastic scattering is the incoherent sum of elastic scattering off the nucleon constituents, which are assumed to be dimensionless pointlike quarks. In the Constituent quark model (CQM) the constituents of the hadron are up and down quarks, whereas in the Quantum Chromodynamics the nucleon is a composition of quarks, antiquarks and gluons. In inclusive deep inelastic scattering (IDIS), only the electron is detected in the final state, whereas in the case of semi inclusive deep inelatic scattering (SIDIS), a hadron is detected in coincidence with the scattered electron. Both physics processes can be characterized by the differential cross section. The cross section is proportional to the detection rate. The differential cross section for inclusive deep inelastic scattering can be written in terms of a lepton and a hadronic tensor <ref name="RobertsSpinStructure">Roberts, R. G. (1990). The structure of the proton. Cambridge Monographs on Mathematical Physics. Cambridge, UK: Cambridge University Press.</ref> :
where
and
the leptonic tensor describes the coupling between the scattering lepton and the virtual photon. The hadronic tensor describes the absorption of the virtual photon by the target nucleon. The hadronic tensor contains information about the nucleon structure. It can be written in terms of structure functions using symmetry arguments and conservation laws. However, the information about the spin distribution inside the nucleon is contained in the asymmetric part of the hadronic tensor, which can be obtained by taking the difference of the cross sections with opposite spin states of the initial electron beam.
The polarized quark distribution functions can be extracted from SIDIS measurements using the quark flavor tagging method and exclude assumptions used in inclusive DIS measurements. In SIDIS the double spin asymmetry can be expressed in terms of the cross sections of final state hadrons produced in the experiment <ref name="Airapetian"> Airapetian, A., et al. (The HERMES Collaboration). (2005). Quark helicity distributions in the nucleon for up, down, and strange quarks from semi-inclusive deep inelastic scattering. Phys. Rev.,
D(71), 012003.</ref>:
where () represents the semi inclusive cross section of type hadrons produced in the final state, when the spin of the initial electron beam was antiparallel(parallel) to the target nucleon spin.
The semi-inclusive cross section can be expressed in terms of quark distribution functions and fragmentation functions:
The measured structure function in inclusive deep inelastic scattering experiments contains the contribution from all the different quark flavors to the total nucleon momentum and spin, without distinguishing the contribution from the individual quark flavors. On the other hand, semi inclusive deep inelastic scattering experiments provide an opportunity to determine the struck quark flavor by detecting the hadron in the final state in coincidence with the scattered electron.
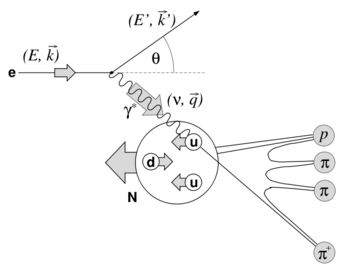
The kinematics of single pion electroproduction in SIDIS can be described by five variables: the virtual photon four-momentum transfered squared , invariant mass of the photon-nucleon system , the polar and the azimuthal angle of the outgoing pion in the center of mass frame, and the scattered electron azimuthal angle .
The incoming electron with four momentum , ) is scattered from the target of four momentum (, ), where represents the rest mass of the target nucleon. The four momentum of the scattered electron and hadron are respectively = (, ) and = (, ). Semi inclusive deep inelastic scattering is depicted in Fig.4. The four momentum of the exchanged virtual photon, through which the SIDIS occurs, is the four momentum lost by the initial electron . The negative square of the four momenta can be written as , where is greater then zero. The energy transferred from the scattering electron to the target nucleon, which is also the energy of the virtual photon, is given by
The Bjorken scaling variable x is defined as
The fraction of the virtual photon energy transferred to a hadron, that is detected in the final state in coincidence with the scattered electron, is
where the last kinematical variable is the invariant mass of the scattering process available to produce the final hadronic state
| Kinematic variable | Description |
|---|---|
| , | 4 - momenta of the initial and final state leptons |
| , | Polar and azimuthal angle of the scattered lepton |
| 4 - momentum of the initial target nucleon | |
| 4 - momentum of the virtual photon | |
| Negative squared 4 - momentum transfer | |
| Energy of the virtual photon | |
| Bjorken scaling variable | |
| Fractional energy of the virtual photon | |
| Squared invariant mass of the photon-nucleon system | |
| 4 - momentum of a hadron in the final state | |
| Fractional energy of the observed final state hadron |
| Table 4. Kinematic variables in deep inelastic scattering. |
The electron scattering cross section off a nucleon can be written as <ref name="RobertsSpinStructure">Roberts, R. G. (1990). The structure of the proton. Cambridge Monographs on Mathematical Physics. Cambridge, UK: Cambridge University Press.</ref> :
where
and in the target rest frame it can be expressed in terms of the initial and final energies of the electron and the electron scattering angle :
where and are so called structure functions, and the energy of the initial proton and electron respectively, the polar angle of the scattered electron. is the mass of the target, in our case the proton.
As it was mentioned above, the DIS interaction doesn't happen with the hadron as a whole, but with one of its constituents. Each quark (constituent) carries the fraction four-momentum of the nucleon with probability density . is the probability of finding the th quark with fraction of the nucleon four-momentum. Under these assumptions, the structure functions can be written as a sum of the elastic structure functions weighted by . Taking into consideration that the mass of the th quark is also the fraction of the nucleon mass :
and
The DIS of the unpolarized electron by a nucleon can be described in terms of two structure functions, and
|
|
and
The structure function measures the parton density, while describes the momentum density. The relation between the structure functions and is given by the following equation:
where is the ratio of longitudinal to transverse deep inelastic scattering cross sections and . In the naive quark parton model, the longitudinal-transverse interference is neglected. In the Bjorken limit it can be reduced to the Callan-Gross relation:
The distributions of up and down quarks in the nucleon are defined as and . There are two categories of quarks: valence and sea quarks , assuming that . The constituent quark model (CQM or QPM) states that the proton(neutron) contains two up(down) quarks and one down(up) quark. Summing over all the constituents of a proton should result in the following sum rule:
and
The electromagnetic structure function for the proton and neutron can be expressed in terms of the quark distribution functions:
can be obtained from by replacing and vice versa.
From the last two equations, the structure functions for the proton and neutron can be written in terms of the valence quark distribution functions:
and
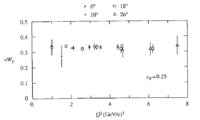
For most fixed-target experiments like EG1, the spin asymmetry is given by the ratio of the polarized structure function to the unpolarized: , where the polarized structure function represents the helicity difference of quark number densities. The spin asymmetry and the unpolarized structure function are measurable quantities and through them one can determine , which maybe expressed as:
where is the quark distribution function with spin oriented parallel(antiparallel) to the spin of the nucleon.
Fragmentation Independence
The asymmetries from semi inclusive pion electroproduction using proton or deuteron targets can be written in terms of the difference of the yield from oppositely charged pions <ref name="Christova"> Christova, E., & Leader, E. (1999). Semi-inclusive production-tests for independent fragmentation and for polarized quark densities. hep-ph/9907265.</ref>:
Independent fragmentation identifies the process in which quarks fragment into hadrons, independent of the photon-quark scattering process. In other words, the fragmentation process is independent of the initial quark environment, which initiates the hadronization process. Assuming independent fragmentation and using isospin ( and ) and charge () conjugation invariance for the fragmentation functions, the following equality holds:
The polarized and unpolarized cross sections for pion electroproduction can be written in terms of valence quark distribution functions in the valence region as:
and unpolarized:
In the valence region (), where the sea quark contribution is minimized, the above asymmetries can be expressed in terms of polarized and unpolarized valence quark distributions:
The ratio of polarized to unpolarized valence up and down quark distributions may then be written as
and
The ratio of polarized to unpolarized valence quark distribution functions can be extracted using the last two equations.
Independent Fragmentation Function Test
A test of independent fragmentation can be performed with polarized proton and neutron targets. The ratio of the difference of polarized to unpolarized cross sections for proton and neutron targets ( ) can be written in terms of the structure functions:
The last expression of the asymmetry was obtained from the following equations:
and
Independent fragmentation holds, if the ratio of the difference of polarized to unpolarized cross sections for proton and neutron targets depends only on Bjorken scaling variable () and four momentum transferred squared () of the quantities and measured in deep inelastic scattering and is independent of the fractional energy of the observed final state hadron ().
Notes
<references/>