Difference between revisions of "Se170063 Thin Window Analysis"
| (134 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | In order to try to pin down the ratio of pure selenium to the selenium in the soil, try using a 2 channel window to find the signal. The | + | In order to try to pin down the ratio of pure selenium to the selenium in the soil, try using a 2 channel window to find the signal. The uncertainty in the number of counts in the signal will be determined by subtracting the counts from the 2 channel window from the counts from a window expanded by 1 standard deviation, then divided by the original number of counts in the 2 channel window. Since the max value is fixed, it does not appear in the stats box, but I have included it in the table. It would seem that widening the gaussian function by half of its standard deviation yields results that agree up to 3 digits after the decimal with the result of widening the gaussian by its standard deviation. This would imply not much has changed between these methods. |
| + | Changes Made to table: | ||
| + | 12/14: Error in signal changed to <math> \sigma_I = I_{Expanded} - I </math> (try to not underestimate error) This includes changing the expanded window to a window expanded off of the 2 channel window | ||
{| border="3" cellpadding="5" cellspacing="0" | {| border="3" cellpadding="5" cellspacing="0" | ||
| Line 10: | Line 12: | ||
||Original Window ||[[File:170063 PureSe 400 640Sec OGWindow.png|100px]] || [[File:170063 PureSe 1100 1360 Seconds OGWindow.png|100px]] || [[File:170063 PureSeSpec 1875 2150Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 2650 2930Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 3400 3690Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 4120 4400Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 4840 5130 OGWindow.png|100px]] | ||Original Window ||[[File:170063 PureSe 400 640Sec OGWindow.png|100px]] || [[File:170063 PureSe 1100 1360 Seconds OGWindow.png|100px]] || [[File:170063 PureSeSpec 1875 2150Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 2650 2930Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 3400 3690Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 4120 4400Sec OGWindow.png|100px]] || [[File:170063 PureSeSpec 4840 5130 OGWindow.png|100px]] | ||
|- | |- | ||
| − | ||Expanded Window || [[File:170063 PureSe 400 640Sec ExpWindow.png|100px]] || [[File:170063 | + | ||Expanded Window || [[File:170063 PureSe Spect 400 640Sec ExpWindow.png|100px]] || [[File:170063 PureSeSpec 1100 1360 ExpWindow 1 11.png|100px]] || [[File:170063 PureSeSpec 1875 2150 ExpWidnow 1 11.png|100px]] || [[File:170063 PureSeSpec 2650 2930 ExpWindow 1 11.png|100px]] ||[[File:170063 PureSeSpec 3400 3940 ExpWindow 1 11.png|100px]] || [[File:170063 PureSeSpec 4120 4400 ExpWindow 1 11.png|100px]] || [[File:170063 PureSeSpec 4840 5130 ExpWindow 1 11.png|100px]] |
|- | |- | ||
||Maximum of Histogram|| 260980 || 241756 || 220348 || 191476 || 165549 || 139528 || 130930 | ||Maximum of Histogram|| 260980 || 241756 || 220348 || 191476 || 165549 || 139528 || 130930 | ||
| Line 22: | Line 24: | ||
||Integrated Background || 21120 +/- 103.16 || 21120 +/- 102.82 || 18992 +/- 97.8 || 17796 +/- 94.2 || 18836 +/- 96.4 || 14970 +/- 86 || 14322 +/- 68.4 | ||Integrated Background || 21120 +/- 103.16 || 21120 +/- 102.82 || 18992 +/- 97.8 || 17796 +/- 94.2 || 18836 +/- 96.4 || 14970 +/- 86 || 14322 +/- 68.4 | ||
|- | |- | ||
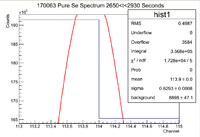
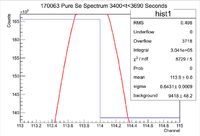
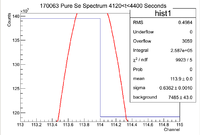
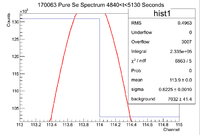
| − | ||Signal in Thin Window || 466700 | + | ||Signal in Thin Window || 466700 || 444100 || 412800 || 356800 || 304100 || 258700 || 233500 |
|- | |- | ||
| − | ||Background Subtracted Signal || 445580 +/- | + | ||Signal In Expanded Window || 515800 || 487300 || 452200 ||391400 || 340200 || 286800 || 258400 |
| + | |- | ||
| + | ||Error in Signal || 49100 || 43200 || 39400 ||34600 || 36100 || 28100 || 24900 | ||
| + | |- | ||
| + | ||Signal In Thin Window w/ Error || 466700 +/- 49100 || 444100 +/- 43200 || 412800 +/- 39400 || 356800 +/- 34600 || 304100 +/- 36100 || 258700 +/- 28100 || 233500 +/- 24900 | ||
| + | |- | ||
| + | ||Background Subtracted Signal || 445580 +/- 49100 || 422980 +/- 43200 || 393808 +/- 39400 || 339004 +/- 34600 || 285264 +/- 36100 || 243730 +/- 28100 || 219178 +/- 24900 | ||
|- | |- | ||
||Time Correction Factor (Sec) || 400 || 370 || 395 || 400 || 350 || 345 || 360 | ||Time Correction Factor (Sec) || 400 || 370 || 395 || 400 || 350 || 345 || 360 | ||
| Line 46: | Line 54: | ||
||Original Window || [[File:170063 MixSpec 0 300 OGWindow.png|100px]] || [[File:170063 MixSpec 730 1020Sec OGWindow.png|100px]] || [[File:170063 MixSpec 1480 1775Sec OGWindow.png|100px]] || [[File:170063 MixSpec 2250 2550Sec OGWindow.png|100px]] || [[File:170063 MixSpec 3050 3300Sec OGWindow.png|100px]] || [[File:170063 MixSpec 3775 4050Sec OGWindow.png|100px]] || [[File:170063 MixSpec 4480 4770Sec OGWindow.png|100px]] | ||Original Window || [[File:170063 MixSpec 0 300 OGWindow.png|100px]] || [[File:170063 MixSpec 730 1020Sec OGWindow.png|100px]] || [[File:170063 MixSpec 1480 1775Sec OGWindow.png|100px]] || [[File:170063 MixSpec 2250 2550Sec OGWindow.png|100px]] || [[File:170063 MixSpec 3050 3300Sec OGWindow.png|100px]] || [[File:170063 MixSpec 3775 4050Sec OGWindow.png|100px]] || [[File:170063 MixSpec 4480 4770Sec OGWindow.png|100px]] | ||
|- | |- | ||
| − | ||Expanded Window || [[File:170063 MixSpec 0 | + | ||Expanded Window || [[File:170063 MixSpec 0 300 ExpWindow 1 11.png|100px]] || [[File:170063 MixSpec 730 1020 ExpWindow 1 11.png|100px]] || [[File:170063 MixSpec 1480 1775 ExpWindow 1 11.png|100px]] || [[File:170063 MixSpec 2250 2550 ExpWindow 1 11.png|100px]] || [[File:170063 MixSpec 3050 3300 ExpWindow 1 11.png|100px]] || [[File:170063 MixSpec 3775 4050 ExpWindow 1 11.png|100px]] ||[[File:170063 MixSpec 4480 4770 ExpWindow 1 11.png|100px]] |
|- | |- | ||
||Maximum of Histogram|| 173289 || 155770 || 135740 || 124656 || 88582 || 80993 || 77781 | ||Maximum of Histogram|| 173289 || 155770 || 135740 || 124656 || 88582 || 80993 || 77781 | ||
| Line 58: | Line 66: | ||
||Integrated Background || 58880 +/- 169.86 || 41160 +/- 140.62 || 32840 +/- 131.04 || 28920 +/- 116.94 || 21900 +/- 101.3 || 21060 +/- 99.8 || 19618 +/- 96.4 | ||Integrated Background || 58880 +/- 169.86 || 41160 +/- 140.62 || 32840 +/- 131.04 || 28920 +/- 116.94 || 21900 +/- 101.3 || 21060 +/- 99.8 || 19618 +/- 96.4 | ||
|- | |- | ||
| − | ||Signal in Thin Window || 342200 | + | ||Signal in Thin Window || 342200 ||300100 || 267200 || 238600 || 170100 || 153200 || 147900 |
|- | |- | ||
| − | ||Background Subtracted Signal || 283320 +/- | + | ||Signal In Expanded Window ||423600 || 357800 || 312800 || 277700 || 198600 || 181200 || 174300 |
| + | |- | ||
| + | ||Error In Signal || 81400 || 57700 || 45600 || 39100 || 28500 || 28000 || 26400 | ||
| + | |- | ||
| + | ||Signal with Error || 342200 +/- 81400 || 300100 +/- 57700 || 267200 +/- 45600 || 238600 +/- 39100 || 170100 +/- 28500 || 153200 +/- 28000 || 147900 +/- 26400 | ||
| + | |- | ||
| + | ||Background Subtracted Signal || 283320 +/- 81400 || 258940 +/- 57700 || 234360 +/- 45600 || 209680 +/- 39100 || 148200 +/- 28500 || 132140 +/- 28000 || 128282 +/- 26400 | ||
|- | |- | ||
||.dat file entry ||6.850549805 +/- 0.3278271919 || 6.794470731 +/- 0.3027342241 || 6.677638317 +/- 0.3181179382 || 6.549555363 +/- 0.3026659672 || 6.384857074 +/- 0.3184246458 || 6.174846148 +/- 0.3010453307 || 6.092105322 +/- 0.2951787468 | ||.dat file entry ||6.850549805 +/- 0.3278271919 || 6.794470731 +/- 0.3027342241 || 6.677638317 +/- 0.3181179382 || 6.549555363 +/- 0.3026659672 || 6.384857074 +/- 0.3184246458 || 6.174846148 +/- 0.3010453307 || 6.092105322 +/- 0.2951787468 | ||
| Line 94: | Line 108: | ||
=Pure Se Analysis= | =Pure Se Analysis= | ||
| + | |||
| + | This will be using a new method as of 12/14 to find the error in the signal. To do this, find the intrinsic error by | ||
| + | |||
| + | <math> \frac{I_{Expanded}-I}{I} </math> | ||
| + | |||
| + | Where the expanded integral value is the integral from the stats box after the 2 channel window has been increased by 2 sigma. This number will then be multiplied by the background subtracted thin window signal. So the error in the signal is | ||
| + | |||
| + | <math> \sigma_I = I_{Expanded} - I </math> | ||
| + | |||
| + | ==First Pure Se Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 PureSe ThinWindow 400 640Sec.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 466700 \pm 49100 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 21120 \pm 103.16 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 445580 \pm 49100 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{445580}{240} \pm \frac{49100}{240} = 1856.58 \pm 204.58 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 240} \times 1856.58 \times 240 \times \lambda}{e^{\lambda \times 240}-1} = 1901.86 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 209.57 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 1901.86 \pm 209.57 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 3.06 +/- 0.30 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 1901.86 \times \frac{1}{0.9694} = 1961.89 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.0306 </math> | ||
| + | |||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the third measurement of the Pure Se sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1961.89 \pm 216.27 </math> | ||
| + | |||
| + | ==Second Pure Se Measurement== | ||
| + | |||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 PureSe 1100 1360Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 444100 \pm 43200 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 21120 \pm 102.82 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 422980 \pm 43200 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{422980}{260} \pm \frac{43200}{260} = 1626.85 \pm 166.15 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 260} \times 1626.85 \times 260 \times \lambda}{e^{\lambda \times 260}-1} = 1669.88 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 170.54 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 1669.88 \pm 170.54 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.31 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 1669.88 \times \frac{1}{0.9747} = 1713.22 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.025 </math> | ||
| + | |||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the third measurement of the Pure Se sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1713.22 \pm 175.05 </math> | ||
==Third Pure Se Measurement== | ==Third Pure Se Measurement== | ||
| Line 102: | Line 215: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 412800 \pm | + | <math> I \pm \sigma_I = 412800 \pm 39400 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 110: | Line 223: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 393808 \pm | + | <math> N \pm \sigma_N = 393808 \pm 39400 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{393808}{275} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{393808}{275} \pm \frac{39400}{275} = 1432.03 \pm 143.27 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 120: | Line 233: | ||
<math> A_{True} = \frac{e^{\lambda \times 275} \times 1432.03 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 1472.11 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 275} \times 1432.03 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 1472.11 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | |
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 147.28 Hz </math> | ||
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = 1472.11 \pm | + | <math> A_{True} \pm \sigma_{A_{True}} = 1472.11 \pm 147.28 Hz </math> |
Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3 | Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3 | ||
| Line 132: | Line 246: | ||
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> |
So the real activity for the third measurement of the Pure Se sample is | So the real activity for the third measurement of the Pure Se sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm 151.17 </math> |
Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion) | Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion) | ||
| Line 149: | Line 263: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 356800 \pm | + | <math> I \pm \sigma_I = 356800 \pm 34600 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 157: | Line 271: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 339004 \pm | + | <math> N \pm \sigma_N = 339004 \pm 34600 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{339004}{280} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{339004}{280} \pm \frac{34600}{280} = 1210.73 \pm 123.57 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 167: | Line 281: | ||
<math> A_{True} = \frac{e^{\lambda \times 280} \times 1210.73 \times 280 \times \lambda}{e^{\lambda \times 280}-1} =1245.24 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 280} \times 1210.73 \times 280 \times \lambda}{e^{\lambda \times 280}-1} =1245.24 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | |
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 127.09 Hz </math> | ||
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = 1245.24 \pm | + | <math> A_{True} \pm \sigma_{A_{True}} = 1245.24 \pm 127.09 Hz </math> |
Now we must correct for the dead time. The 4th run had an average count rate of 1274.32 Hz, which corr5esponds to a dead time of 2.26 +/- 0.33 | Now we must correct for the dead time. The 4th run had an average count rate of 1274.32 Hz, which corr5esponds to a dead time of 2.26 +/- 0.33 | ||
| Line 179: | Line 294: | ||
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.004 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.004 </math> | ||
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> |
So the real activity for the third measurement of the Pure Se sample is | So the real activity for the third measurement of the Pure Se sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1274.03 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1274.03 \pm 130.1 </math> |
==Fifth Pure Se Measurement== | ==Fifth Pure Se Measurement== | ||
| Line 195: | Line 310: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 304100 \pm | + | <math> I \pm \sigma_I = 304100 \pm 36100 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 203: | Line 318: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 285264 \pm | + | <math> N \pm \sigma_N = 285264 \pm 36100 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{285264}{290} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{285264}{290} \pm \frac{36100}{290} = 983.67 \pm 124.48 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 213: | Line 328: | ||
<math> A_{True} = \frac{e^{\lambda \times 290} \times 983.67 \times 290 \times \lambda}{e^{\lambda \times 290}-1} = 1012.72 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 290} \times 983.67 \times 290 \times \lambda}{e^{\lambda \times 290}-1} = 1012.72 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | |
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 128.16 Hz </math> | ||
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = 1012.72 \pm | + | <math> A_{True} \pm \sigma_{A_{True}} = 1012.72 \pm 128.16 Hz </math> |
Now we must correct for the dead time. The 5th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 2.26 +/- 0.33 | Now we must correct for the dead time. The 5th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 2.26 +/- 0.33 | ||
| Line 224: | Line 340: | ||
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| − | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | |
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | ||
So the real activity for the third measurement of the Pure Se sample is | So the real activity for the third measurement of the Pure Se sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1036.14 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1036.14 \pm 131.17 </math> |
==Sixth Pure Se Measurement== | ==Sixth Pure Se Measurement== | ||
| Line 240: | Line 355: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 258700 \pm | + | <math> I \pm \sigma_I = 258700 \pm 28100 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 248: | Line 363: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 243730 \pm | + | <math> N \pm \sigma_N = 243730 \pm 28100 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{243730}{280} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{243730}{280} \pm \frac{28100}{280} = 870.46 \pm 100.36 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 258: | Line 373: | ||
<math> A_{True} = \frac{e^{\lambda \times 280} \times 870.46 \times 280 \times \lambda}{e^{\lambda \times 280}-1} = 895.27 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 280} \times 870.46 \times 280 \times \lambda}{e^{\lambda \times 280}-1} = 895.27 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 103.22 Hz </math> |
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = 895.27 \pm | + | <math> A_{True} \pm \sigma_{A_{True}} = 895.27 \pm 103.22 Hz </math> |
Now we must correct for the dead time. The 6th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 1.96 +/- 0.26 | Now we must correct for the dead time. The 6th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 1.96 +/- 0.26 | ||
| Line 269: | Line 384: | ||
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| − | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | |
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | ||
So the real activity for the 6th measurement of the Pure Se sample is | So the real activity for the 6th measurement of the Pure Se sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 913.17 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 913.17 \pm 105.31 </math> |
== Seventh Pure Se Measurement== | == Seventh Pure Se Measurement== | ||
| Line 286: | Line 400: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 233500 \pm | + | <math> I \pm \sigma_I = 233500 \pm 24900 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 294: | Line 408: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 219178 \pm | + | <math> N \pm \sigma_N = 219178 \pm 24900 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{219178}{290} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{219178}{290} \pm \frac{24900}{290} = 755.79 \pm 85.86 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 304: | Line 418: | ||
<math> A_{True} = \frac{e^{\lambda \times 290} \times 755.79 \times 290 \times \lambda}{e^{\lambda \times 290}-1} = 778.11 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 290} \times 755.79 \times 290 \times \lambda}{e^{\lambda \times 290}-1} = 778.11 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | |
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 88.40 Hz </math> | ||
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = 778.11 \pm | + | <math> A_{True} \pm \sigma_{A_{True}} = 778.11 \pm 88.40 Hz </math> |
Now we must correct for the dead time. The 7th run had an average count rate of 1012 Hz, which corresponds to a dead time of 1.96 +/- 0.26 | Now we must correct for the dead time. The 7th run had an average count rate of 1012 Hz, which corresponds to a dead time of 1.96 +/- 0.26 | ||
| Line 315: | Line 430: | ||
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| − | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | |
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | ||
So the real activity for the 7th measurement of the Pure Se sample is | So the real activity for the 7th measurement of the Pure Se sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 793.67 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 793.67 \pm 90.19 </math> |
{| border="3" cellpadding="5" cellspacing="0" | {| border="3" cellpadding="5" cellspacing="0" | ||
|| || 400 <t< 640 sec || 1100 < t < 1360 sec || 1875 < t < 2150 || 2650 < t < 2930 sec || 3400 < t < 3690 sec || 4120 < t < 4400 sec || 4840 < t < 5130 sec | || || 400 <t< 640 sec || 1100 < t < 1360 sec || 1875 < t < 2150 || 2650 < t < 2930 sec || 3400 < t < 3690 sec || 4120 < t < 4400 sec || 4840 < t < 5130 sec | ||
|- | |- | ||
| − | ||.dat file entry ||7.58 +/- 0. | + | ||.dat file entry ||7.58 +/- 0.11 || 7.45 +/- 0.10 || 7.32 +/- 0.10 || 7.15 +/- 0.10 || 6.94 +/- 0.13 || 6.82 +/- 0.11 || 6.68 +/- 0.11 |
|- | |- | ||
|} | |} | ||
| + | Below is a table for the self comparison of the sample runs | ||
| + | |||
| + | {| border="3" cellpadding="5" cellspacing="0" | ||
| + | || || Run 1 || Run 2 || Run 3 || Run 4 || Run 5 || Run 6 || | ||
| + | |- | ||
| + | || Original Measurement (Hz) || 1961.89 +/- 216.27 || 1713.22 +/- 175.05 || 1510.32 +/- 151.17 || 1274.03 +/- 130.1 || 1036.14 +/- 131.17 || 913.17 +/- 105.31 | ||
| + | |- | ||
| + | ||n+1 Measurement (Hz) || 1713.22 +/- 175.05 || 1510.32 +/- 151.17 || 1274.03 +/- 130.1 || 1036.14 +/- 131.17 || 913.17 +/- 105.31 || 793.67 +/- 90.19 | ||
| + | |- | ||
| + | ||Time Correction Factor (Sec) ||720 || 790 || 780 || 760 || 710 ||730 | ||
| + | |- | ||
| + | ||n+1 Measurement Time Corrected (Hz) ||1980.97 +/- 202.41 || 1771.19 +/- 177.28 || 1491.08 +/- 152.26 || 1207.78 +/- 152.90 || 1053.76 +/- 121.52 || 919.56 +/- 104.50 | ||
| + | |- | ||
| + | ||n Measurement/n+1 Corrected Measurement || 0.99 +/- 0.15 || 0.97 +/- 0.14 || 1.01 +/- 0.14 || 1.05 +/- 0.17 || 0.98 +/- 0.17 || 0.99 +/- 0.16 | ||
| + | |- | ||
| + | |} | ||
=Se-Sage Mix Analysis= | =Se-Sage Mix Analysis= | ||
| Line 339: | Line 469: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = 342200 \pm | + | <math> I \pm \sigma_I = 342200 \pm 81400 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 347: | Line 477: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = 283320 \pm | + | <math> N \pm \sigma_N = 283320 \pm 81400 Counts</math> |
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{283320}{300} \pm \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{283320}{300} \pm \frac{84100}{300} = 944.4 \pm 280.33 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| Line 357: | Line 487: | ||
<math> A_{True} = \frac{e^{\lambda \times 300} \times 944.4 \times 300 \times \lambda}{e^{\lambda \times 300}-1} = 973.26 Hz </math> | <math> A_{True} = \frac{e^{\lambda \times 300} \times 944.4 \times 300 \times \lambda}{e^{\lambda \times 300}-1} = 973.26 Hz </math> | ||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 288.90 Hz </math> |
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = | + | <math> A_{True} \pm \sigma_{A_{True}} =973.26 \pm 288.90 Hz </math> |
Now we must correct for the dead time. The 1st run had an average count rate of 2434.44 Hz, which corresponds to a dead time of 5.06 +/- 0.39 | Now we must correct for the dead time. The 1st run had an average count rate of 2434.44 Hz, which corresponds to a dead time of 5.06 +/- 0.39 | ||
| Line 367: | Line 497: | ||
<math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 944.4 \times \frac{1}{0.9494} = 994.73 Hz </math> | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 944.4 \times \frac{1}{0.9494} = 994.73 Hz </math> | ||
| − | <math> \sigma_{ | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> |
| − | |||
| − | |||
So the real activity for the 1st measurement of the Mixed sample is | So the real activity for the 1st measurement of the Mixed sample is | ||
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 994.73 \pm | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 994.73 \pm 304.327 </math> |
| − | |||
==Activity of the Second Measurement== | ==Activity of the Second Measurement== | ||
| Line 384: | Line 511: | ||
From this we can see that | From this we can see that | ||
| − | <math> I \pm \sigma_I = | + | <math> I \pm \sigma_I = 300100 \pm 57700 Counts </math> |
and the integrated background is given by | and the integrated background is given by | ||
| Line 392: | Line 519: | ||
Now we can find the background subtracted signal | Now we can find the background subtracted signal | ||
| − | <math> N \pm \sigma_N = | + | <math> N \pm \sigma_N = 258940 \pm 57700 Counts</math> |
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{258940}{290} \pm \frac{57700}{290} = 892.90 \pm 198.97 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 290} \times 892.90 \times 290 \times \lambda}{e^{\lambda \times 300}-1} = 919.27 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 204.84 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 919.27 \pm 204.84 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The 1st run had an average count rate of 1756.30 Hz, which corresponds to a dead time of 3.06 +/- 0.30 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 919.27 \times \frac{1}{0.9694} = 948.29 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.0.003 </math> | ||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 948.20 \pm 211.33 </math> | ||
| + | |||
| + | ==Activity of the Third Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 MixSpec 1480 1775Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 267200 \pm 45600 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 32840 \pm 131.04 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 234360 \pm 45600 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{234360}{295} \pm \frac{45600}{295} = 794.44 \pm 154.58 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 295} \times 794.44 \times 295 \times \lambda}{e^{\lambda \times 295}-1} = 818.31 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 159.22 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 818.31 \pm 159.22 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The 1st run had an average count rate of 1401.98 Hz, which corresponds to a dead time of 2.53 +/- 0.31 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 818.31 \times \frac{1}{0.9747} = 839.55 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 839.55 \pm 163.38 </math> | ||
| + | |||
| + | ==Fourth Mix Sample Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 MixSpec 2250 2550Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 238600 \pm 39100 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 28920 \pm 116.94 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 209680 \pm 39100 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{209680}{300} \pm \frac{39100}{300} = 698.93 \pm 130.33 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 300} \times 698.93 \times 300 \times \lambda}{e^{\lambda \times 300}-1} = 720.29 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 134.31 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 720.29 \pm 134.31 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The 1st run had an average count rate of 1401.98 Hz, which corresponds to a dead time of 2.53 +/- 0.31 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 720.29 \times \frac{1}{0.9747} = 738.99 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| + | |||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math>> | ||
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 738.99 \pm 137.82 </math> | ||
| + | |||
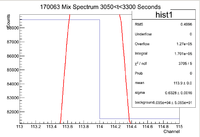
| + | ==Activity of the Fifth Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 MixSpec 3050 3300Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 170100 \pm 28500 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 21900 \pm 101.3 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 148200 \pm 28500 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{148200}{250} \pm \frac{28500}{250} = 592.8 \pm 114 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 250} \times 592.8 \times 250 \times \lambda}{e^{\lambda \times 250}-1} = 607.87 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 116.90 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 607.87 \pm 116.90 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The 1st run had an average count rate of 1025.13 Hz, which corresponds to a dead time of 1.92 +/- 0.26 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 607.8 \times \frac{1}{0.9808} = 619.70 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 </math> | ||
| + | |||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 619.70 \pm 119.2 </math> | ||
| + | |||
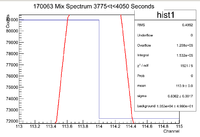
| + | ==Sixth Mix Sample Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 MixSpec 3775 4050Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 153200 \pm 28000 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 21060 \pm 99.8 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 132140 \pm 28000 Counts</math> | ||
Now convert this into an activity by dividing by the runtime | Now convert this into an activity by dividing by the runtime | ||
| − | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{ | + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{132140}{275} \pm \frac{28000}{275} = 480.51 \pm 101.81 Hz </math> |
Now we can find the true value using the integrated measurement | Now we can find the true value using the integrated measurement | ||
| − | <math> A_{True} = \frac{e^{\lambda \times | + | <math> A_{True} = \frac{e^{\lambda \times 275} \times 480.51 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 493.96 Hz </math> |
| + | |||
| − | <math> \sigma_{A_{True}} = \frac{e^{\lambda \times | + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 104.66 Hz </math> |
So now the true value for the activity is | So now the true value for the activity is | ||
| − | <math> A_{True} \pm \sigma_{A_{True}} = | + | <math> A_{True} \pm \sigma_{A_{True}} = 493.96 \pm 104.66 Hz </math> |
| − | Now we must correct for the dead time. The 1st run had an average count rate of | + | Now we must correct for the dead time. The 1st run had an average count rate of 898.19 Hz, which corresponds to a dead time of 1.65 +/- 0.34 |
| − | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = | + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 493.96 \times \frac{1}{0.9835} = 502.25 Hz </math> |
<math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.004 </math> | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.004 </math> | ||
| − | <math> \sigma_{A_{True}^{DT}} = \sqrt{ | + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> |
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 502.25 \pm 106.43 </math> | ||
| + | |||
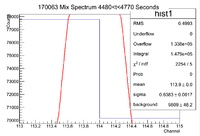
| + | ==Activity of the 7th Measurement== | ||
| + | |||
| + | Below is the histogram of interest | ||
| + | |||
| + | [[File:170063 MixSpec 4480 4770Sec ThinWindow.png|200px]] | ||
| + | |||
| + | From this we can see that | ||
| + | |||
| + | <math> I \pm \sigma_I = 147900 \pm 26400 Counts </math> | ||
| + | |||
| + | and the integrated background is given by | ||
| + | |||
| + | <math> B \pm \sigma_B = 19618 \pm 96.4 Counts</math> | ||
| + | |||
| + | Now we can find the background subtracted signal | ||
| + | |||
| + | <math> N \pm \sigma_N = 128282 \pm 26400 Counts</math> | ||
| + | |||
| + | Now convert this into an activity by dividing by the runtime | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{128282}{290} \pm \frac{26400}{290} = 442.35 \pm 91.03 Hz </math> | ||
| + | |||
| + | Now we can find the true value using the integrated measurement | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 290} \times 442.35 \times 290 \times \lambda}{e^{\lambda \times 290}-1} = 455.41 Hz </math> | ||
| + | |||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + (\frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2})^2 \times \sigma_{\lambda}^2} = 93.72 Hz </math> | ||
| + | |||
| + | So now the true value for the activity is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A_{True}} = 455.41 \pm 93.72 Hz </math> | ||
| + | |||
| + | Now we must correct for the dead time. The 1st run had an average count rate of 846.40 Hz, which corresponds to a dead time of 1.65 +/- 0.34 | ||
| + | |||
| + | <math> A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 455.41 \times \frac{1}{0.9835} = 463.05 Hz </math> | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{1-DT^2} = 0.004 </math> <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the real activity for the 2nd measurement of the Mixed sample is | ||
| + | |||
| + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 463.05 \pm 95.31 </math> | ||
| + | |||
| + | {| border="3" cellpadding="5" cellspacing="0" | ||
| + | || || 0<t<300 || 730 <t< 1020 || 1480<t<1775 || 2250<t<2550 || 3050<t<3300 || 3775<t<4050 || 4480<t<4770 | ||
| + | |- | ||
| + | ||Data File Entry || 6.90 +/- 0.30 || 6.85 +/- 0.22 ||6.73 +/- 0.19 || 6.61 +/- 0.19 || 6.43 +/- 0.19 || 6.23 +/- 0.21 || 6.14 +/- 0.21 | ||
| + | |- | ||
| + | |} | ||
| − | |||
| − | + | Below is a table to check the activities against later measurements by tracing the activity back in time and taking a ratio | |
{| border="3" cellpadding="5" cellspacing="0" | {| border="3" cellpadding="5" cellspacing="0" | ||
| − | || || | + | || || Run 1 || Run 2 || Run 3 || Run 4 || Run 5 || Run 6 |
| + | |- | ||
| + | || Original Measurement (Hz) || 994.73 +/- 304.327 || 948.20 +/- 211.33 || 839.55 +/- 163.38 || 738.99 +/- 137.82 || 619.70 +/- 119.20 || 502.25 +/- 106.43 | ||
|- | |- | ||
| − | || | + | ||n+1 Measurement (Hz) || 948.20 +/- 211.33 || 839.55 +/- 163.38 ||738.99 +/- 137.82 || 619.70 +/- 119.20 ||502.25 +/- 106.43 || 463.05 +/- 95.31 |
| + | |- | ||
| + | ||Time Correction Factor (Sec) ||720 || 755 || 775 || 750 || 750 || 720 | ||
| + | |- | ||
| + | ||n+1 Measurement Time Corrected (Hz) ||1096.39 +/- 244.36 || 977.63 +/- 190.25 || 864.01 +/- 161.14 || 720.90 +/- 138.67 || 584.27 +/- 123.81 || 535.42 +/- 110.21 | ||
| + | |- | ||
| + | ||n Measurement/n+1 Corrected Measurement || 0.91 +/- 0.33 || 0.97 +/- 0.29 || 0.97 +/- 0.26|| 1.02 +/- 0.27 || 1.06 +/- 0.3 || 0.94 +/- 0.28 | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | ==Plots== | ||
| + | |||
| + | Below is a table for the plots of the cross sample ratios | ||
| + | |||
| + | {| border="3" cellpadding="5" cellspacing="0" | ||
| + | || || Run 1 || Run 2 || Run 3 || Run 4 || Run 5 || Run 6 || Run 7 | ||
| + | |- | ||
| + | || Mix Measurement (Hz) || 994.73 +/- 304.327 || 948.20 +/- 211.33 || 839.55 +/- 163.38 || 738.99 +/- 137.82 || 619.70 +/- 119.2 || 502.25 +/- 106.43 || 463.05 +/- 95.31 | ||
| + | |- | ||
| + | ||Original Pure Se Measurement (Hz) || 1961.89 +/- 216.27 || 1713.22 +/- 175.05 || 1510.32 +/- 151.17 || 1274.03 +/- 130.1 || 1036.14 +/- 131.17 || 913.17 +/- 105.31 || 793.67 +/- 90.19 | ||
| + | |- | ||
| + | ||Time Correction Factor (Sec) ||340 || 340 ||375 || 380 || 390 || 350 || 360 | ||
| + | |- | ||
| + | ||Time Corrected Mix Measurement (Hz) ||1065.33 +/- 325.93 || 1015.50 +/- 226.33 || 905.51 +/- 176.22 || 797.85 +/- 148.80 || 670.41 +/- 128.95 || 538.98 +/- 114.214 || 497.92 +/- 102.49 | ||
| + | |- | ||
| + | || Time Corrected Mix Measurement/Pure Se Measurement || 0.54 +/- 0.18 || 0.59 +/- 0.14 || 0.60 +/- 0.13 || 0.63 +/- 0.13 || 0.65 +/- 0.15 || 0.59 +/- 0.14 || 0.63 +/- 0.15 | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Below are the time vs. frequency plots | ||
| + | |||
| + | [[File:170063 MixHLPlot 1 11 18.png|200px]] | ||
| + | [[File:170063 PureSeHLPlot 1 11 18.png|200px]] | ||
| + | |||
| + | By exponentiating we find that the initial activity of the Mixture is 1056.48 +/- 2.91 Hz, while the pure sample has an initial activity of 2162.90 +/- 5.16 Hz which gives a ratio of | ||
| + | |||
| + | <math> 0.488 \pm 0.002 </math> | ||
| + | |||
| + | To check consistency I would time correct measurements and take a ratio to compare, for example measurement 1 was taken and a 2nd measurement was taken some time later. So correct the rate of the second measurement back to the first measurement by using the radioactive decay equation, then take a ratio of these 2 numbers. | ||
| + | |||
| + | [[File:170063 Mix RateRatios 1 11 18.png|200px]] | ||
| + | [[File:170063 PureSe RateRatio 1 11 18.png|200px]] | ||
| + | |||
| + | Another check to do is to take the ratio of the mixture and the pure selenium sample (time corrected to the same time for each measurement) and see if the ratio here is relatively constant | ||
| + | |||
| + | [[File:170063 CrossSample RateRatios 1 11 18.png|200px]] | ||
| + | |||
| + | By exponentiating we find that the initial activity of the Mixture is 1082.15 +/- 174.89 Hz, while the pure sample has an initial activity of 2169.13 +/- 175.01 Hz which gives a ratio of | ||
| + | |||
| + | Thin Window Mean + 2 Sigma:<math> 0.50 \pm 0.09 </math> ,Original Window + 2 Sigma or original window | ||
| + | |||
| + | We can also check the ratio of the nickel with the selenium mixture. The rate of the nickel foil was <math> 1.127931 \times 10^6 \pm 7.258 \times 10^3 Hz </math> | ||
| + | |||
| + | So using the efficiency corrected rate for the soil, we find that the ratio is | ||
| + | |||
| + | <math> 0.134 \pm 0.001 </math> | ||
| + | |||
| + | |||
| + | The measurement was made 20cm away from the detector face, which has an efficiency of 0.70 +/- 0.0011, so the measurements with the efficiency taken into account are | ||
| + | |||
| + | 150925.7143 +/- 392.5923 Hz for the mixture and | ||
| + | |||
| + | 308985.7143 +/- 882.6876 Hz for the pure selenium sample | ||
Latest revision as of 19:19, 11 January 2018
In order to try to pin down the ratio of pure selenium to the selenium in the soil, try using a 2 channel window to find the signal. The uncertainty in the number of counts in the signal will be determined by subtracting the counts from the 2 channel window from the counts from a window expanded by 1 standard deviation, then divided by the original number of counts in the 2 channel window. Since the max value is fixed, it does not appear in the stats box, but I have included it in the table. It would seem that widening the gaussian function by half of its standard deviation yields results that agree up to 3 digits after the decimal with the result of widening the gaussian by its standard deviation. This would imply not much has changed between these methods.
Changes Made to table:
12/14: Error in signal changed to (try to not underestimate error) This includes changing the expanded window to a window expanded off of the 2 channel window
Below is the table for the Se-Ash Mixture
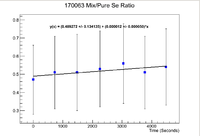
Below is a plot of the ratio of the activities where the pure selenium sample has been time corrected back to match the run time of the mixture.
Note that this does give the expected result that the ratio between the two samples is statistically the same as 0.5, which is the ratio of the masses. The only problem here is that the error is quite large, The average of the uncertainty divided by the mean is 39.6%.
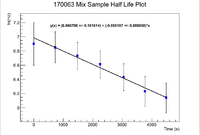
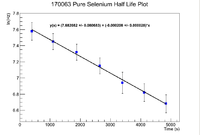
Below are the half life plots for the Pure Selenium sample and the ash mixture
The slope of the mixture plot gives a half life of 63.48 +/- 26.85 minutes. This does overlap, but the error is extremely large.
The slope of the pure selenium sample plot gives a half life of 56.08 +/- 16.33 minutes. Again this does overlap, but the error is still quite large.
The ratio of the initial activities is 0.49 +/- 0.13. Now this does fall within 1 standard deviation of 0.5, which is the value we want.
Dead Time Corrected
I have shown that by tracing the activity back in time for the pure selenium sample that the activities are the same here LB Thesis Thin Window Analysis, but now I must make sure that this will actually give the ratio that is expected.
Begin with the third measurement that was taken for the pure selenium sample
Pure Se Analysis
This will be using a new method as of 12/14 to find the error in the signal. To do this, find the intrinsic error by
Where the expanded integral value is the integral from the stats box after the 2 channel window has been increased by 2 sigma. This number will then be multiplied by the background subtracted thin window signal. So the error in the signal is
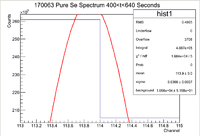
First Pure Se Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 3.06 +/- 0.30
So the real activity for the third measurement of the Pure Se sample is
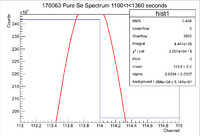
Second Pure Se Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.31
So the real activity for the third measurement of the Pure Se sample is
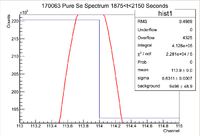
Third Pure Se Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3
So the real activity for the third measurement of the Pure Se sample is
Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion)
Fourth Pure Se Measurement
Now do the analysis for the 4th measurement taken on the pure selenium sample.
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 4th run had an average count rate of 1274.32 Hz, which corr5esponds to a dead time of 2.26 +/- 0.33
So the real activity for the third measurement of the Pure Se sample is
Fifth Pure Se Measurement
Now do the analysis for the 5th measurement taken on the pure selenium sample.
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 5th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 2.26 +/- 0.33
So the real activity for the third measurement of the Pure Se sample is
Sixth Pure Se Measurement
Now do the analysis for the 6th measurement taken on the pure selenium sample.
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 6th run had an average count rate of 1168.06 Hz, which corresponds to a dead time of 1.96 +/- 0.26
So the real activity for the 6th measurement of the Pure Se sample is
Seventh Pure Se Measurement
Now do the analysis for the 7th measurement taken on the pure selenium sample.
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 7th run had an average count rate of 1012 Hz, which corresponds to a dead time of 1.96 +/- 0.26
So the real activity for the 7th measurement of the Pure Se sample is
| 400 <t< 640 sec | 1100 < t < 1360 sec | 1875 < t < 2150 | 2650 < t < 2930 sec | 3400 < t < 3690 sec | 4120 < t < 4400 sec | 4840 < t < 5130 sec | |
| .dat file entry | 7.58 +/- 0.11 | 7.45 +/- 0.10 | 7.32 +/- 0.10 | 7.15 +/- 0.10 | 6.94 +/- 0.13 | 6.82 +/- 0.11 | 6.68 +/- 0.11 |
Below is a table for the self comparison of the sample runs
| Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | ||
| Original Measurement (Hz) | 1961.89 +/- 216.27 | 1713.22 +/- 175.05 | 1510.32 +/- 151.17 | 1274.03 +/- 130.1 | 1036.14 +/- 131.17 | 913.17 +/- 105.31 | |
| n+1 Measurement (Hz) | 1713.22 +/- 175.05 | 1510.32 +/- 151.17 | 1274.03 +/- 130.1 | 1036.14 +/- 131.17 | 913.17 +/- 105.31 | 793.67 +/- 90.19 | |
| Time Correction Factor (Sec) | 720 | 790 | 780 | 760 | 710 | 730 | |
| n+1 Measurement Time Corrected (Hz) | 1980.97 +/- 202.41 | 1771.19 +/- 177.28 | 1491.08 +/- 152.26 | 1207.78 +/- 152.90 | 1053.76 +/- 121.52 | 919.56 +/- 104.50 | |
| n Measurement/n+1 Corrected Measurement | 0.99 +/- 0.15 | 0.97 +/- 0.14 | 1.01 +/- 0.14 | 1.05 +/- 0.17 | 0.98 +/- 0.17 | 0.99 +/- 0.16 |
Se-Sage Mix Analysis
Activity of the First Measurement
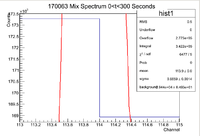
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 2434.44 Hz, which corresponds to a dead time of 5.06 +/- 0.39
So the real activity for the 1st measurement of the Mixed sample is
Activity of the Second Measurement
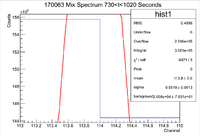
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 1756.30 Hz, which corresponds to a dead time of 3.06 +/- 0.30
So the real activity for the 2nd measurement of the Mixed sample is
Activity of the Third Measurement
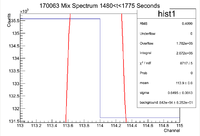
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 1401.98 Hz, which corresponds to a dead time of 2.53 +/- 0.31
So the real activity for the 2nd measurement of the Mixed sample is
Fourth Mix Sample Measurement
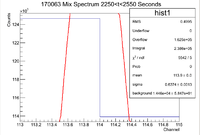
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 1401.98 Hz, which corresponds to a dead time of 2.53 +/- 0.31
>
So the real activity for the 2nd measurement of the Mixed sample is
Activity of the Fifth Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 1025.13 Hz, which corresponds to a dead time of 1.92 +/- 0.26
So the real activity for the 2nd measurement of the Mixed sample is
Sixth Mix Sample Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 898.19 Hz, which corresponds to a dead time of 1.65 +/- 0.34
So the real activity for the 2nd measurement of the Mixed sample is
Activity of the 7th Measurement
Below is the histogram of interest
From this we can see that
and the integrated background is given by
Now we can find the background subtracted signal
Now convert this into an activity by dividing by the runtime
Now we can find the true value using the integrated measurement
So now the true value for the activity is
Now we must correct for the dead time. The 1st run had an average count rate of 846.40 Hz, which corresponds to a dead time of 1.65 +/- 0.34
So the real activity for the 2nd measurement of the Mixed sample is
| 0<t<300 | 730 <t< 1020 | 1480<t<1775 | 2250<t<2550 | 3050<t<3300 | 3775<t<4050 | 4480<t<4770 | |
| Data File Entry | 6.90 +/- 0.30 | 6.85 +/- 0.22 | 6.73 +/- 0.19 | 6.61 +/- 0.19 | 6.43 +/- 0.19 | 6.23 +/- 0.21 | 6.14 +/- 0.21 |
Below is a table to check the activities against later measurements by tracing the activity back in time and taking a ratio
| Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | |
| Original Measurement (Hz) | 994.73 +/- 304.327 | 948.20 +/- 211.33 | 839.55 +/- 163.38 | 738.99 +/- 137.82 | 619.70 +/- 119.20 | 502.25 +/- 106.43 |
| n+1 Measurement (Hz) | 948.20 +/- 211.33 | 839.55 +/- 163.38 | 738.99 +/- 137.82 | 619.70 +/- 119.20 | 502.25 +/- 106.43 | 463.05 +/- 95.31 |
| Time Correction Factor (Sec) | 720 | 755 | 775 | 750 | 750 | 720 |
| n+1 Measurement Time Corrected (Hz) | 1096.39 +/- 244.36 | 977.63 +/- 190.25 | 864.01 +/- 161.14 | 720.90 +/- 138.67 | 584.27 +/- 123.81 | 535.42 +/- 110.21 |
| n Measurement/n+1 Corrected Measurement | 0.91 +/- 0.33 | 0.97 +/- 0.29 | 0.97 +/- 0.26 | 1.02 +/- 0.27 | 1.06 +/- 0.3 | 0.94 +/- 0.28 |
Plots
Below is a table for the plots of the cross sample ratios
| Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | Run 7 | |
| Mix Measurement (Hz) | 994.73 +/- 304.327 | 948.20 +/- 211.33 | 839.55 +/- 163.38 | 738.99 +/- 137.82 | 619.70 +/- 119.2 | 502.25 +/- 106.43 | 463.05 +/- 95.31 |
| Original Pure Se Measurement (Hz) | 1961.89 +/- 216.27 | 1713.22 +/- 175.05 | 1510.32 +/- 151.17 | 1274.03 +/- 130.1 | 1036.14 +/- 131.17 | 913.17 +/- 105.31 | 793.67 +/- 90.19 |
| Time Correction Factor (Sec) | 340 | 340 | 375 | 380 | 390 | 350 | 360 |
| Time Corrected Mix Measurement (Hz) | 1065.33 +/- 325.93 | 1015.50 +/- 226.33 | 905.51 +/- 176.22 | 797.85 +/- 148.80 | 670.41 +/- 128.95 | 538.98 +/- 114.214 | 497.92 +/- 102.49 |
| Time Corrected Mix Measurement/Pure Se Measurement | 0.54 +/- 0.18 | 0.59 +/- 0.14 | 0.60 +/- 0.13 | 0.63 +/- 0.13 | 0.65 +/- 0.15 | 0.59 +/- 0.14 | 0.63 +/- 0.15 |
Below are the time vs. frequency plots
By exponentiating we find that the initial activity of the Mixture is 1056.48 +/- 2.91 Hz, while the pure sample has an initial activity of 2162.90 +/- 5.16 Hz which gives a ratio of
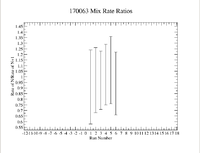
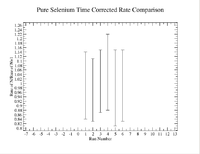
To check consistency I would time correct measurements and take a ratio to compare, for example measurement 1 was taken and a 2nd measurement was taken some time later. So correct the rate of the second measurement back to the first measurement by using the radioactive decay equation, then take a ratio of these 2 numbers.
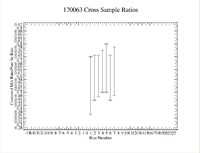
Another check to do is to take the ratio of the mixture and the pure selenium sample (time corrected to the same time for each measurement) and see if the ratio here is relatively constant
By exponentiating we find that the initial activity of the Mixture is 1082.15 +/- 174.89 Hz, while the pure sample has an initial activity of 2169.13 +/- 175.01 Hz which gives a ratio of
Thin Window Mean + 2 Sigma: ,Original Window + 2 Sigma or original window
We can also check the ratio of the nickel with the selenium mixture. The rate of the nickel foil was
So using the efficiency corrected rate for the soil, we find that the ratio is
The measurement was made 20cm away from the detector face, which has an efficiency of 0.70 +/- 0.0011, so the measurements with the efficiency taken into account are
150925.7143 +/- 392.5923 Hz for the mixture and
308985.7143 +/- 882.6876 Hz for the pure selenium sample