|
|
| Line 133: |
Line 133: |
| | So the real activity for the third measurement of the Pure Se sample is | | So the real activity for the third measurement of the Pure Se sample is |
| | | | |
| − | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1472.11 \pm 5.08 </math> | + | <math> A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm 5.08 </math> |
| | | | |
| | Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion) | | Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion) |
In order to try to pin down the ratio of pure selenium to the selenium in the soil, try using a 2 channel window to find the signal. The error in the signal will be found by integrating the fit gaussian function over the window and "widening" it by half its standard deviation. Since the max value is fixed, it does not appear in the stats box, but I have included it in the table. It would seem that widening the gaussian function by half of its standard deviation yields results that agree up to 3 digits after the decimal with the result of widening the gaussian by its standard deviation. This would imply not much has changed between these methods.
|
400 <t< 640 sec |
1100 < t < 1360 sec |
1875 < t < 2150 |
2650 < t < 2930 sec |
3400 < t < 3690 sec |
4120 < t < 4400 sec |
4840 < t < 5130 sec
|
| Thin Window |
 |
 |
 |
 |
 |
 |

|
| Original Window |
 |
 |
 |
 |
 |
 |

|
| Expanded Window |
 |
 |
 |
 |
 |
 |

|
| Maximum of Histogram |
260980 |
241756 |
220348 |
191476 |
165549 |
139528 |
130930
|
| Original Background |
10560 +/- 51.58 |
10560 +/- 51.41 |
9496 +/- 48.9 |
8898 +/- 47.1 |
9418 +/- 48.2 |
7485 +/- 43 |
7032 +/- 31.1
|
| Expanded Background |
10750 +/- 42.42 |
10630 +/- 42.09 |
9674 +/- 40.2 |
9029 +/- 38.7 |
9248 +/- 39.1 |
7634 +/- 35.5 |
7161 +/- 34.2
|
| Signal Background (Take Larger Error) |
10560 +/- 51.58 |
10560 +/- 51.41 |
9496 +/- 48.9 |
8898 +/- 47.1 |
9418 +/- 48.2 |
7485 +/- 43 |
7161 +/- 34.2
|
| Integrated Background |
21120 +/- 103.16 |
21120 +/- 102.82 |
18992 +/- 97.8 |
17796 +/- 94.2 |
18836 +/- 96.4 |
14970 +/- 86 |
14322 +/- 68.4
|
| Signal in Thin Window |
466700 +/- 100640 |
444100 +/- 107283 |
412800 +/- 105315 |
356800 +/- 90071 |
304100 +/- 70533 |
258700 +/- 63093 |
233500 +/- 52318
|
| Background Subtracted Signal |
445580 +/- 100640 |
422980 +/- 107283 |
393808 +/- 105315 |
339004 +/- 90071 |
285264 +/- 70533 |
243730 +/- 63093 |
219178 +/- 52318
|
| Time Correction Factor (Sec) |
400 |
370 |
395 |
400 |
350 |
345 |
360
|
| Corrected Counts |
483015.53 +/- 109095.5248 |
455750 +/- 115595.0622 |
426463.63 +/- 114048.1804 |
367485.52 +/- 97638.49218 |
306127.92 +/- 75691.81615 |
261292.55 +/- 67639.40782 |
235683.31 +/- 56257.91145
|
|
|
| .dat file entry |
7.607165162 +/- 0.2258633895 |
7.469018062 +/- 0.2536369988 |
7.346511269 +/- 0.2676838585 |
7.179649592 +/- 0.2656934406 |
6.96187741 +/- 0.2472555138 |
6.838606337 +/- 0.2588646627 |
6.700363353 +/- 0.2387012956
|
Below is the table for the Se-Ash Mixture
|
0 <t< 300 sec |
730 < t < 1020 sec |
1480 < t < 1775 |
2250 < t < 2550 sec |
3050< t < 3300 sec |
3775 < t < 4050 sec |
4480 < t < 4770 sec
|
| Thin Window |
 |
 |
 |
 |
 |
 |

|
| Original Window |
 |
 |
 |
 |
 |
 |

|
| Expanded Window |
 |
 |
 |
 |
 |
 |

|
| Maximum of Histogram |
173289 |
155770 |
135740 |
124656 |
88582 |
80993 |
77781
|
| Original Background |
29440 +/- 84.93 |
20580 +/- 70.31 |
16420 +/- 62.52 |
14460 +/- 58.47 |
10950 +/- 50.65 |
10530 +/- 49.90 |
9809 +/- 48.2
|
| Expanded Background |
28960 +/- 69.12 |
20580 +/- 57.79 |
16500 +/- 51.60 |
14500 +/- 48.2 |
10630 +/- 41.29 |
10460 +/- 41.01 |
9814 +/- 39.7
|
| Signal Background (Take Larger Error) |
29440 +/- 84.93 |
20580 +/- 70.31 |
16420 +/- 62.52 |
14460 +/- 58.47 |
10950 +/- 50.65 |
10530 +/- 49.90 |
9809 +/- 48.2
|
| Integrated Background |
58880 +/- 169.86 |
41160 +/- 140.62 |
32840 +/- 131.04 |
28920 +/- 116.94 |
21900 +/- 101.3 |
21060 +/- 99.8 |
19618 +/- 96.4
|
| Signal in Thin Window |
342200 +/- 92880 |
300100 +/- 78390 |
267200 +/- 74626 |
238600 +/- 63463 |
170100 +/- 46436 |
153200 +/- 39780 |
147900 +/- 38766
|
| Background Subtracted Signal |
283320 +/- 92880 |
258940 +/- 78390 |
234360 +/- 74626 |
209680 +/- 63463 |
148200 +/- 46436.11 |
132140 +/- 39780.13 |
128282 +/- 37866.12
|
| .dat file entry |
6.850549805 +/- 0.3278271919 |
6.794470731 +/- 0.3027342241 |
6.677638317 +/- 0.3181179382 |
6.549555363 +/- 0.3026659672 |
6.384857074 +/- 0.3184246458 |
6.174846148 +/- 0.3010453307 |
6.092105322 +/- 0.2951787468
|
Below is a plot of the ratio of the activities where the pure selenium sample has been time corrected back to match the run time of the mixture.
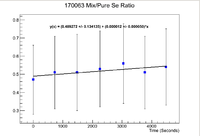
Note that this does give the expected result that the ratio between the two samples is statistically the same as 0.5, which is the ratio of the masses. The only problem here is that the error is quite large, The average of the uncertainty divided by the mean is 39.6%.
Below are the half life plots for the Pure Selenium sample and the ash mixture


The slope of the mixture plot gives a half life of 63.48 +/- 26.85 minutes. This does overlap, but the error is extremely large.
The slope of the pure selenium sample plot gives a half life of 56.08 +/- 16.33 minutes. Again this does overlap, but the error is still quite large.
The ratio of the initial activities is 0.49 +/- 0.13. Now this does fall within 1 standard deviation of 0.5, which is the value we want.
Dead Time Corrected
I have shown that by tracing the activity back in time for the pure selenium sample that the activities are the same here LB Thesis Thin Window Analysis, but now I must make sure that this will actually give the ratio that is expected.
Begin with the third measurement that was taken for the pure selenium sample
Below is the histogram of interest
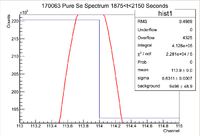
From this we can see that
[math] I \pm \sigma_I = 412800 \pm 642.50 Counts [/math]
and the integrated background is given by
[math] B \pm \sigma_B = 18992 \pm 97.8 Counts[/math]
Now we can find the background subtracted signal
[math] N \pm \sigma_N = 393808 \pm 649.90 Counts[/math]
Now convert this into an activity by dividing by the runtime
[math] A_{Measure} \pm \sigma_{A_{Measure}} = \frac{393808}{275} \pm \frac{649.90}{275} = 1432.03 \pm 2.36 Hz [/math]
Now we can find the true value using the integrated measurement
[math] A_{True} \pm \sigma_{A_{True}} = \frac{e^{\lambda \times 275} \times 1432.03 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 1472.11 Hz [/math]
[math] \sigma_{A_{True}} = \frac{e^{\lambda \times 275} \times 2.36 \times 275 \times \lambda}{e^{\lambda \times 275}-1} = 2.43 Hz [/math]
So now the true value for the activity is
[math] A_{True} \pm \sigma_{A_{True}} = 1472.11 \pm 2.43 Hz [/math]
Now we must correct for the dead time. The third run had an average count rate of 1387.06 Hz, which corresponds to a dead time of 2.53 +/- 0.3
[math] A_{True}^{DT} = A_{True} \times \frac{1}{1-DT} = 1472.11 \times \frac{1}{0.9747} = 1510.32 Hz [/math]
[math] \sigma_{DTC}} = \frac{\sigma_{DT}}{1-DT^2} = 0.003 [/math]
[math] \sigma_{A_{True}^{DT} = \sqrt{DTC^2 \times \sigma_{A}^2 + A^2 \times \sigma_{DTC}^2} = \sqrt{1.03^2 \times 2.43^2 + 1472.11^2 \times 0.003^2} = 5.08 Hz [/math]
So the real activity for the third measurement of the Pure Se sample is
[math] A_{True}^{DT} \pm \sigma_{A_{True}^{DT}} = 1510.32 \pm 5.08 [/math]
Below is a table representing the numbers that will be put into a data file to be linearly fit (Also using the values from the thesis portion)
|
400 <t< 640 sec |
1100 < t < 1360 sec |
1875 < t < 2150 |
2650 < t < 2930 sec |
3400 < t < 3690 sec |
4120 < t < 4400 sec |
4840 < t < 5130 sec
|
| .dat file entry |
7.58 +/- 0.003 |
7.45 +/- 0.003 |
|













































