Scattering Cross Section
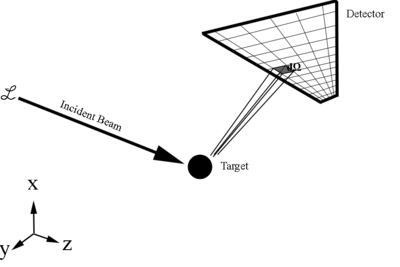
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section[/math]
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Transforming Cross Section Between Frames
Cross Section as a Function of p, θ, Φ
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
[math]\sigma=\frac{N}{\mathcal L}=constant\ number[/math]
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations.
[math]\therefore\ \sigma_{CM}=\sigma_{Lab}[/math]
This implies that the number of particles going into the solid-angle element d ΩLab and having a momentum between pLab and pLab+dpLabbe the same as the number going into the corresponding solid-angle element dΩCM and having a corresponding momentum between pCM and pCM+dpCM
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega}dp \,d\Omega=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^* \,\partial \Omega^* }dp^* \, d\Omega^*[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
Expressing this in terms of the solid angle components,
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega}\partial p \,\sin{\theta} \,d\theta \,d\phi=\frac{d^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{dp^* \, d\Omega^*}dp^*\, \sin{\theta^*}\,d\theta^* \,d\phi^*[/math]
As shown earlier,
[math]\phi=\phi^*[/math]
Thus,
[math]\Rightarrow\ d\phi=d\phi^*[/math]
Simplify our expression for the cross section gives:
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p \,\partial \Omega} dp \,\sin{\theta}\,d\theta=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*}dp^*\, \sin{\theta^*}\,d\theta^*[/math]
We can use the fact that
[math]\sin{\theta}\ d\theta=d(\cos{\theta})[/math]
To give
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} dp\,d(\cos{\theta})=\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*}dp^*\, d(\cos{\theta^*})[/math]
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{dp^*\,d(\cos{\theta^*})}{dp\,d(\cos{\theta})}[/math]
[math]\frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{\partial (p^*\,\cos{\theta^*)}}{\partial (p\,\cos{\theta})}[/math]
Using Chain Rule
We can use the chain rule to find the transformation term on the right hand side:
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p^*\, \theta^*\, \phi^*)} \frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)} \frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)} \frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)} \frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{\partial (p^*\, \cos{\theta^*})}{\partial (p\, \cos{\theta})}[/math]
Starting with the term:
[math]\frac{\partial (p^*\, \cos{\theta^*})} {\partial (p^*\, \theta^*\phi^*)}=\frac{d p^*\, \sin{\theta^*} \, d \theta^* \, d \phi^*}{d p^*\, d \theta^*\, d \phi^*}=\sin{\theta^*}[/math]
Similarly,
[math]\frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{1}{\sin{\theta}}[/math]
Using the conversion of cartesian to spherical coordinates we know:
[math]\begin{cases}
p_x=p\, \sin{\theta}\, \cos{\phi} \\
p_y=p\, \sin{\theta}\, \sin{\phi} \\
p_z=p\, \cos{\theta}
\end{cases}[/math]
and the fact that as was shown earlier, that
[math]\begin{cases}
p^*_x=p_x \\
p^*_y=p_y \\
\phi^*=\phi
\end{cases}[/math]
This allows us to express the term:
[math]\frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)}=\biggl[\frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p^*\, \theta^*\, \phi^*)}\biggr]^{-1}=\biggl[\frac{\partial (p^*\, \sin{\theta^*}\, \cos{\phi^*}p^*\, \sin{\theta^*}\, \sin{\phi^*}p^*\, \cos{\theta^*})}{\partial p^*\, \partial \theta^*\, \partial \phi^*}\biggr]^{-1}[/math]
[math]\frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)}=\biggl[ \frac{d (p^{*-1})\, d(\cos{\theta^{*}}^{-1})} {d p^*\, d\theta^*}\biggr]=\frac{1}{p^{*2}\sin{\theta^*}}[/math]
Again, similarly
[math]\frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)}=p^2\, \sin{\theta}[/math]
To find the middle component in the chain rule expansion,
[math]\left( \begin{matrix} E^* \\ p^*_x \\ p^*_y \\ p^*_z\end{matrix} \right)=\left(\begin{matrix}\gamma & 0 & 0 & -\beta \gamma\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta\gamma & 0 & 0 & \gamma \end{matrix} \right) . \left( \begin{matrix}E\\ p_x \\ p_y\\ p_z\end{matrix} \right)[/math]
which gives,
[math]\Longrightarrow\begin{cases}
E^*=\gamma E-\beta \gamma^* p_z \\
p^*_z=-\beta \gamma\, E+\gamma\, p_z
\end{cases}[/math]
[math]\frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)}=\frac{\partial p^*_z}{\partial p_z}=\frac{\partial (-\beta \gamma\, E+\gamma\, p_z)}{\partial p_z}=-\beta \gamma \,\frac{\partial E}{\partial p_z}+\gamma[/math]
We can use the relativistic definition of the total Energy,
[math]E=\sqrt{p^2+m^2}=\sqrt{p_x^2+p_y^2+p_z^2+m^2}[/math]
[math]\Rightarrow \frac{\partial p^*_z}{\partial p_z}=\frac{\sqrt {p_x^2+p_y^2+p_z^2+m^2}} {\partial p_z}=\frac{p_z}{\sqrt {p_x^2+p_y^2+p_z^2+m^2}}=\frac{p_z}{E}[/math]
[math]\frac{\partial p^*_z}{\partial p_z}=-\beta \gamma \frac{\partial E}{\partial p_z}+\gamma=-\beta \gamma \frac{p_z}{E}+\gamma[/math]
Then using the fact that
[math]E^*\equiv \gamma E-\beta \gamma\, p_z [/math]
[math]\frac{\partial p^*_z}{\partial p_z}=-\beta \gamma \frac{p_z}{E}+\frac{\gamma\, E}{E}=\frac{E^*}{E}[/math]
Final Expression
Using the values found above, our expression becomes:
[math]\frac{\partial (p^*\, \cos{\theta^*)}}{\partial (p^*\, \theta^*\, \phi^*)} \frac{\partial (p^*\, \theta^*\, \phi^*)}{\partial (p^*_x\, p^*_y\, p^*_z)} \frac{\partial (p^*_x\, p^*_y\, p^*_z)}{\partial (p_x\, p_y\, p_z)} \frac{\partial (p_x\, p_y\, p_z)}{\partial (p\, \theta\, \phi)} \frac{\partial (p\, \theta\, \phi)}{\partial (p\, \cos{\theta})}=\frac{\partial (p^*\, \cos{\theta^*})}{\partial (p\, \cos{\theta})}[/math]
This gives,
[math][/math]
| [math]\Longrightarrow \frac{\partial ^2\sigma(p,\, \theta ,\, \phi)}{\partial p\,\partial \Omega} =\frac{\partial ^2\sigma^*(p^*,\, \theta^* ,\, \phi^*)}{\partial p^*\, \partial \Omega^*} \frac{p^2E^*}{p^{*2}E}[/math]
|
