Scattering Cross Section
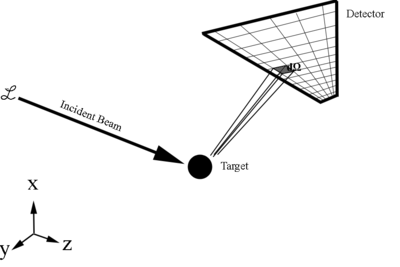
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section[/math]
Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
[math]\sigma=\frac{N}{\mathcal L}=constant\ number[/math]
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations
[math]\therefore\ \sigma_{CM}=\sigma_{Lab}[/math]
[math]d\sigma=I_{lab}(\theta_{lab},\ \phi_{lab})\, d\Omega_{lab}=I_{CM}(\theta_{CM},\ \phi_{CM})\, d\Omega_{CM}[/math]
This is that the number of particles going into the solid-angle element d\Omega and having a moentum between p and p+dp be the same as the number going into the correspoiding solid-angle element d\Omega^* and having a corresponding momentum between p^* and p*+dp*
[math]\left( \begin{matrix} E^* \\ p^*_{x} \\ p^*_{y} \\ p^*_{z}\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E_{1}+E_{2}\\ p_{1(x)}+p_{2(x)} \\ p_{1(y)}+p_{2(y)} \\ p_{1(z)}+p_{2(z)}\end{matrix} \right)[/math]
