|
|
| Line 140: |
Line 140: |
| | | | |
| | | | |
| − | | + | We can use the fact that, |
| − | <center><math>=\frac{\partial p^*_z}{\partial p_z}=\frac{\partial (-\beta^* \gamma^*E+\gamma^* p_z)}{\partial p_z}=-\beta^* \gamma^*\frac{\partial E}{\partial p_z}+\gamma^*</math></center> | + | <center><math>=\frac{\partial E^*}{\partial E}=\frac{\partial (\gamma^* E-\beta^* \gamma^* p_z )}{\partial E}=-\beta^* \gamma^*\frac{\partial p_z}{\partial p_z}+\gamma^*</math></center> |
Revision as of 15:20, 3 February 2016
Scattering Cross Section
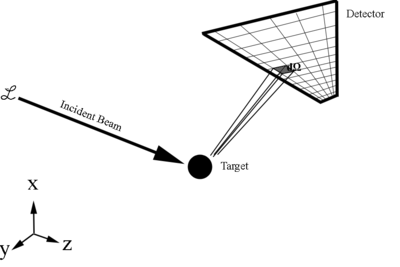
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\Rightarrow \sigma=\int\limits_{\theta=0}^{\pi} \int\limits_{\phi=0}^{2\pi} \left(\frac{d\sigma}{d\Omega}\right)\ \sin{\theta}\,d\theta\,d\phi =\frac{N}{\mathcal L}\equiv total\ scattering\ cross\ section[/math]
Since this is just a ratio of detected particles to total particles, this gives the cross section as a relative probablity of a scattering, or reaction, to occur.
Transforming Cross Section Between Frames
Transforming the cross section between two different frames of reference has the condition that the quantity must be equal in both frames. This is due to the fact that
[math]\sigma=\frac{N}{\mathcal L}=constant\ number[/math]
This makes the total cross section a Lorentz invariant in that it is not effected by any relativistic transformations
[math]\therefore\ \sigma_{CM}=\sigma_{Lab}[/math]
This implies that the number of particles going into the solid-angle element d ΩLab and having a momentum between pLab and pLab+dpLabbe the same as the number going into the corresponding solid-angle element dΩCM and having a corresponding momentum between pCM and pCM+dpCM
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}}dp_{Lab}\,d\Omega_{Lab}=\frac{\partial ^2\sigma_{CM}}{\partial p_{CM}\,\partial \Omega_{CM}}dp_{CM}\, d\Omega_{CM}[/math]
[math]where\ d\Omega=\sin{\theta}\,d\theta\,d\phi[/math]
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}}\partial p_{Lab}\,\sin{\theta_{Lab}}\,d\theta_{Lab}\,d\phi_{Lab}=\frac{d^2\sigma_{CM}}{dp_{CM}\, d\Omega_{CM}}dp_{CM}\, \sin{\theta_{CM}}\,d\theta_{CM}\,d\phi_{CM}[/math]
As shown earlier,
[math]\phi_{Lab}=\phi_{CM}[/math]
[math]\Rightarrow\ d\phi_{Lab}=d\phi_{CM}[/math]
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}} dp_{Lab}\,\sin{\theta_{Lab}}\,d\theta_{Lab}=\frac{\partial ^2\sigma_{CM}}{\partial p_{CM}\, \partial \Omega_{CM}}dp_{CM}\, \sin{\theta_{CM}}\,d\theta_{CM}[/math]
We can use the fact that
[math]\sin{\theta}\ d\theta=d(\cos{\theta})[/math]
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}} dp_{Lab}\,d(\cos{\theta_{Lab}})=\frac{\partial ^2\sigma_{CM}}{\partial p_{CM}\, \partial \Omega_{CM}}dp_{CM}\, d(\cos{\theta_{CM}})[/math]
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}} =\frac{\partial ^2\sigma_{CM}}{\partial p_{CM}\, \partial \Omega_{CM}} \frac{dp_{CM}\,d(\cos{\theta_{CM}})}{dp_{Lab}\,d(\cos{\theta_{Lab}})}[/math]
[math]\frac{\partial ^2\sigma_{Lab}}{\partial p_{Lab}\,\partial \Omega_{Lab}} =\frac{\partial ^2\sigma_{CM}}{\partial p_{CM}\, \partial \Omega_{CM}} \frac{\partial (p_{CM}\,\cos{\theta_{CM})}}{\partial (p_{Lab}\,\cos{\theta_{Lab}})}[/math]
We can use the chain rule to find the transformation term on the right hand side:
[math]\frac{\partial (p^*\,\cos{\theta^*)}}{\partial (p^*\theta^*\phi^*)} \frac{\partial (p^*\theta^*\phi^*)}{\partial (p^*_xp^*_yp^*_z)} \frac{\partial (p^*_xp^*_yp^*_z)}{\partial (p_xp_yp_z)} \frac{\partial (p_xp_yp_z)}{\partial (p\theta\phi)} \frac{\partial (p\theta\phi)}{\partial (p\,\cos{\theta})}=\frac{\partial (p^*\cos{\theta^*})}{\partial (p\cos{\theta})}[/math]
[math]\frac{\partial (p^*\cos{\theta^*})} {\partial (p^*\theta^*\phi^*)}=\frac{\partial p^* \sin{\theta^*} \partial \theta^* \partial \phi^*}{\partial p^*\partial \theta^*\partial \phi^*}=\sin{\theta^*}[/math]
Similarly,
[math]\frac{\partial (p\theta\phi)}{\partial (p\,\cos{\theta})}=\frac{1}{\sin{\theta}}[/math]
Using the conversion of cartesian to spherical coordinates we know:
[math]\begin{cases}
p_x=p\sin{\theta}\cos{\phi} \\
p_y=p\sin{\theta}\sin{\phi} \\
p_z=p\cos{\theta}
\end{cases}[/math]
and the fact that as was shown earlier, that
[math]\begin{cases}
p^*_x=p_x \\
p^*_y=p_y \\
\phi^*=\phi
\end{cases}[/math]
This allows us to express the term:
[math]\frac{\partial (p^*\theta^*\phi^*)}{\partial (p^*_xp^*_yp^*_z)}=\biggl[\frac{\partial (p^*_xp^*_yp^*_z)}{\partial (p^*\theta^*\phi^*)}\biggr]^{-1}=\biggl[\frac{\partial (p^*\sin{\theta^*}\cos{\phi^*}p^*\sin{\theta^*}\sin{\phi^*}p^*\cos{\theta^*})}{\partial p^*\partial \theta^*\partial \phi^*}\biggr]^{-1}[/math]
[math]\frac{\partial (p^*\theta^*\phi^*)}{\partial (p^*_xp^*_yp^*_z)}=\biggl[ \frac{\partial p^{*-1}\cos{\theta^{*}}^{-1}} {\partial p\,d\theta^*}\biggr]=\frac{1}{p^{*2}\sin{\theta^*}}[/math]
Again, similarly
[math]\frac{\partial (p_xp_yp_z)}{\partial (p\theta\phi)}=p^2\sin{\theta}[/math]
To find the middle component in the chain rule expansion,
[math]\left( \begin{matrix} E^* \\ p^*_x \\ p^*_y \\ p^*_z\end{matrix} \right)=\left(\begin{matrix}\gamma^* & 0 & 0 & -\beta^* \gamma^*\\0 & 1 & 0 & 0 \\ 0 & 0 & 1 &0 \\ -\beta^*\gamma^* & 0 & 0 & \gamma^* \end{matrix} \right) . \left( \begin{matrix}E\\ p_x \\ p_y\\ p_z\end{matrix} \right)[/math]
which gives,
[math]\Longrightarrow\begin{cases}
E^*=\gamma^* E-\beta^* \gamma^* p_z \\
p^*_z=-\beta^* \gamma^*E+\gamma^* p_z
\end{cases}[/math]
[math]\frac{\partial (p^*_xp^*_yp^*_z)}{\partial (p_xp_yp_z)}=\frac{\partial p^*_z}{\partial p_z}=\frac{\partial (-\beta^* \gamma^*E+\gamma^* p_z)}{\partial p_z}=-\beta^* \gamma^*\frac{\partial E}{\partial p_z}+\gamma^*[/math]
We can use the fact that,
[math]=\frac{\partial E^*}{\partial E}=\frac{\partial (\gamma^* E-\beta^* \gamma^* p_z )}{\partial E}=-\beta^* \gamma^*\frac{\partial p_z}{\partial p_z}+\gamma^*[/math]
