Difference between revisions of "Sadiq Proposal Defense"
| Line 98: | Line 98: | ||
So, <math>\mathbf{\sigma}</math> matrix can be written as: | So, <math>\mathbf{\sigma}</math> matrix can be written as: | ||
<math> | <math> | ||
| − | \mathbf{ \sigma}_{quad} = | + | \mathbf{\sigma}_{quad} = |
\begin{pmatrix} | \begin{pmatrix} | ||
\sigma_{quad, x} & \sigma_{quad, xx'} \\ | \sigma_{quad, x} & \sigma_{quad, xx'} \\ | ||
Revision as of 00:00, 22 August 2011
Emittance
What is Emittance
In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.
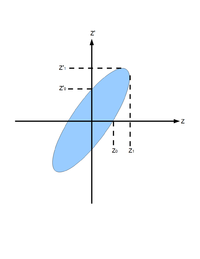
For the convenience of representation, we use to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with . Our transverse beam profile changes along the beam line, it makes is function of , . The angle of a accelerated charge regarding the designed orbit can be defined as:
If we plot vs. , we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.
Measurement of Emittance with Quad Scanning Method
In quadrupole scan method, a quadrupole and a Yttrium Aluminum Garnet (YAG ) screen was used to measure emittance. Magnetic field strength of the quadrupole was changed in the process and corresponding beam shapes were observed on the screen. Transfer matrix of a quadrupole magnet under thin lens approximation:
Here, is quadrupole strength, is quadrupole magnet thickness, and f is quadrupole focal length. for x-plane, and for y-plane. Transfer matrix of a drift space between quadrupole and screen:
Here, () is the distance from the center of the quadrupole to the screen. Transfer matrix of the scanned region is:
is related with the beam matrix as:
Since:
So, matrix can be written as:
Substituting this give:
References
<references/>
Using APA reference style.
Go back: Positrons