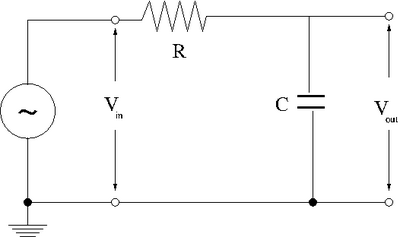
- RC Low-pass filter
1-50 kHz filter (20 pnts)
- Design a low-pass RC filter with a break point between 1-50 kHz. The break point is the frequency at which the filter starts to attenuate the AC signal. For a Low pass filter, AC signals with a frequency above 1-50 kHz will start to be attenuated (not passed).
- Now construct the circuit using a non-polar capacitor.
- use a sinusoidal variable frequency oscillator to provide an input voltage to your filter.
- Measure the input and output voltages for at least 8 different frequencies which span the frequency range from 1 Hz to 1 MHz.
- Graph the [math]\log \left(\frac{V_{out}}{V_{in}} \right)[/math] -vs- [math]\log (\nu)[/math]
phase shift (10 pnts)
- measure the phase shift between [math]V_{in}[/math] and [math]V_{out}[/math]
Questions
- compare the theoretical and experimentally measured break frequencies. (5 pnts)
- Calculate and expression for [math]\frac{V_{out}}{ V_{in}}[/math] as a function of [math]\nu[/math], [math]R[/math], and [math]C[/math]. The Gain is defined as the ratio of [math]V_{out}[/math] to [math]V_{in}[/math].(5 pnts)
- Compare the theoretical and experimental value for the phase shift [math]\theta[/math]. (5 pnts)
- Sketch the phasor diagram for [math]V_{in}[/math],[math] V_{out}[/math], [math]V_{R}[/math], and [math]V_{C}[/math]. Put the current [math]i[/math] along the real voltage axis. (30 pnts)
- what is the phase shift [math]\theta[/math] for a DC input and a very-high frequency input?(5 pnts)
- calculate and expression for the phase shift [math]\theta[/math] as a function of [math]\nu[/math], [math]R[/math], [math]C[/math] and graph [math]\theta[/math] -vs [math]\nu[/math]. (20 pnts)
Forest_Electronic_Instrumentation_and_Measurement
