Difference between revisions of "LB Thesis Thin Window Analysis"
| Line 53: | Line 53: | ||
<math> \sigma_{N} = \sqrt{\sigma_{I}^2 + \sigma_{B}^2} </math> | <math> \sigma_{N} = \sqrt{\sigma_{I}^2 + \sigma_{B}^2} </math> | ||
| + | |||
| + | This is the general method for finding the number of counts for a background subtracted signal within a region of interest. | ||
Revision as of 17:01, 29 November 2017
This will be a detailed explanation of how to trace the isotope of interest's activity back to its original value. The sample of interest here is the oven ash sample with inventory number 170063. The measurement was made on Detector A at the IAC and it was a split run using a Co-60 flag to denote the changing of samples between a pure selenium sample and a mixture of selenium and sage ash. The target information can be found below:
Nickel Foil: 0.2783g
Outer Se Pellets: 0.0971g
Sage Ash: 0.5111g
Inner Se Pellet: 0.0523g
Thin Window Histograms
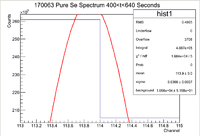
Since the resolution of Detector A at the IAC is about 1 keV, the window in which the signal is viewed should have a width of 2 (whether you plot channel number or energy along the horizontal axis). The signals were fit with a function of the form
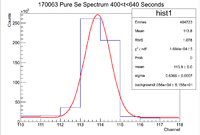
Here, the constant value is to assess the value for the background. The background must be removed from the signal in order to have a more accurate analysis as it is not a part of the signal that we are interested in. Below are sample plots of the original signal and the signal viewed in a thin 2 channel window:
This signal corresponds to the 103 keV line of Se-81. I plotted channel number instead of energy to maintain integer bins and avoid a picket fencing effect in the signal.
In looking at the thin window, the total number of counts within the window is given by the "Integral" value in the statistics box, which I will denote as I.
Since this is a counting experiment, the error in the signal will be given by
Dealing With Background
Now that I have discussed how to get the number of counts along with the uncertainty in the number of counts, I will now discuss how to remove the background from a signal.
In the statistics box, there is a value called "background" which corresponds to the constant value in the fit function. To removed the background from the number of counts in the statistics box, we must integrate the "background" value across the region of interest. In other words
Since the "background" value in the statistics box has an error with it and by integrating we are essentially just multiplying by a constant, so in this case
Now that we have a value for the background along with its uncertainty, we can find the true signal of interest within the window. To find this use the relations
This is the general method for finding the number of counts for a background subtracted signal within a region of interest.