Difference between revisions of "LB Thesis Thin Window Analysis"
| (49 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
Inner Se Pellet: 0.0523g | Inner Se Pellet: 0.0523g | ||
| + | Half Life of Se-81: 57.28 +/- 0.02 Minutes | ||
| + | |||
| + | Decay Constant: <math> 2.016838863 \times 10^{-4} \pm 1.173672523 \times 10^{-9} \frac{1}{seconds} </math> | ||
| + | |||
==Thin Window Histograms== | ==Thin Window Histograms== | ||
| + | Each histogram has its number of counts weighted by the mass of the sample. | ||
| + | |||
Since the resolution of Detector A at the IAC is about 1 keV, the window in which the signal is viewed should have a width of 2 (whether you plot channel number or energy along the horizontal axis). The signals were fit with a function of the form | Since the resolution of Detector A at the IAC is about 1 keV, the window in which the signal is viewed should have a width of 2 (whether you plot channel number or energy along the horizontal axis). The signals were fit with a function of the form | ||
| Line 30: | Line 36: | ||
<math> Stats Box Integral = I </math> | <math> Stats Box Integral = I </math> | ||
| − | + | To find the error in the signal, expand the window by 1 channel on each side and subtract the stats box integrals from these 2 different windows. In other words the intrinsic error will be | |
| − | <math> \sigma_{I} = \ | + | <math> \sigma_{I} = \frac{I_{Expanded}-I}{I} </math> |
==Dealing With Background== | ==Dealing With Background== | ||
| Line 38: | Line 44: | ||
Now that I have discussed how to get the number of counts along with the uncertainty in the number of counts, I will now discuss how to remove the background from a signal. | Now that I have discussed how to get the number of counts along with the uncertainty in the number of counts, I will now discuss how to remove the background from a signal. | ||
| − | In the statistics box, there is a value called "background" which corresponds to the constant value in the fit function. To removed the background from the number of counts, we must integrate the "background" value across the region of interest. In other words | + | In the statistics box, there is a value called "background" which corresponds to the constant value in the fit function. To removed the background from the number of counts in the statistics box, we must integrate the "background" value across the region of interest. In other words |
| + | |||
| + | <math> Background = B = \int_{113}^{115} C d(Channel) = C(115-113) </math> | ||
| + | |||
| + | |||
| + | Since the "background" value in the statistics box has an error with it and by integrating we are essentially just multiplying by a constant, so in this case | ||
| + | |||
| + | <math> \sigma_{B} = \int_{113}^{115}\sigma_{C} d(Channel) = \sigma_{C}(115-113) </math> | ||
| + | |||
| + | |||
| + | Now that we have a value for the background along with its uncertainty, we can find the true signal of interest within the window. To find this use the relations | ||
| + | |||
| + | <math> True Signal = N = I - B </math> | ||
| + | |||
| + | <math> \sigma_{N} = \sqrt{\sigma_{I}^2 + \sigma_{B}^2} </math> | ||
| + | |||
| + | Now we have values for the number of counts without background along with the uncertainty in that value. | ||
| + | |||
| + | |||
| + | ==Decay During the Measurement== | ||
| + | |||
| + | It is worth noting that since the half life of the sample is rather short that by measuring for roughly 5 minutes for each sample, the activity at the beginning of the measurement and the activity at the end are not the same. For example, if we assume some initial activity, then look at the activity after five minutes it will be slightly lower. In other words, assuming a run time of 300 seconds | ||
| + | |||
| + | <math> A = A_0 \times e^{-\lambda t} = A_0 \times e^{-\lambda \times 300} = 0.94 \times A_0</math> | ||
| + | |||
| + | This shows that the activity drops by about 6 percent during a measurement of 5 minutes. To remedy this, one can use the fact that the measurement being made is actually integrating the true value of the activity over the time of the measurement. Or | ||
| + | |||
| + | <math> A_{Measure} = \frac{\int_{0}^{t}A_{True}\times e^{-\lambda t}dt}{t} </math> | ||
| + | |||
| + | By integrating and solving for the true activity, we find that | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda t}\times A_{Measure}\times t \times \lambda}{e^{\lambda t} -1} </math> | ||
| + | |||
| + | The error in this value is dominated by the error in the measured value, so the error in the true activity can be found by | ||
| + | |||
| + | <math> \sigma_{A_{True}} = \sqrt{(\frac{t\times e^{\lambda t} \times \lambda \times \sigma_{A_{Measure}}}{e^{\lambda t}-1})^2 + \frac{e^{\lambda t}(A t e^{\lambda t} - \lambda^2 - A t + A t \lambda)}{(e^{\lambda t}-1)^2} \times \sigma_{\lambda}^2} </math> | ||
| + | |||
| + | ==Dead Time== | ||
| + | Dead time helps account for the number of counts that may have been lost because the data acquisition system was too busy recording. A count rate vs. % Dead time plot was made that is shown below: | ||
| + | |||
| + | {| border="3" cellpadding="5" cellspacing="0" | ||
| + | ||Count Rate (Hz) || % Dead | ||
| + | |- | ||
| + | ||129.47 +/- 7.84 || 0.24 +/- 0.10 | ||
| + | |- | ||
| + | ||154.33 +/- 10.36 || 0.29 +/- 0.11 | ||
| + | |- | ||
| + | ||194.83 +/- 8.36 || 0.41 +/- 0.11 | ||
| + | |- | ||
| + | ||253.69 +/- 14.05 || 0.51 +/- 0.18 | ||
| + | |- | ||
| + | ||257.11 +/- 11.24 || 0.53 +/- 0.14 | ||
| + | |- | ||
| + | ||338.8 +/- 11.68 || 0.65 +/- 0.15 | ||
| + | |- | ||
| + | ||477.61 +/- 15.06 || 0.84 +/- 0.16 | ||
| + | |- | ||
| + | ||619.3 +/- 10.56 || 1.34 +/- 0.18 | ||
| + | |- | ||
| + | ||680.83 +/- 17.5 || 1.33 +/- 0.23 | ||
| + | |- | ||
| + | ||807.37 +/- 15.85 || 1.55 +/- 0.18 | ||
| + | |- | ||
| + | ||889.6 +/- 16.22 || 1.65 +/- 0.34 | ||
| + | |- | ||
| + | ||1051.33 +/- 26.74 || 1.92 +/- 0.26 | ||
| + | |- | ||
| + | ||1213.93 +/- 23.62 || 2.26 +/- 0.33 | ||
| + | |- | ||
| + | || 1389.45 +/- 24.75 || 2.53 +/- 0.31 | ||
| + | |- | ||
| + | ||1628.47 +/- 17.17 || 3.06 +/- 0.30 | ||
| + | |- | ||
| + | ||2084.6 +/- 33.77 || 3.95 +/- 0.42 | ||
| + | |- | ||
| + | ||2576.5 +/- 31.53 || 5.06 +/- 0.39 | ||
| + | |- | ||
| + | ||3058.20 +/- 35.62 || 5.87 +/- 0.54 | ||
| + | |- | ||
| + | ||3362.13 +/- 23.12 || 6.59 +/- 0.43 | ||
| + | |- | ||
| + | ||4067.2 +/- 45.37 || 8.18 +/- 0.66 | ||
| + | |- | ||
| + | ||4564.37 +/- 61.94 || 9.09 +/- 0.60 | ||
| + | |- | ||
| + | ||5511.6 +/- 64.60 || 10.86 +/- 0.85 | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | |||
| + | Below is a plot of the data | ||
| + | |||
| + | [[File:LB DeadTimevsCountRate DetA.png|200px]] | ||
| + | |||
| + | To account for the dead time, look at the total number of entries in the histogram and divide by the run time to get an average count rate. Then use the table to estimate the dead time. Once the dead time has been estimated, the correction factor is given by | ||
| + | |||
| + | <math> Dead Time Correction = \frac{1}{1-Dead Time} </math> | ||
| + | |||
| + | ==Thin Method Applied== | ||
| + | Now I will apply this method to try to trace an activity back to a previously measured activity. In this example I will be using two measurements. There was a measurement taken at some time and 700 seconds later another measurement of the same sample was measured. I want to know if using this method I can trace back the activity measured 700 seconds later to the activity measured initially. First begin by finding the initial activity of the sample. | ||
| + | |||
| + | For a reference to the tables of histograms and statistical information, visit | ||
| + | |||
| + | [[Se170063 Thin Window Analysis]] | ||
| + | |||
| + | Below is a plot of the signal of interest initially. | ||
| + | |||
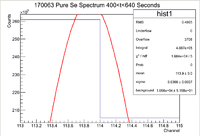
| + | [[File:170063 PureSe ThinWindow 400 640Sec.png|200px]] | ||
| + | |||
| + | From here we can see that the integral in the statistics box gives | ||
| + | |||
| + | <math> I = 466700 Counts </math> | ||
| + | |||
| + | This would mean that the error in the integral is | ||
| + | |||
| + | <math> \sigma_{I} = \sqrt{I} = 683 Counts </math> | ||
| + | |||
| + | Now we must account for the background in the region. The value of the constant is given by | ||
| + | |||
| + | <math> C \pm \sigma_{C} = 10560 \pm 51.58 Counts </math> | ||
| + | |||
| + | By integrating these over the region of interest (which is essentially just multiplying the constant by 2) gives | ||
| + | |||
| + | <math> B \pm \sigma_{B} = 21120 \pm 103.16 Counts </math> | ||
| + | |||
| + | Now we can find the true number of counts for the signal of interest | ||
| + | |||
| + | <math> N = I - B = 445580 Counts </math> | ||
| + | |||
| + | while the error is | ||
| + | |||
| + | <math> \sigma_N = \sqrt{\sigma_I^2 + \sigma_B^2} = \sqrt{683^2 + 103.16^2} = 690.75 Counts </math> | ||
| + | |||
| + | Now dividing by the total time to give the activity of the sample we get | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{445580}{240} \pm \frac{690.75}{240} = 1856.58 \pm 2.88 Hz </math> | ||
| + | |||
| + | Now we have the measured value for the activity. Finding the true value, we get | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 240} \times 1856.58 \times 240 \times \lambda}{e^{\lambda \times 240}-1} = 1901.88 Hz</math> | ||
| + | |||
| + | Now find the error in the true value of the activity | ||
| + | |||
| + | <math> \sigma_{A_{True}} = \frac{240 \times \lambda \times \sigma_{A_{Measure}} \times e^{\lambda \times 240}}{e^{\lambda \times 240}-1} = 2.85 Hz</math> | ||
| + | |||
| + | Now we have the true value for the activity along with its associated error. Finally, we must deal with the dead time. Below is a plot that shows the total number of entries in the histogram. | ||
| + | |||
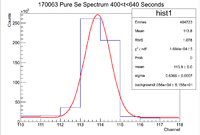
| + | [[File:170063 PureSe 400 640Sec OGWindow.png|200px]] | ||
| + | |||
| + | From here we can see that the total number of counts in the entire histogram is 404723 Counts. Now divide by time to find the average count rate over the 240 second measurement time | ||
| + | |||
| + | <math> Average Count Rate = 404723/240 = 1686.35 Hz </math> | ||
| + | |||
| + | The closest activity with a corresponding dead time above is 3.06 +/- 0.30 Now using this we must correct for the dead time. | ||
| + | |||
| + | Computing the correction factor, we get | ||
| + | |||
| + | <math> \frac{1}{1-0.0306} = 1.03 </math> | ||
| + | |||
| + | So the true activity of the sample is | ||
| + | |||
| + | <math> A_{True} = 1.03 \times 1901.88 = 1958.94 Hz </math> | ||
| + | |||
| + | Now we can find the error in the dead time correction by using the standard error propagation method | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{(1-DT)^2} = \frac{0.003}{(1-0.0306)^2} = 0.003 </math> | ||
| + | |||
| + | Now we can find the error in the true number activity with the dead time accounted for (here DTC stands for dead time correction) | ||
| + | |||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the true signal accounting for dead time is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A{True}} = 1958.94 \pm 6.42 Hz </math> | ||
| + | |||
| + | Next we move on to the measurement that was made 700 seconds later. The first step here is to repeat the analysis as about, but we must correct the activity back to the same time as the first measurement to compare the activities. Below is are histograms of the measurement made 700 seconds later | ||
| + | |||
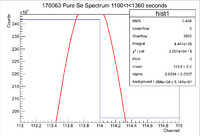
| + | [[File:170063 PureSe 1100 1360Sec ThinWindow.png|200px]] | ||
| + | [[File:170063 PureSe 1100 1360 Seconds OGWindow.png|200px]] | ||
| + | |||
| + | From here we can see that the statistics box gives an integral of | ||
| + | |||
| + | |||
| + | <math> I = 444100 Counts </math> | ||
| + | |||
| + | This would mean that the error in the integral is | ||
| + | |||
| + | <math> \sigma_{I} = \sqrt{I} = 666 Counts </math> | ||
| + | |||
| + | Now we must account for the background in the region. The value of the constant is given by | ||
| + | |||
| + | <math> C \pm \sigma_{C} = 10560 \pm 51.41 Counts </math> | ||
| + | |||
| + | By integrating these over the region of interest (which is essentially just multiplying the constant by 2) gives | ||
| + | |||
| + | <math> B \pm \sigma_{B} = 21120 \pm 102.82 Counts </math> | ||
| + | |||
| + | Now we can find the true number of counts for the signal of interest | ||
| + | |||
| + | <math> N = I - B = 422980 Counts </math> | ||
| + | |||
| + | while the error is | ||
| + | |||
| + | <math> \sigma_N = \sqrt{\sigma_I^2 + \sigma_B^2} = \sqrt{666^2 + 102.82^2} = 673.89 Counts </math> | ||
| + | |||
| + | Now dividing by the total time to give the activity of the sample we get | ||
| + | |||
| + | <math> A_{Measure} \pm \sigma_{A_{Measure}} = \frac{422980}{260} \pm \frac{673.89}{260} = 1626.85 \pm 2.59 Hz </math> | ||
| + | |||
| + | Now we have the measured value for the activity. Finding the true value, we get | ||
| + | |||
| + | <math> A_{True} = \frac{e^{\lambda \times 260} \times 1626.85 \times 260 \times \lambda}{e^{\lambda \times 260}-1} = 1669.88 Hz</math> | ||
| + | |||
| + | Now find the error in the true value of the activity | ||
| + | |||
| + | <math> \sigma_{A_{True}} = \frac{260 \times \lambda \times \sigma_{A_{Measure}} \times e^{\lambda \times 260}}{e^{\lambda \times 260}-1} = 2.66 Hz</math> | ||
| + | |||
| + | Now we have the true value for the activity along with its associated error. Finally, we must deal with the dead time. Below is a plot that shows the total number of entries in the histogram. | ||
| + | |||
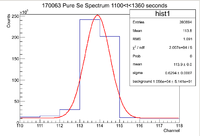
| + | [[File:170063 PureSe 1100 1360 Seconds OGWindow.png|200px]] | ||
| + | |||
| + | From here we can see that the total number of counts in the entire histogram is 393894 Counts. Now divide by time to find the average count rate over the 260 second measurement time | ||
| + | |||
| + | <math> Average Count Rate = 393894/260 = 1514.98 Hz </math> | ||
| + | |||
| + | The closest activity with a corresponding dead time above is 2.53 +/- 0.31 Now using this we must correct for the dead time. | ||
| + | |||
| + | Computing the correction factor, we get | ||
| + | |||
| + | <math> \frac{1}{1-0.0253} = 1.03 </math> | ||
| + | |||
| + | So the true activity of the sample is | ||
| + | |||
| + | <math> A_{True} = 1.03 \times 1669.88 = 1719.98 Hz </math> | ||
| + | |||
| + | Now we can find the error in the dead time correction by using the standard error propagation method | ||
| + | |||
| + | <math> \sigma_{DTC} = \frac{\sigma_{DT}}{(1-DT)^2} = \frac{0.0031}{(1-0.0253)^2} = 0.003 </math> | ||
| + | |||
| + | Now we can find the error in the true number activity with the dead time accounted for (here DTC stands for dead time correction) | ||
| + | <math> \sigma_{A_{True}^{DT}} = \sqrt{\frac{\sigma_{A_{True}^{DT}}^2}{(1-DT)^2} + \frac{A_{True}^2 \sigma_{DT}^2}{(1-DT)^4}} </math> | ||
| + | |||
| + | So the true signal accounting for dead time is | ||
| + | |||
| + | <math> A_{True} \pm \sigma_{A{True}} = 1719.98 \pm 5.71 Hz </math> | ||
| + | |||
| + | Now that we have the signal of interest we must trace back by 700 seconds by using the standard radioactive decay equation | ||
| + | |||
| + | <math>A_{t=400} = 1719.98 e^{\lambda \times 700} = 1980.78 Hz</math> | ||
| + | |||
| + | <math> \sigma_{A_{t=400}} = \sigma_{A_{True}} \times e^{\lambda \times 700} = 6.58 Hz </math> | ||
| + | |||
| + | So now we have a time corrected, dead time corrected value of | ||
| + | |||
| + | <math> 1980.78 \pm 6.58 Hz </math> | ||
| − | + | Notice that this value and the original activity are within two standard deviations of each other, meaning they are statistically the same. | |
Latest revision as of 19:25, 10 January 2018
This will be a detailed explanation of how to trace the isotope of interest's activity back to its original value. The sample of interest here is the oven ash sample with inventory number 170063. The measurement was made on Detector A at the IAC and it was a split run using a Co-60 flag to denote the changing of samples between a pure selenium sample and a mixture of selenium and sage ash. The target information can be found below:
Nickel Foil: 0.2783g
Outer Se Pellets: 0.0971g
Sage Ash: 0.5111g
Inner Se Pellet: 0.0523g
Half Life of Se-81: 57.28 +/- 0.02 Minutes
Decay Constant:
Thin Window Histograms
Each histogram has its number of counts weighted by the mass of the sample.
Since the resolution of Detector A at the IAC is about 1 keV, the window in which the signal is viewed should have a width of 2 (whether you plot channel number or energy along the horizontal axis). The signals were fit with a function of the form
Here, the constant value is to assess the value for the background. The background must be removed from the signal in order to have a more accurate analysis as it is not a part of the signal that we are interested in. Below are sample plots of the original signal and the signal viewed in a thin 2 channel window:
This signal corresponds to the 103 keV line of Se-81. I plotted channel number instead of energy to maintain integer bins and avoid a picket fencing effect in the signal.
In looking at the thin window, the total number of counts within the window is given by the "Integral" value in the statistics box, which I will denote as I.
To find the error in the signal, expand the window by 1 channel on each side and subtract the stats box integrals from these 2 different windows. In other words the intrinsic error will be
Dealing With Background
Now that I have discussed how to get the number of counts along with the uncertainty in the number of counts, I will now discuss how to remove the background from a signal.
In the statistics box, there is a value called "background" which corresponds to the constant value in the fit function. To removed the background from the number of counts in the statistics box, we must integrate the "background" value across the region of interest. In other words
Since the "background" value in the statistics box has an error with it and by integrating we are essentially just multiplying by a constant, so in this case
Now that we have a value for the background along with its uncertainty, we can find the true signal of interest within the window. To find this use the relations
Now we have values for the number of counts without background along with the uncertainty in that value.
Decay During the Measurement
It is worth noting that since the half life of the sample is rather short that by measuring for roughly 5 minutes for each sample, the activity at the beginning of the measurement and the activity at the end are not the same. For example, if we assume some initial activity, then look at the activity after five minutes it will be slightly lower. In other words, assuming a run time of 300 seconds
This shows that the activity drops by about 6 percent during a measurement of 5 minutes. To remedy this, one can use the fact that the measurement being made is actually integrating the true value of the activity over the time of the measurement. Or
By integrating and solving for the true activity, we find that
The error in this value is dominated by the error in the measured value, so the error in the true activity can be found by
Dead Time
Dead time helps account for the number of counts that may have been lost because the data acquisition system was too busy recording. A count rate vs. % Dead time plot was made that is shown below:
| Count Rate (Hz) | % Dead |
| 129.47 +/- 7.84 | 0.24 +/- 0.10 |
| 154.33 +/- 10.36 | 0.29 +/- 0.11 |
| 194.83 +/- 8.36 | 0.41 +/- 0.11 |
| 253.69 +/- 14.05 | 0.51 +/- 0.18 |
| 257.11 +/- 11.24 | 0.53 +/- 0.14 |
| 338.8 +/- 11.68 | 0.65 +/- 0.15 |
| 477.61 +/- 15.06 | 0.84 +/- 0.16 |
| 619.3 +/- 10.56 | 1.34 +/- 0.18 |
| 680.83 +/- 17.5 | 1.33 +/- 0.23 |
| 807.37 +/- 15.85 | 1.55 +/- 0.18 |
| 889.6 +/- 16.22 | 1.65 +/- 0.34 |
| 1051.33 +/- 26.74 | 1.92 +/- 0.26 |
| 1213.93 +/- 23.62 | 2.26 +/- 0.33 |
| 1389.45 +/- 24.75 | 2.53 +/- 0.31 |
| 1628.47 +/- 17.17 | 3.06 +/- 0.30 |
| 2084.6 +/- 33.77 | 3.95 +/- 0.42 |
| 2576.5 +/- 31.53 | 5.06 +/- 0.39 |
| 3058.20 +/- 35.62 | 5.87 +/- 0.54 |
| 3362.13 +/- 23.12 | 6.59 +/- 0.43 |
| 4067.2 +/- 45.37 | 8.18 +/- 0.66 |
| 4564.37 +/- 61.94 | 9.09 +/- 0.60 |
| 5511.6 +/- 64.60 | 10.86 +/- 0.85 |
Below is a plot of the data
To account for the dead time, look at the total number of entries in the histogram and divide by the run time to get an average count rate. Then use the table to estimate the dead time. Once the dead time has been estimated, the correction factor is given by
Thin Method Applied
Now I will apply this method to try to trace an activity back to a previously measured activity. In this example I will be using two measurements. There was a measurement taken at some time and 700 seconds later another measurement of the same sample was measured. I want to know if using this method I can trace back the activity measured 700 seconds later to the activity measured initially. First begin by finding the initial activity of the sample.
For a reference to the tables of histograms and statistical information, visit
Below is a plot of the signal of interest initially.
From here we can see that the integral in the statistics box gives
This would mean that the error in the integral is
Now we must account for the background in the region. The value of the constant is given by
By integrating these over the region of interest (which is essentially just multiplying the constant by 2) gives
Now we can find the true number of counts for the signal of interest
while the error is
Now dividing by the total time to give the activity of the sample we get
Now we have the measured value for the activity. Finding the true value, we get
Now find the error in the true value of the activity
Now we have the true value for the activity along with its associated error. Finally, we must deal with the dead time. Below is a plot that shows the total number of entries in the histogram.
From here we can see that the total number of counts in the entire histogram is 404723 Counts. Now divide by time to find the average count rate over the 240 second measurement time
The closest activity with a corresponding dead time above is 3.06 +/- 0.30 Now using this we must correct for the dead time.
Computing the correction factor, we get
So the true activity of the sample is
Now we can find the error in the dead time correction by using the standard error propagation method
Now we can find the error in the true number activity with the dead time accounted for (here DTC stands for dead time correction)
So the true signal accounting for dead time is
Next we move on to the measurement that was made 700 seconds later. The first step here is to repeat the analysis as about, but we must correct the activity back to the same time as the first measurement to compare the activities. Below is are histograms of the measurement made 700 seconds later
From here we can see that the statistics box gives an integral of
This would mean that the error in the integral is
Now we must account for the background in the region. The value of the constant is given by
By integrating these over the region of interest (which is essentially just multiplying the constant by 2) gives
Now we can find the true number of counts for the signal of interest
while the error is
Now dividing by the total time to give the activity of the sample we get
Now we have the measured value for the activity. Finding the true value, we get
Now find the error in the true value of the activity
Now we have the true value for the activity along with its associated error. Finally, we must deal with the dead time. Below is a plot that shows the total number of entries in the histogram.
From here we can see that the total number of counts in the entire histogram is 393894 Counts. Now divide by time to find the average count rate over the 260 second measurement time
The closest activity with a corresponding dead time above is 2.53 +/- 0.31 Now using this we must correct for the dead time.
Computing the correction factor, we get
So the true activity of the sample is
Now we can find the error in the dead time correction by using the standard error propagation method
Now we can find the error in the true number activity with the dead time accounted for (here DTC stands for dead time correction)
So the true signal accounting for dead time is
Now that we have the signal of interest we must trace back by 700 seconds by using the standard radioactive decay equation
So now we have a time corrected, dead time corrected value of
Notice that this value and the original activity are within two standard deviations of each other, meaning they are statistically the same.