Difference between revisions of "Induced Neutron Fission Fragment"
| Line 64: | Line 64: | ||
d (<math> B^9 , B^10</math>)n + 4.36 MeV | d (<math> B^9 , B^10</math>)n + 4.36 MeV | ||
| − | d (<math> Li^7 , Be^7</math>)n - 1.65 MeV | + | d (<math> Li^7 , Be^7</math>)n - 1.65 MeV <ref > Reuss </ref> |
=Neutron energy: types and spectra= | =Neutron energy: types and spectra= | ||
Revision as of 19:23, 18 May 2013
Neutron Emission
They are two typs of neutron sources: Natural neutron sources, and laboratory neutron sources.
- A-Natural Neutron Sources (Intrinsic Sources)
These type of sources are naturally exits, they mainly emit neutrons by spontaneous fission. An examples of they sources are listed in table below.
Some of these sources are created by nuclear reaction in a reactor as it will be discussed below.
| Nuclide | Fission | -decay | Neutron/sec.gram |
| years | years | ||
| years | years | ||
| years | years | ||
| years | years | ||
| years | years | ||
| 66 years | 2.65 years |
- Cf-252
Cl-252 is one of the most commonly used natural source in industry and laboratories. Cf-252 has a continuous neutron spectrum up to 10 MeV that has a Maxwellian distribution, so it can be precisely described by:
T= 1.3 MeV. <ref > Leo</ref>
It is important to notice that 96.9% of all of Cf-252 decays are \alpha decays, and only 3.1 % occur through spontaneous fission. (considering the half life is 85.5 yeas for SF and 2.73 years for alpha decay).<ref > Reuss </ref>
- B- Industrial sources (installed or Laboratory sources)
The production the industrial neutron sources is by particle accelerator, Van de Graaff electrostatic accelerator, or by nuclear reactor. In case of using a particle accelerator, photon activation is one of the methods to produce this type of sources by carefully choosing an appropriate target.
when using Van de Graaff accelerator, it project a deuteron or a proton toward the target to produce neutrons, for example:
d ()n + 1.27 MeV
d ()n + 17.6 MeV
d ()n + 4.36 MeV
d ()n - 1.65 MeV <ref > Reuss </ref>
Neutron energy: types and spectra
Neutron are classified into four types depending on their energy, each type has energy range which may change from one reference to another. The following table shows the types of neutrons, their energy range, and common detective materials.
| Neutron Type | Energy Range | Common detective material(s) |
| Ultracold Neutrons | less than 2*10^-7 | |
| Very Cold Neutrons | 2*10^-7eV =< K.E <= 5*10^-5 eV | |
| Cold Neutrons | 5*10^-5 eV =< K.E. =< 0.025 eV | He-3 |
| Thermal Neutrons | K.E ~_ 0.025 eV | Be-4, Li-6 |
| Epithermal Neutrons | 1 eV =< K.E =< 0.1 keV | |
| Intermediate Neutrons | 1 keV =< K.E =< 0.1 MeV | |
| Fast Neutrons | K.E > 0.1 MeV | U-238, Th-232 |
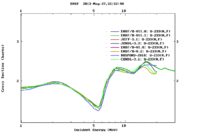
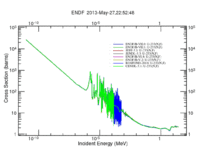
Neutron Induced Fission of U233 Cross Sections
The definition of neutron induced fission cross section is the probability of occurrence of a fission interaction by an incident neutron that has a defined energy. Actinides and lanthanides generally have high fission cross sections compared to those of the rest of periodic table elements; but the cross section values changes with the incident neutron energy. For instance, U-235 has a high fission cross section for thermal neutrons compared to U-238 whose fission cross section is high for fast neutrons. U-233 has relatively high fission cross section values for almost all neutron energy range that starts with thermal neutron and ends with fast neutrons up to more than 30 MeV as shown in the following figure.
The interaction rate of the neutron with the fissionable material depends on the fission cross sections, microscopic and macroscopic fission cross sections, the microscopic cross section defined the effective area for a single nucleus for an interaction, but the macroscopic cross section determines the probability of a neutron to interact when it travels a unit distance in a macroscopic material. The macroscopic and the microscopic cross sections mathematically are related by the following: <ref name="Knief"> Knief R.A., (1992). Nuclear Engineering: Theory and Technology of Commercial Nuclear Power. 2nd ed. e.g. England: Hemisphere Publishing Corporation. </ref>:
Where is the macroscopic cross section and is the microscopic cross section , n is the material (target) atomic density . The macroscopic cross section has the unit of (which is the reciprocal of mean free path).
If a neutron flux () interacts with a material of thickness x, the flux will attenuate inside the material, the process mathematically is represented by the following equation:
So
and the microscopic cross section of the material equals:
The cross section is defined by the following equation :<ref name="Ahmed"/>
where
Where is the number incident particle per uni area per unit time, dN is the average number of particles per unit time that interacted per unit solid angle, and is the solid angle. Since the cross section has an area unit (barn), some authors define this quantity as the area to which the particle is exposed to make an interaction. <ref name="Ahmed">Syed Ahmed, Physics and Engineering of Radiation Detection (Academic Press 2007) </ref> The cross section values are represented as a function of energy that gives the value of the cross section for each energy value and shows the resonance peaks. A theoretical description of the neutron fission cross section curve is not available, but statistically it is possible to evaluate the parameters for an assumption that describes part of the cross section curve within a certain error.<ref name="Hyde"/>
Neutron fission is one of the interactions that commonly takes place spontaneously or under certain experimental conditions. An incident neutron depositing sufficient energy in a nucleus to enable the nucleus to overcome the Coulomb barrier will cause the nucleus to split into fragment ligher nuclei (fragments) and particles. The new products interact with the surrounding medium depending on their energy and the type of the medium that contains them.
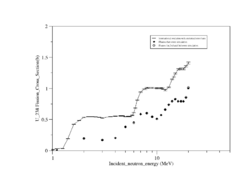
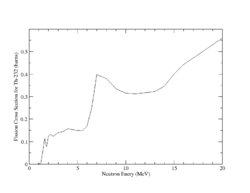
Both U-238 and Th-232 are members of the actinides group. They are characterized by relatively high neutron fission cross sections for fast neutrons with fission thresholds above the thermal neutron energy. The fission reaction in both elements is expected to eject 1-2 neutrons when the incident neutron energy is between 5-10 MeV as shown in Fig.9 and Fig.10.
 |
|
| Fig.9 U 238 fission cross section | Fig.10 Th 232 fission cross section <ref name="endf_Th_232_JEFF1.3">http://www.nndc.bnl.gov/exfor/servlet/E4sMakeE4 </ref> |
<references/>
Read more: http://www.americanessays.com/tool-box/apa-format-citation-generator/#ixzz2P8Ae4GVv