Difference between revisions of "HRRL radiation footprint simulations"
| Line 32: | Line 32: | ||
=== Gulio's measurements=== | === Gulio's measurements=== | ||
| − | 5 detectors at location 13 and 11 saw a dose of 5828 mrad/hr and 164 mrad/hr when accelerator was running with 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width. | + | 5 detectors at location 13 and 11 saw a dose of 5828 mrad/hr and 164 mrad/hr, when accelerator was running with 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width. |
Revision as of 21:37, 24 August 2010
Simulation report
The development of a positron source for JLab using the HRRL requires moving the HRRL to a new location in order to have sufficient room to construct an achomat beam line. The simulation package Geant4 was used to estimate the changes to the radiation footprint that will result from moving the HRRL accelerator cavity near the entrance to the accelerator room. The simulation indicates that moving HRRL to the proposed position will increase the radiation at the doorway to the accelerator room 8.6 times. The simulation also estimates that a 1.2 cm thick lead shielding around the accelerator will reduce the radiation at the door way to its original levels.
Proposed change to Accelerator
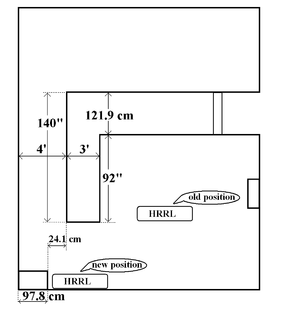
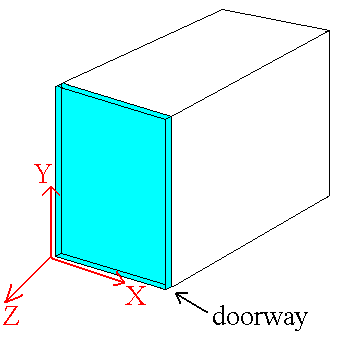
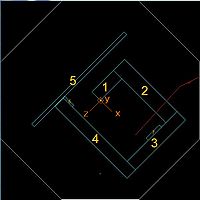
We propose moving the HRRL accelerator cavity from its current location in the center of the room to a corner wall in order to construct a chromatic beam line which will be used in the develop of a positron source for JLab. Below is a picture illustrating the current location of the HRRL cavity and the proposed new location.
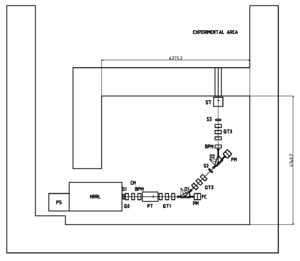
This new position will allow us to install enough quads and dipoles to create an achromatic beam of electrons or positrons. A Tungsten converter will be place close to the HRRL cavity and be used to generate positrons. A setup of two quads will be used before the Tungsten converter in order to focus the incident electron beam on the target. A Faraday Cup is place on the zero port line to measure the beam current and optimize beam transmission prior to inserting a Tungsten converter. A system of 3 quads will be used to collect positrons escaping from the downstream side of the Tungsten converter. The first dipole will separate positrons from the primary electron beam. The remaining beam optics are shown in the beam line drawing below.
Radiation Measurements
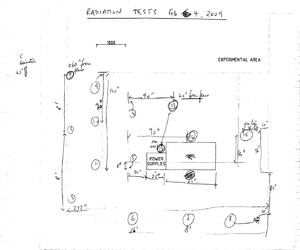
Several measurements of the HRRL's radiation foot print have been done. The first measurements were performed by M. Balzer and G. Stancari on Feb. 4, 2009 using OSL dosimeters at 15 locations within the accelerator room. Two additional measurements were done on May 17, 2010 and July 28, 2010 which measured the dose using Ludlum's ion chamber radiation monitors Model 375/9. The first measurements using OSL dosimeters was done to get a general map of the radiation surrounding the HRRL accelerator. The second set of measurements focused on two locations and looked at how well the radiation scales with the accelerator beam properties in order to establish a guide for extrapolating the dose after moving the cavity to new location. The largest dose rate was observed on a wall at a spot which was at 90 degrees from the center of the accelerator (location 7 shown below). The dose dropped as you moved away from the central region of the accelerator. The OSL measurement at a spot symmetric to that location (location 13) reported a dose that was about an order of magnitude smaller. The second set of measurements focused on location 13 as it will be located in the doorway of the accelerator room after the HRRL is repositioned.
Gulio's measurements
5 detectors at location 13 and 11 saw a dose of 5828 mrad/hr and 164 mrad/hr, when accelerator was running with 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width.
|
Sadiq's measurements
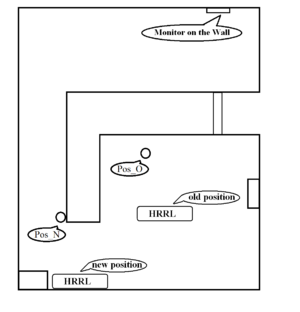
Our measurements are aimed to extrapolate dose rate on monitor on the wall of experimental cell side after shifting the cavity to new location. The idea is the position Pos_O will be shifted to Pos_N after shifting the cavity to new location. The dose rate at Pos_O before shifting should indicate expected dose at Pos_N after shifting the cavity. Assuming relative ratio of dose at Pos_N and on monitor shouldn't change before and after shifting the cavity, we can calculate expected dose rate on monitor after shifting the cavity to new location.
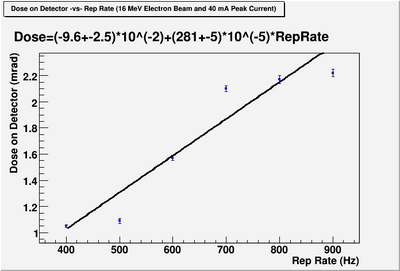
We did radiation measurement to estimate the dose rate on the monitor on the experimental cell side after shifting the cavity to new location. For a beam with electron beam energy of 16 MeV, beam peak current of 40 mA, pulse width full width half max of 150 ns, at the monitor at experimental cell side we would expect dose rate and rap rate relation of:
compare Guilios measurement at spot 11 and 15 mev to your measurement at 16 MeV
ratios of detectors => to get 2 mrad/h at ch. 17 you need ? at ch. 16.
This means we will trip the monitor if our dose at the location in the doorway exceed ? mrad/hr.
Summary of Measurements
1) M. Balzer and Gulio Stancari's measurements: 5 detectors at location 13 and 11 saw a dose of 5828 mrad/hr and 164 mrad/hr when accelerator was running with 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width; 2) A radiation monitor were placed at corner of the door way (Channel 16). Another monotor as trig were at the wall of the experimental cell side (Channel 17). Measurement at July shows: The ratio (Chan16/Chan17) of dose rate at two ranges 200-300. Measurement at May shows: The ratio of dose rate at two ranges 8-27. This is due to at May we had a dipole to divert electron beam and a aluminum, thus we were sending photons to the experimental cell side. At July run, we removed the dipole and had a Faraday Cup at the end of the beam line. Faraday Cup was well shielded.
Simulation results
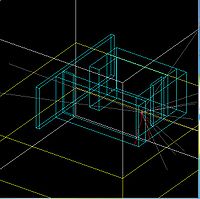
Geometry definitions
Volumes in simulation are show in following figures:
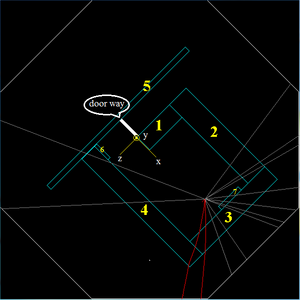
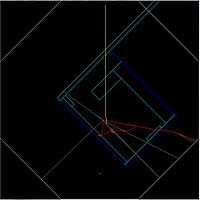
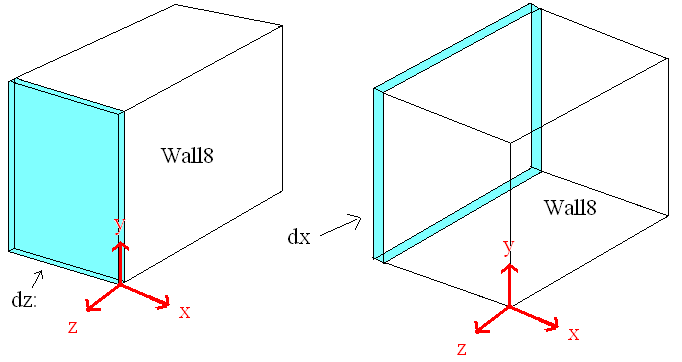
Walls are numbered as given in the first figure. Origin of coordinate system is located at lower left corner of the wall#1. Door way to the accelerator room was named wall#8. As shown figures, we used a slice (dz) from wall#8 as detecting area to study radiation. Special interest was given to slice dz (blue color), and called doorway. 2mm thick tungsten target was placed on the 10 MeV e- beam line, as shown in figure. e- beam (red) is circular with radius of 6 mm.
Energy deposited
energy through the door
Following figures show number of photons and electrons deposited in the doorway before and after shifting the cavity respectively. Figures show that at new location we will have a hot spot at the corner of doorway around 1 m height.
Before:
After:
Following two figures are energy profiles on the doorway before (blue) and after (red) shifting the cavity to new location. The radiation increased about factor of 10 after.
Photons:
Electrons:
Shielding The Radiation
Cavity was shifted to new location to study the radiation and shielding effect on radiation. We used cylindrical shielding around the cavity end one cap at the upstream end of the cavity (as shown in the following figure). Shielding was increased by the increment of 6 mm. At 2 increments, radiation was reduced to same level before shifting.
Conclusion
A 1.2 cm (1/2 inch) thick layer of Pb ( 2 , 1/4 inch thick lead sheets) around the new accelerator cavity's position will restore the radiation footprint of the original accelerator's position.
We did radiation measurement to estimate the dose rate on the monitor on the experimental cell side after shifting the cavity to new location. We conclude that, at new location for cavity, for condition: electron beam energy of 16 MeV, beam peak current of 40 mA, pulse width full width half max of 150 ns, it is safe to run at 900 Hz rap rate.
Simulation work
Design a simulation to determine radiation footprint in HRRL cell.
1.) The ceiling is 4 feet thick
2.) there is PB shiedling between the HRRL accelerator room and the accelerator operator station
3.) the dirt is about 10 feet thick on the wall side where the accelerator is going to be mounted
4.) determine shielding wall thickness for HRRL cavity to reduce dose out the door
5.) Determine shielding for Tungsten converter
Drawing
Get a drawing from facilities documenting the shielding in that cell with dimensions
Denton Dance: x4710, may be able to provide drawings. B119 Beam Lab
Material Definitions
Concrete
Concrete has 6 elements and a density of 2.7 g/cm^3
| Element | Atomic Weight (A) | Atomic Number (Z) | Proportion by Weight |
| 1 | 1.0079 | 1. | 0.004 |
| 2 | 15.9994 | 8. | 0.509 |
| 3 | 26.981539 | 13 | 0.034 |
| 4 | 28.0855 | 14. | 0.345 |
| 5 | 40.078 | 20 | 0.070 |
| 6 | 55.8474 | 26. | 0.038 |
GEANT4 code
a = 1.0079*g/mole; G4Element* elH = new G4Element(name="Hydrogen",symbol="H" , z= 1., a); a = 15.9994*g/mole; G4Element* elO = new G4Element(name="Oxygen" ,symbol="O" , z= 8., a); a = 26.981539*g/mole; G4Element* elAl = new G4Element(name="Aluminum",symbol="Al" , z= 13., a); a = 28.0855*g/mole; G4Element* elSi = new G4Element(name="Silicon",symbol="Si" , z= 14., a); a = 40.078*g/mole; G4Element* elCa = new G4Element(name="Calcium",symbol="Ca" , z= 20., a); a = 55.8474*g/mole; G4Element* elNi = new G4Element(name="Iron",symbol="Fe" , z= 26., a); density =2.7*g/cm3; G4Material* Concrete = new G4Material(name="Concrete ",density,ncomponents=6); Concrete->AddElement(elH, fractionmass=0.4*perCent); Concrete->AddElement(elO, fractionmass=50.9*perCent); Concrete->AddElement(elAl, fractionmass=3.4*perCent); Concrete->AddElement(elSi, fractionmass=34.5*perCent); Concrete->AddElement(elCa, fractionmass=7.0*perCent); Concrete->AddElement(elNi, fractionmass=3.8*perCent);
Relative Rates
The first step in the simulation will be to compare relative radiation rates at the exit of the accelerator room. The radiation exiting the accelerator room before and after moving the accelerator will be simulated. Although all particles can be tracked we will mostly be interested in gamma and neutron fluxes through the door. The ratio of before/after moving fluxes for gamma and neutron should be plotted as a function of energy.
Geometry
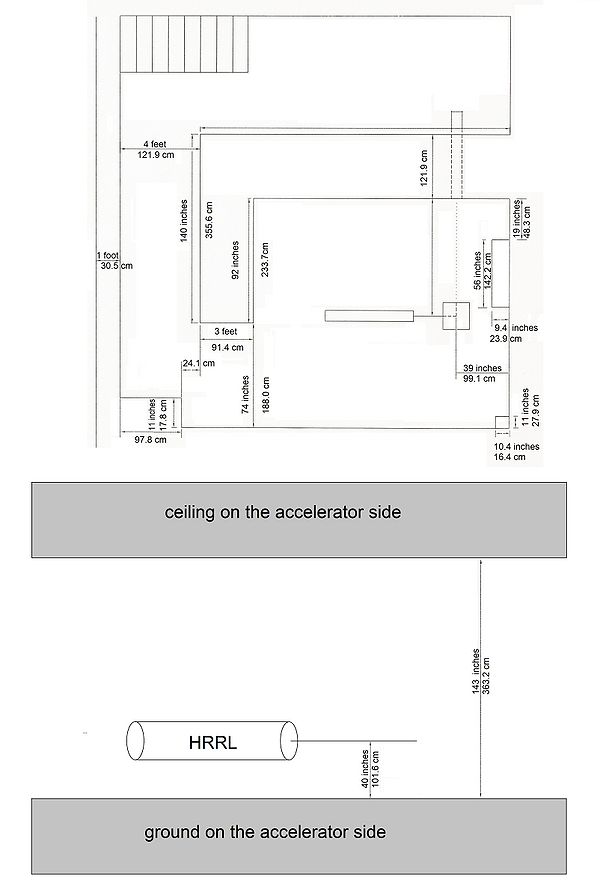
[HRRL room dimension measured by Jason Swanson]
HRRL Geom by Sadiq
what is the thicknes of the walls below.
No dirt inside walls.
Wall Number 3, 4 and 5 are 1 feet thick.
Ceiling is 5 feet thick. Above that is 1st floor metal structure.
GEANT4 Simulation Setup
HRRL Room Top view
Wall is not real wall. Its material is air, this wall is just used as detector to detect particles and photons.
The origin of the coordinate system moved the the other corner of the wall#1 as shown one of the figure in below.
HRRL Room 45 Degree View
HRRL Room Side view
HRRL Electron Source and Tungsten Target 45 Degree View
HRRL Electron Source and Tungsten Target Top View
HRRL New Electron Source
Geant4 Codes
GPS e- Source
/gps/particle e-
/gps/energy 10. MeV
/gps/pos/type Plane
/gps/pos/shape Circle
/gps/pos/radius 0.6 cm
/gps/pos/sigma_r 3 mm
/gps/pos/sigma_x 3 mm
/gps/pos/sigma_y 3 mm
Old Position, -Z direction:
/gps/pos/centre 380 101.6 -93.68 cm
New Postion, X direction:
/gps/pos/centre 66.5 101.6 93.93 cm
/gps/direction 1 0 0
Physics List
10 MeV Gamma hit 2 meter D2O target to show neutron from disintegrated deuterium.
Yellow: neutron
Red: electron
Gray: gamma
It is better to show the tracking output in order to see the physics process and particles created.
Dectector Construction
File:Detector Construction.txt
Electron and photon interactions with the target and the walls
Electron in Target
*********************************************************************************************************
* G4Track Information: Particle = e-, Track ID = 8, Parent ID = 2
*********************************************************************************************************
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
1 1.66401 m 1.01473 m 93.5217 cm 0 eV 147.944 keV29.1396 um 29.1396 um Target eIoni
Electron go into Wall3
*********************************************************************************************************
* G4Track Information: Particle = e-, Track ID = 1, Parent ID = 0
*********************************************************************************************************
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
1 1.64085 m 1.03791 m 93.998 cm 9.76788 MeV198.526 keV97.4316 cm 97.4316 cm World eIoni
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
2 1.67863 m 1.03716 m 93.7509 cm 9.73665 MeV7.70861 keV3.7869 cm 1.01218 m World eIoni
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
3 2.38158 m 1.04721 m 88.1765 cm 9.53633 MeV 137.3 keV70.5761 cm 1.71795 m World eIoni
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
4 4.8856 m 1.06243 m 1.22615 m 9.04023 MeV496.099 keV2.5446 m 4.26254 m World Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
5 5.194 m 1.034 m 1.28563 m 8.91744 MeV122.789 keV31.6299 cm 4.57884 m Wall3 Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
6 7.5 m 95.4945 cm 1.63263 m 8.49278 MeV424.668 keV2.34972 m 6.92856 m OutOfWorld Transportation
Gamma go into Wall3
*********************************************************************************************************
* G4Track Information: Particle = gamma, Track ID = 3, Parent ID = 1
*********************************************************************************************************
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
1 4.8856 m 98.0398 cm 24.6372 cm 78.0395 keV 0 eV 3.08802 m 3.08802 m World Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
2 5.194 m 97.6205 cm 17.6225 cm 78.0395 keV 0 eV 31.6305 cm 3.40432 m Wall3 Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
3 5.97662 m 96.5562 cm -1.78528 mm 0 eV 403 eV 80.2682 cm 4.207 m World phot
Gamma go into Wall4
*********************************************************************************************************
* G4Track Information: Particle = gamma, Track ID = 2, Parent ID = 1
*********************************************************************************************************
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
1 2.98112 m 1.42043 m 1.8796 m 92.4831 keV 0 eV 1.72044 m 1.72044 m World Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
2 3.42618 m 1.53616 m 2.1844 m 92.4831 keV 0 eV 55.1695 cm 2.27214 m Wall4 Transportation
#Step# X Y Z KineE dEStep StepLeng TrakLeng Volume Process
3 7.5 m 2.59551 m 4.97442 m 92.4831 keV 0 eV 5.05 m 7.32214 m OutOfWorld Transportation
Radiation Ratio estimate for Wall 8 2/25/10
A GEANT4 simulation was used to compare the radiation footprint of the HRRL before and after its relocation. The ratio of radiation incident at the exit of the accelerator room (identified as Wall #8 in the pictures below) was estimated by tracking electrons, photons, and neutrons.
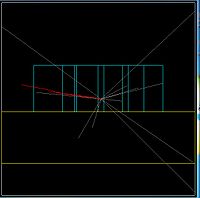
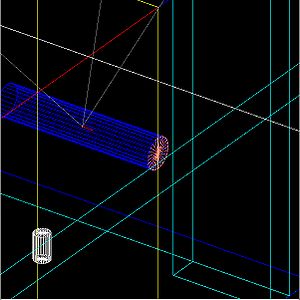
The red line in the figure below indicates the interaction point of an electron from the HRRL accelerator with a Tungsten radiator used to convert the incident electron into e+e- pairs. The proposed location for the HRRL is to move it just below wall #6 and in front of the "Z" axis label..
The drawing below identifies the location of Wall #8. Wall 8 is composed of air, this wall is just used as detector to detect particles and photons.
Number of particles
Simulation results by number of particles for 10 million run.
| Particle | Numbers at Old Position [1] | Numbers at New Position [2] | Ration (new:old) |
| e- | 697728 | 2397851 | 3.43665583 |
| gamma | 375260 | 779381 | 0.481484665 |
G4 code for registering particles in wall8. Daughter particles are also registered as long as they are in wall8.
if( fTrack->GetVolume()->GetName() =="Wall8" && (fTrack->GetDefinition()->GetPDGEncoding()==22 ||fTrack->GetDefinition()->GetPDGEncoding()==11 ||fTrack->GetDefinition()->GetPDGEncoding()==2212 ||fTrack->GetDefinition()->GetPDGEncoding()==2112 ))
{
if (fTrack->GetDefinition()->GetPDGEncoding()==22 ) //if gamma
{ ig++;
outfile
<< ig << " 22 "
<<fTrack->GetKineticEnergy() << " "
<< fTrack->GetPosition().x()<< " "
<< fTrack->GetPosition().y()<< " "
<< fTrack->GetPosition().z()<< " "
<< fTrack->GetMomentum().x() << " "
<< fTrack->GetMomentum().y() << " "
<< fTrack->GetMomentum().z() << " "<< G4endl;}
if (fTrack->GetDefinition()->GetPDGEncoding()==11 ) //if e-
{ie++;
outfile
<< ie << " 11 "
<<fTrack->GetKineticEnergy() << " "
<< fTrack->GetPosition().x()<< " "
<< fTrack->GetPosition().y()<< " "
<< fTrack->GetPosition().z()<< " "
<< fTrack->GetMomentum().x() << " "
<< fTrack->GetMomentum().y() << " "
<< fTrack->GetMomentum().z() << " "<< G4endl;}
if (fTrack->GetDefinition()->GetPDGEncoding()==2212 ) //if proton
{ip++;
outfile
<< ip << " 2212 "
<<fTrack->GetKineticEnergy() << " "
<< fTrack->GetPosition().x()<< " "
<< fTrack->GetPosition().y()<< " "
<< fTrack->GetPosition().z()<< " "
<< fTrack->GetMomentum().x() << " "
<< fTrack->GetMomentum().y() << " "
<< fTrack->GetMomentum().z() << " "<< G4endl;}
if (fTrack->GetDefinition()->GetPDGEncoding()==2112 ) //if neutron
{in++;
outfile
<< in << " 2112 "
<<fTrack->GetKineticEnergy() << " "
<< fTrack->GetPosition().x()<< " "
<< fTrack->GetPosition().y()<< " "
<< fTrack->GetPosition().z()<< " "
<< fTrack->GetMomentum().x() << " "
<< fTrack->GetMomentum().y() << " "
<< fTrack->GetMomentum().z() << " "<< G4endl;}
}
Energy profile
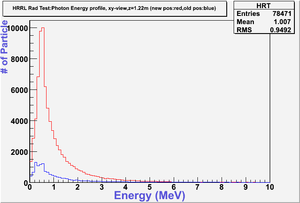
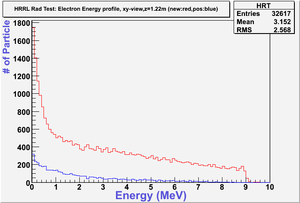
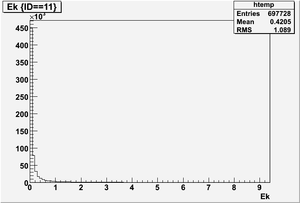
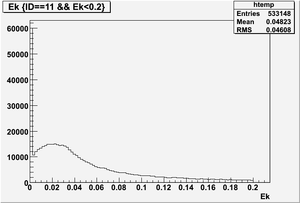
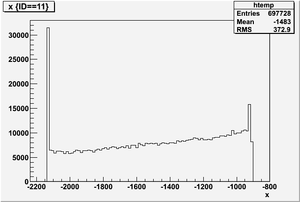
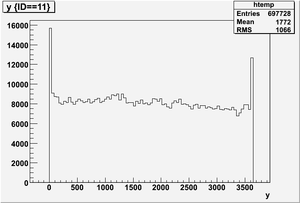
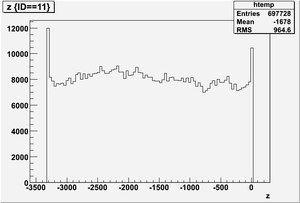
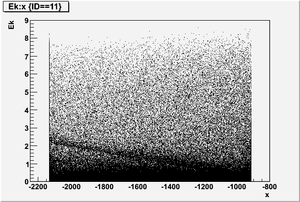
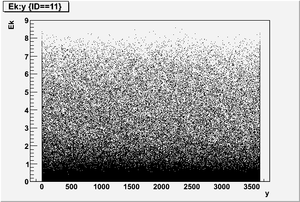
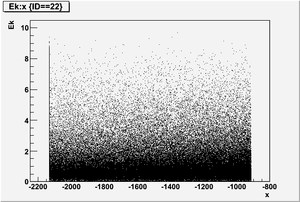
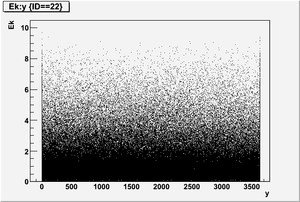
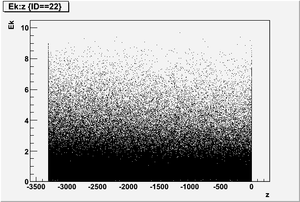
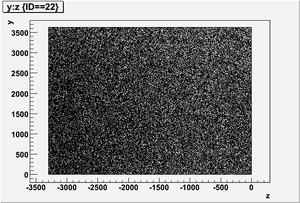
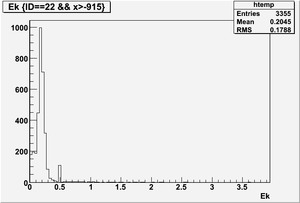
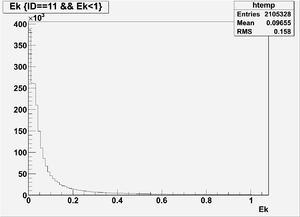
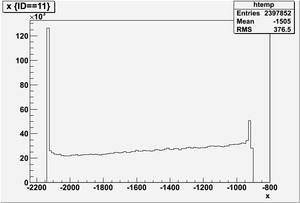
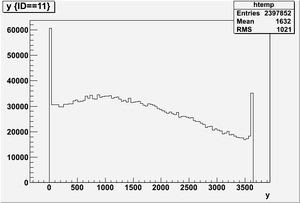
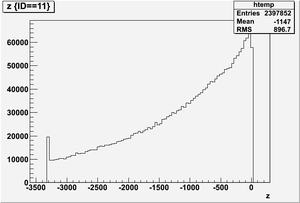
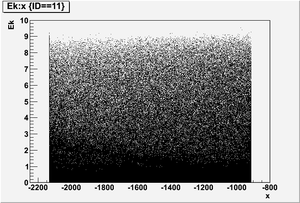
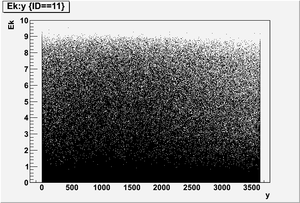
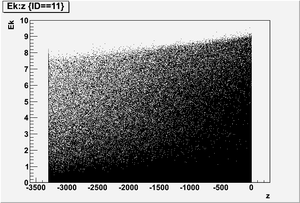
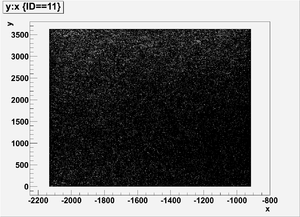
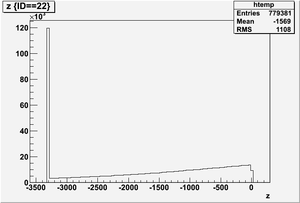
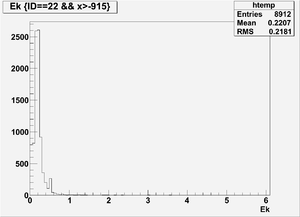
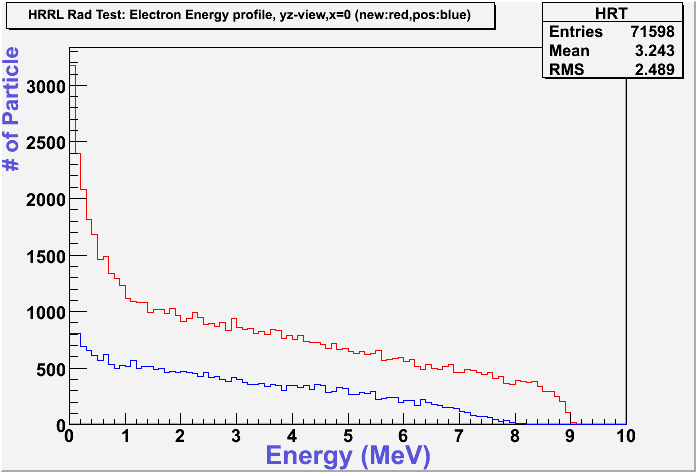
The figures below illustrate the energy spectrum of radiation entering wall #8 (described above) as predicted by a GEANT4 simulation of the HRRL accelerator room.
Old Position
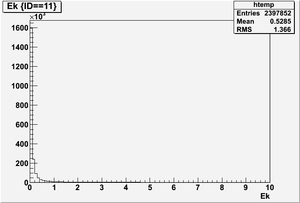
Electron
Kinetic energy (Ek) in the unit of MeV below
Position x in the unit of mm below
Position y
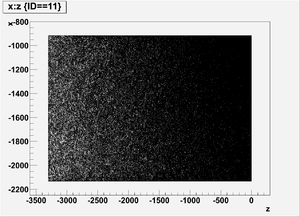
Position z
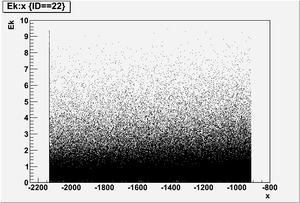
Ek vs x
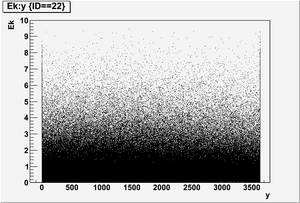
Ek vs y
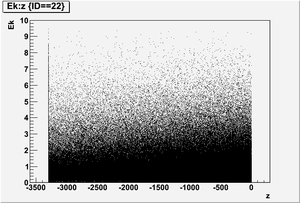
Ek vs z
x vs y
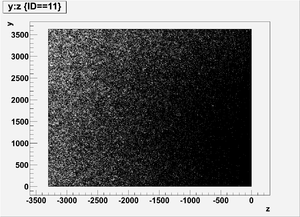
y vs z
z vs x
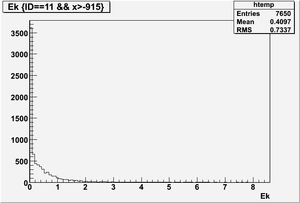
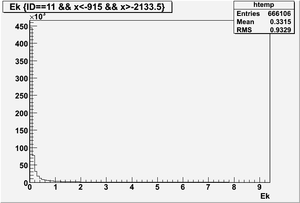
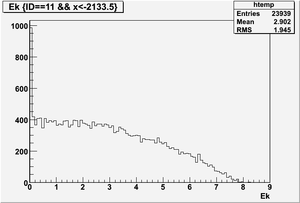
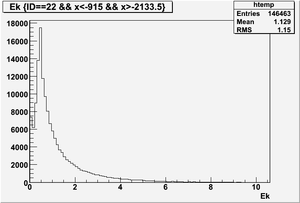
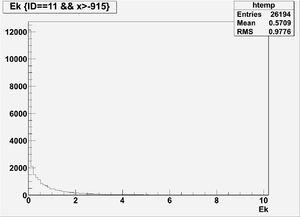
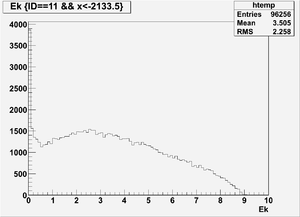
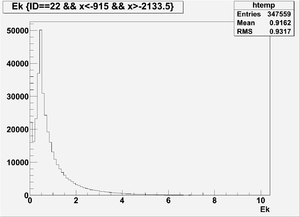
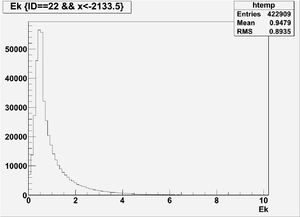
Ek(x>-915mm)
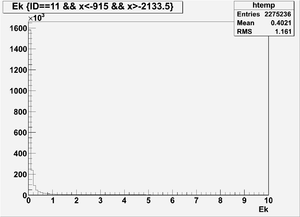
Ek(2133.5mm<x<-915mm)
Ek(x<2133.5mm)
Photon
Kinetic energy (Ek) in the unit of MeV below
Position x in the unit of mm below
Position y
Position z
Ek vs x
Ek vs y
Ek vs z
x vs y
y vs z
z vs x
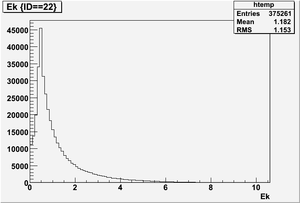
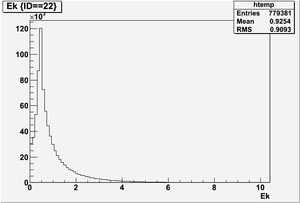
Ek(x>-915mm)
Ek(2133.5mm<x<-915mm)
Ek(x<2133.5mm)
Neutron
Ek vs x
Proton
No proton was seen.
New Position
Electron
Kinetic energy (Ek) in the unit of MeV below
Position x in the unit of mm below
Position y
Position z
Ek vs x
Ek vs y
Ek vs z
x vs y
y vs z
z vs x
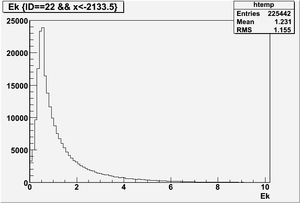
Ek(x>-915mm)
Ek(2133.5mm<x<-915mm)
Ek(x<2133.5mm)
Photon
Kinetic energy (Ek) in the unit of MeV below
Position x in the unit of mm below
Position y
Position z
Ek vs x
Ek vs y
Ek vs z
x vs y
y vs z
z vs x
Ek(x>-915mm)
Ek(2133.5mm<x<-915mm)
Ek(x<2133.5mm)
Neutron
Ek vs x
Proton
No proton was seen.
ROOT commands
The command below will create a program skeleton which you can use to parse the data
hredtest->MakeClass();
.L hredtest.C
hredtest t;
t.Loop();
Sad2->Draw("Colz");
HRRL Radiation Simulations with Thin Detectors
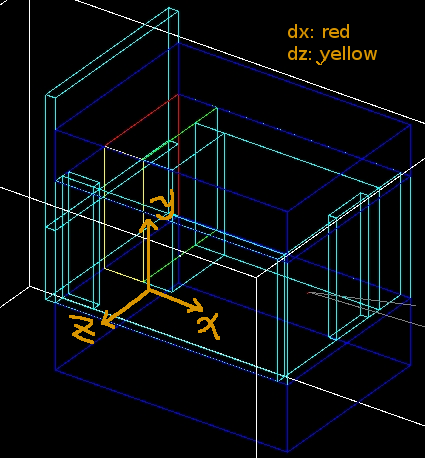
Detectors are created in GEANT4, Detector dz and dx.
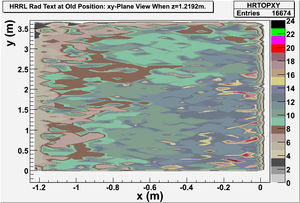
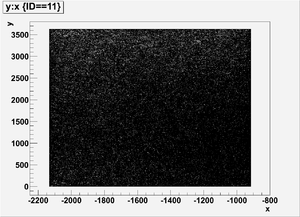
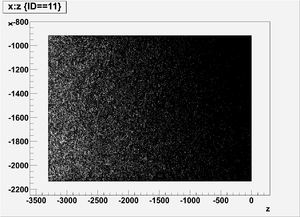
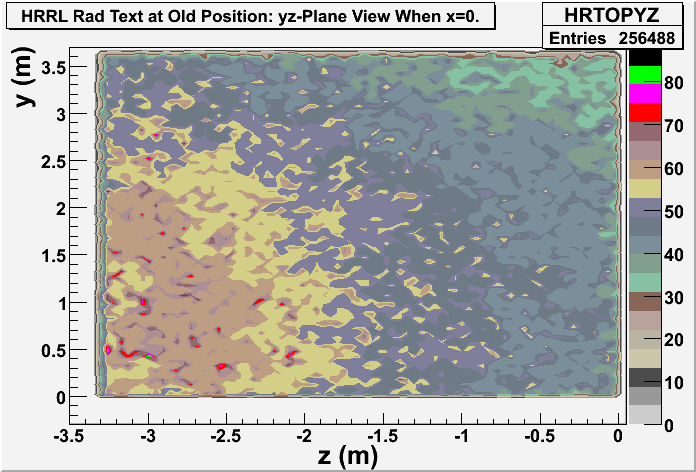
Detector dz: a thin detector in z direction (with thickness dz=1 mircron), and same dimension in xy plane with wall8. It gives xy-plane view of radiation.
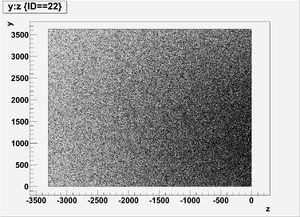
Detector dx: a thin detector in x direction (with thickness dx=1 mircron), and same dimension in yz plane with wall8. It gives yz-plane view of radiation.
Origin of the coordinate system is moved to new position, shown as in figure below.
Electron and Photon Mixed
New Position
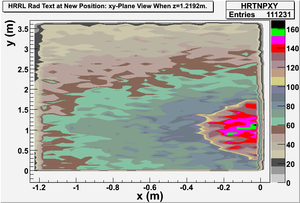
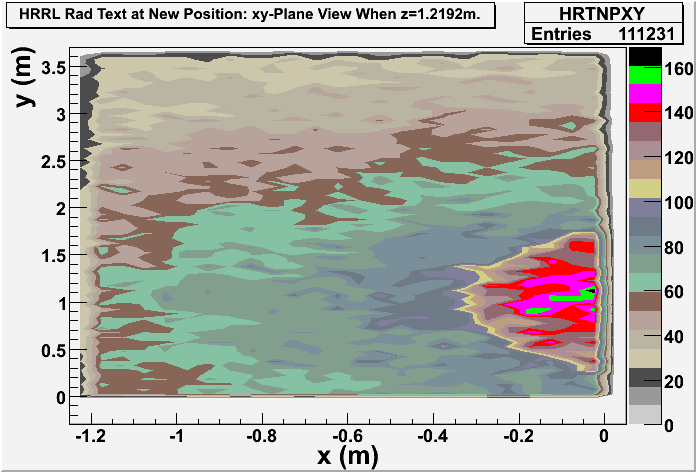
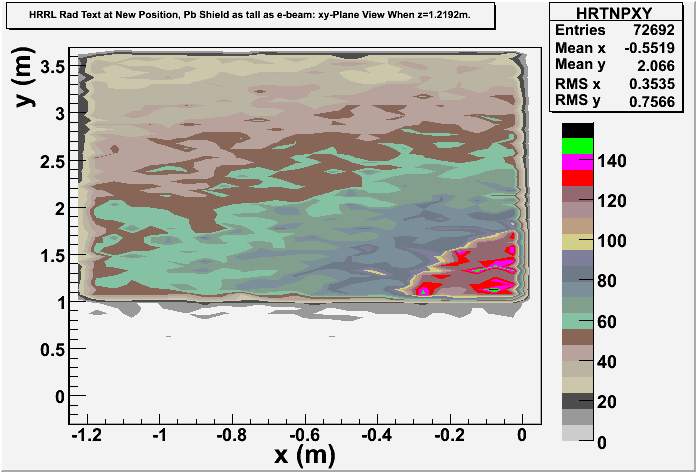
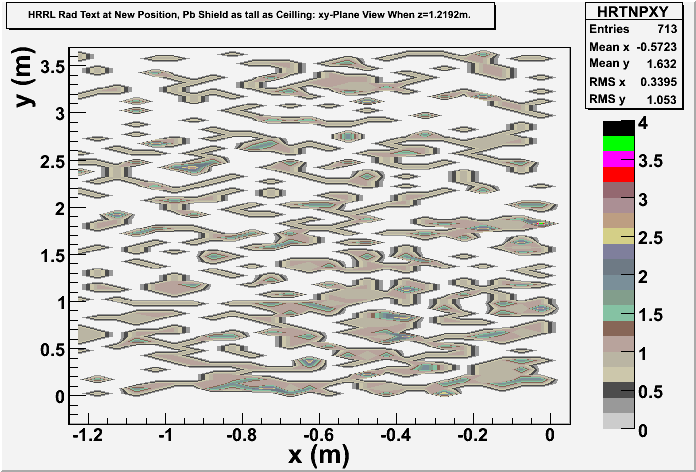
xy-plane view (doorway)
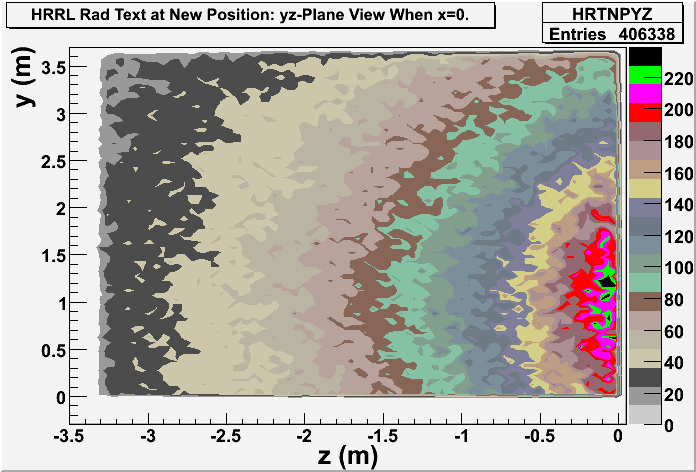
yz-plane view
Old Position
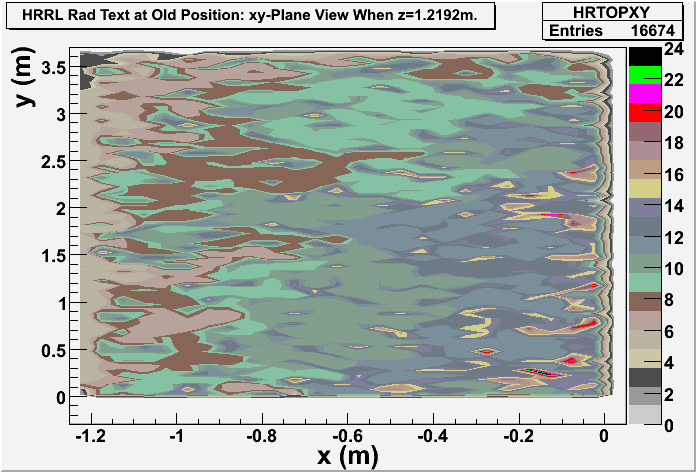
xy-plane view (doorway)
yz-plane view
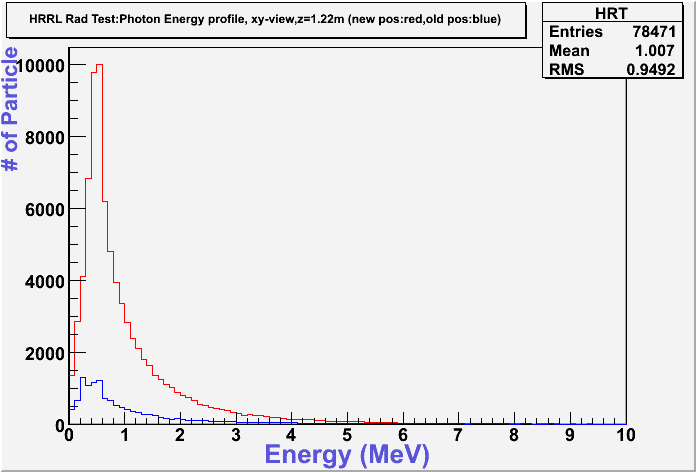
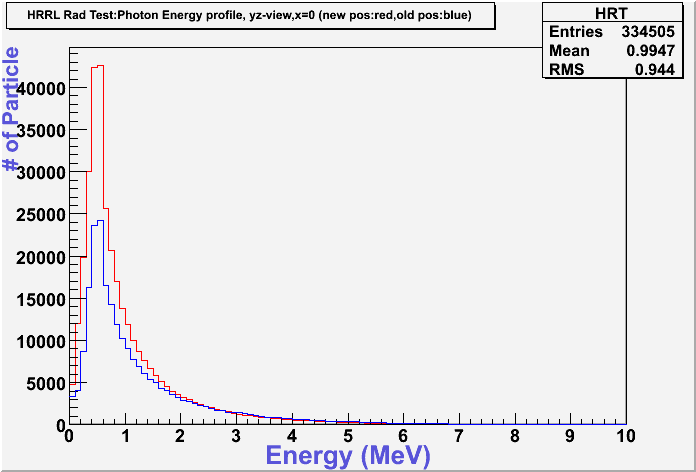
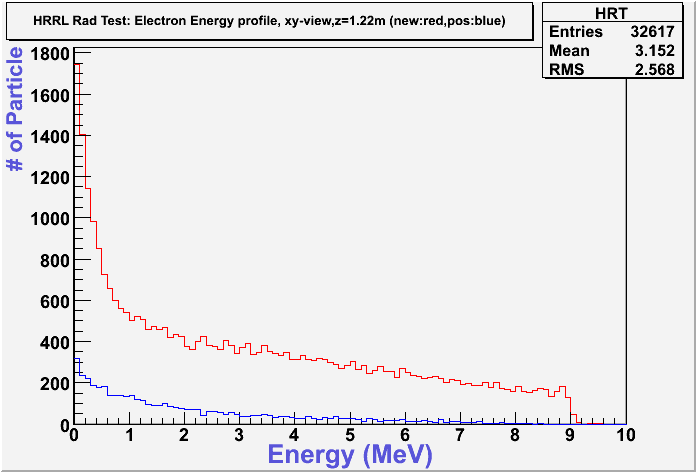
Energy Profile Comparison between Old and New Positions
New position:red color.
Old position:blue color.
Photon
Photon: xy-plane view
These are the photons coming through the opening? Yes, these 2 detectors are very thin (1 micron thick). One is thin on z direction, gives xy-plane view, at the operator side of wall8. Another one is thin on x direction, gives yz-plane view, at the accelerator side of the room.
These are the photons coming through the wall?
Photon: yz-plane view
Electron
Electron: xy-plane view
Electron: yz-plane view
Energy/incident electron
For each graph determine the total energy deposited per incident electron for the two configurations then take the ratio.
New Position
Electron gun fired 10 million times, and the electron beam energy is 10 MeV.
xy-view:
Total Photon Energy (if(evt.ID==22) Ek_g_t +=evt.Ek;) = 79020.5; Energy deposited per electron is: 79020.5 / 10 000 000 = 0.00790205 MeV/Electron;
Total Electron Energy (if(evt.ID==11) Ek_e_t +=evt.Ek;) = 102820; Energy deposited per electron is: 102820 / 10 000 000 = 0.0102820 MeV/Electron;
Combined: (79020.5 + 102820)/10 000 000 = 0.01818405
yz-view:
Total Photon Energy (if(evt.ID==22) Ek_g_t +=evt.Ek;) = 332712; Energy deposited per electron is: 332712 / 10 000 000 = 0.0332712 MeV/Electron;
Total Electron Energy (if(evt.ID==11) Ek_e_t +=evt.Ek;) = 232201; Energy deposited per electron is: 232201 / 10 000 000 = 0.0232201 MeV/Electron;
Old Position
Electron gun fired 10 million times, and the electron beam energy is 10 MeV.
xy-view:
Total Photon Energy (if(evt.ID==22) Ek_g_t +=evt.Ek;) = 12397.2; Energy deposited per electron is: 12397.2 / 10 000 000 = 0.00123972 MeV/Electron;
Total Electron Energy (if(evt.ID==11) Ek_e_t +=evt.Ek;) = 8670.29; Energy deposited per electron is: 8670.29 / 10 000 000 = 0.000867029 MeV/Electron;
Combined: (12397.2 + 8670.29)/10000000 = 0.002106749
yz-view:
Total Photon Energy (if(evt.ID==22) Ek_g_t +=evt.Ek;) = 286124; Energy deposited per electron is: 286124 / 10 000 000 = 0.0286124 MeV/Electron;
Total Electron Energy (if(evt.ID==11) Ek_e_t +=evt.Ek;) = 78727.9; Energy deposited per electron is: 78727.9 / 10 000 000 = 0.00787279 MeV/Electron;
Ratio of new to old position
Following table gives
| photon | electron | combined | |
| xy-view | 0.00790205/0.00123972 = 6.4 | 0.0102820/0.000867029 = 1.2 | 0.01818405/0.002106749= 8.6 |
| yz-view | 0.0332712/0.0286124 =1.2 | 0.0232201/0.00787279 = 2.9 |
Lead Shielding around HRRL in New Positon
Pb Wall is as Tall as Electron Beam
Lead wall is 3-inch (10.16 cm) thick.
45 degree view
Top view
Side view
Simulation Results
Note: Electron and photon are differentiated.
Door view:
Side Wall view:
Deposited energy -vs Pb thickness
Consider draping a lead blanket which covers from the accelerator exit port to the Tungsten converter. We have a few such blankets down in the HRRL. Go see how thick they are and then simulate the thickness with one blanket then with two.
Plot the total energy deposited by photons and separately electrons for at least 3 Pb thicknesses, one of which is 3".
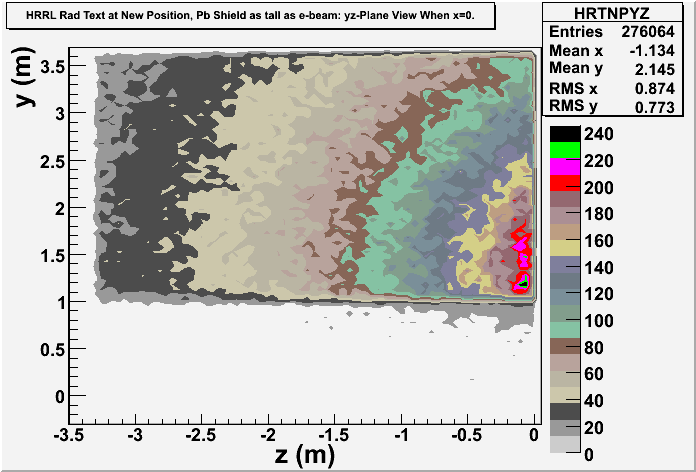
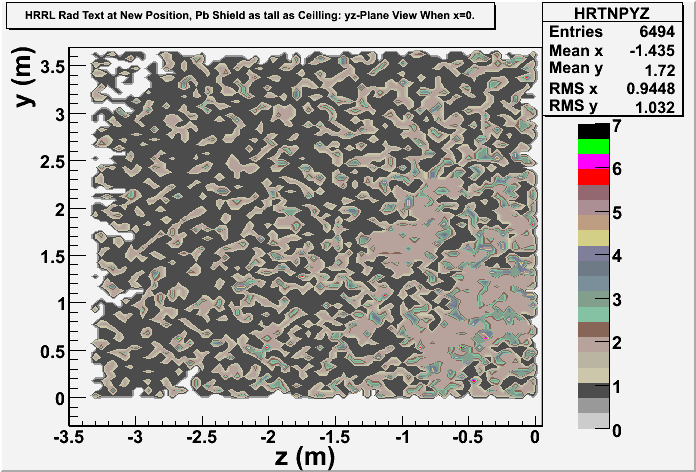
Pb Wall is as Tall as Ceiling
Simulation Results
Note: Electron and photon are differentiated.
Door view:
Side Wall view:
Cylindrical Pb Shielding around Target Increment Test
The thickness of lead sheets in the accelerator room is around 6 mm. We desire to use this lead sheets as shielding to shield HRRL in new position. So, I run simulation to study the change in radiation as thickness of shielding increase by 1 increment.
Make the units Energy /electron
Increment Test
Lead shielding was increased from 1 16 times of thickness of lead sheet.
Increment Test
Lead shielding was increased from 1 to 16 times of thickness of lead sheet.
Fill in the two rows below
| Increment | Contour Plot | ||||
| 0 (before move) | 12397.2 | 8670.29 | 21067.49 | 0.002106749 |
|
| 0 (after move) | 79020.5 | 102820 | 181840.5 | 0.01818405 |
|
| 1 | 67909.8 | 1322.74 | 69232.5 | 0.00692325 | 
|
| 2 | 47080.4 | 849.284 | 47929.7 | 0.00479297 | 
|
| 3 | 32447.3 | 660.904 | 33108.2 | 0.00331082 | 
|
| 4 | 23381.6 | 488.022 | 23869.7 | 0.00238697 | 
|
| 5 | 16639.2 | 348.788 | 16988 | 0.0016988 | 
|
| 6 | 12052 | 269.449 | 12321.5 | 0.00123215 | 
|
| 7 | 8867.79 | 224.403 | 9092.19 | 0.000909219 | 
|
| 8 | 6256.38 | 155.28 | 6411.66 | 0.000641166 | 
|
| 9 | 4805.09 | 130.132 | 4935.22 | 0.000493522 | 
|
| 10 | 3397.84 | 98.6598 | 3496.5 | 0.00034965 | 
|
| 11 | 2563.9 | 88.4048 | 2652.3 | 0.00026523 | 
|
| 12 | 1845.77 | 72.3448 | 1918.11 | 0.000191811 | 
|
| 13 | 1459.55 | 54.9425 | 1514.49 | 0.000151449 | 
|
| 14 | 1025.4 | 63.0917 | 1088.49 | 0.000108849 | 
|
| 15 | 690.531 | 45.8029 | 736.334 | 0.000736334 | 
|
| 16 | 515.095 | 54.7029 | 569.798 | 0.000569798 | 
|
Simulation for corrected HRRL and Target position
After shifting origin of the coordinate system from one corner of the Wall#1 to the other corner, I forgot to shift position of the HRRL and target. Here, I want to correct position of HRRL and target in simulation and run the increment test again.
HRRL will be bolt the wall, so on z-axis it is very simple to place electron source, it is just radius of the HRRL. On x-axis, the length of the HRRL is 5 feet. If we subtract the distance between wall#1 and wall#6, which is 24.1 cm, we will have the position of electron source. This distance 128.3 cm. If we allow 5 cm distance for wires etc, then electron source should be placed 133.3 cm.
The converter should be placed electron beam axis, which will have same z-coordinates as electron beam source in simulation. However, on x-axis, we have 2 Q1B after HRRL. Each Q1B has thickness of 24 cm. If we allow spacing of 2 cm between them, we will have 50 cm of distance taken up by these 2 quad sets. We would like to place converter 10 cm after the quads. Converter finally end up at 193.3 cm (133.3cm+50cm+10cm) on x-axis.
| Increment | Contour Plot | ||||
| 0 (before move) | 12658.4 | 8493.66 | 21152.1 | 0.00126584 | 
|
| 0 (after move) | 26394.9 | 50108.1 | 76503.1 | 0.00263949 | 
|
| 1 | 17819.1 | 430.89 | 18250 | 0.00178191 | 
|
| 2 | 10600.8 | 293.753 | 10894.5 | 0.00106008 | 
|
| 3 | 6722.33 | 271.369 | 6993.7 | 0.000672233 | 
|
| 4 | 4393.05 | 214.263 | 4607.31 | 0.000439305 | 
|
| 5 | 2809.48 | 129.821 | 2939.3 | 0.000280948 | 
|
| 6 | 1955.28 | 119.253 | 2074.54 | 0.000195528 | 
|