Difference between revisions of "Geometry (25 MeV LINAC exit port)"
Jump to navigation
Jump to search
| Line 71: | Line 71: | ||
=Funny pictures...= | =Funny pictures...= | ||
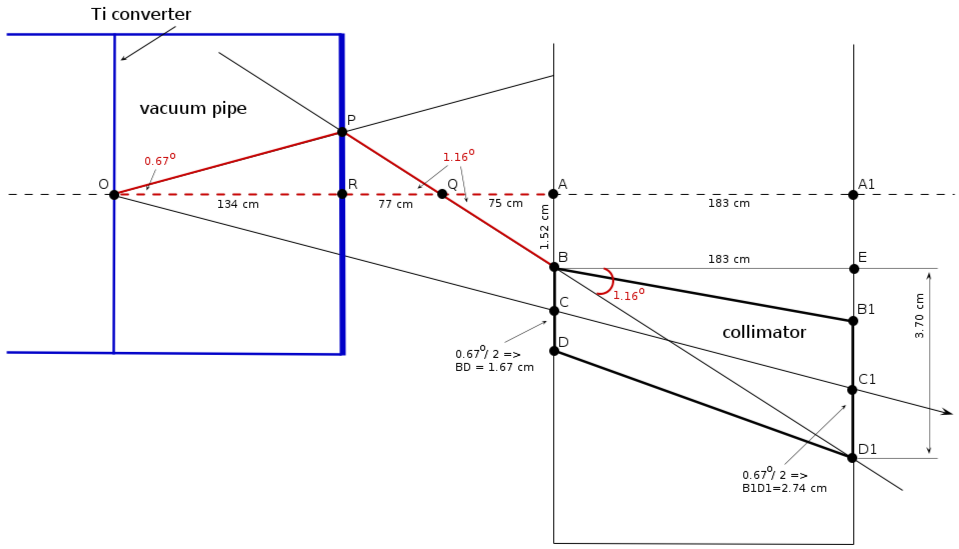
| − | ==how it looks (<math> \Theta_c/2</math>, pipe | + | ==how it looks 1 (<math> \Theta_c/2</math>, box 3"x4" and then pipe 4")== |
| − | [[File: | + | [[File:vacuum_pipe_collimator.png]]<br> |
| − | ==how it looks | + | ==how it looks 2 (<math> \Theta_c/4</math>, box 3"x4" and then pipe 4")== |
| − | [[File: | + | [[File:vacuum_pipe_collimator.png]]<br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Revision as of 05:54, 11 June 2010
Critical angle
Kicker angle
Vacuum pipe location ()
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
:
minimal distance from the wall
Vacuum pipe location ()
collimator location
1) center position:
(wall 1)
(wall 2)
2) collimator diameter:
(wall 1)
(wall 2)
collimator critical angle
from triangle :
minimal distance from the wall
from triangle FAB:
Funny pictures...
how it looks 1 (, box 3"x4" and then pipe 4")
how it looks 2 (, box 3"x4" and then pipe 4")