Difference between revisions of "Forest UCM NLM GalileanTans"
Jump to navigation
Jump to search
(Replaced content with " 200 px Consider the description of an object in motion using two different coordinate systems <math>S</math> and <math>S^{\prime…") |
|||
| Line 1: | Line 1: | ||
| − | |||
[[File:TF_UCM_GalileanTans_RefFrame.png | 200 px]] | [[File:TF_UCM_GalileanTans_RefFrame.png | 200 px]] | ||
| − | Consider the | + | Consider the description of an object in motion using two different coordinate systems <math>S</math> and <math>S^{\prime}</math>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Assume that <math>S^{\prime}</math> is a coordinate system moving at a CONSTANT speed <math>v</math>. | |
| − | |||
[[Forest_UCM_NLM#Galilean_Transformations]] | [[Forest_UCM_NLM#Galilean_Transformations]] | ||
Revision as of 13:41, 18 August 2014
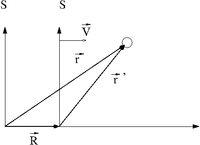
Consider the description of an object in motion using two different coordinate systems and .
Assume that is a coordinate system moving at a CONSTANT speed .