Difference between revisions of "Forest UCM NLM"
(→Polar) |
(→Polar) |
||
| Line 44: | Line 44: | ||
Position: | Position: | ||
| + | |||
| + | Because <math>\hat{r}</math> points in a unique direction we can write the position vector as | ||
:<math>\vec{r} = r \hat{r}</math> | :<math>\vec{r} = r \hat{r}</math> | ||
| Line 49: | Line 51: | ||
:<math>\vec{r} \ne r \hat{r} +\phi \hat{\phi} </math>: <math>\phi</math> does not have the units of length | :<math>\vec{r} \ne r \hat{r} +\phi \hat{\phi} </math>: <math>\phi</math> does not have the units of length | ||
| + | |||
| + | The unit vectors (<math>\hat{r}</math> and <math>\hat{\phi}</math> ) are changing in time. You could express the position vector in terms of cartesian unit vector in order to avoid this | ||
| + | |||
| + | :<math>\vec{r} = r \cos(\phi) \hat{i} + r \sin(\phi)\hat{j}</math> | ||
The dependence of position with \phi can be seen if you look at how the position changes with. | The dependence of position with \phi can be seen if you look at how the position changes with. | ||
| Line 63: | Line 69: | ||
:<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i} </math> | :<math>\vec{v}</math> = <math>\frac{d \vec{r}}{dt}</math> = <math>\frac{d x}{dt}\hat{i} + \frac{d y}{dt}\hat{i} + \frac{d z}{dt}\hat{i} </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
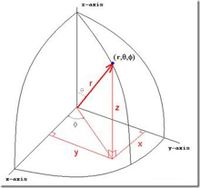
===Spherical=== | ===Spherical=== | ||
Revision as of 19:02, 18 June 2014
Newton's Laws of Motion
Limits of Classical Mechanic
Classical Mechanics is the formulations of physics developed by Newton (1642-1727), Lagrange(1736-1813), and Hamilton(1805-1865).
It may be used to describe the motion of objects which are not moving at high speeds (0.1) nor are microscopically small ( ).
The laws are formulated in terms of space, time, mass, and force:
Space and Time
Space
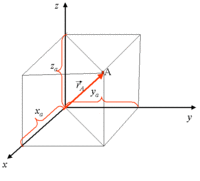
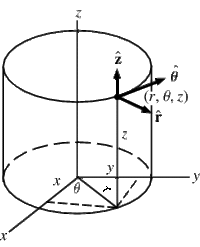
Cartesian, Spherical, and Cylindrical coordinate systems are commonly used to describe three-dimensional space.
Cartesian
Vector Notation convention:
Position:
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =
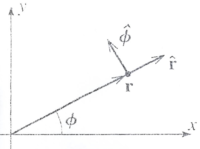
Polar
Position:
Because points in a unique direction we can write the position vector as
- : does not have the units of length
The unit vectors ( and ) are changing in time. You could express the position vector in terms of cartesian unit vector in order to avoid this
The dependence of position with \phi can be seen if you look at how the position changes with.
Velocity:
- = =
cartesian unit vectors do not change with time (unit vectors for other coordinate system types do)
- = =