Lagrange's Foramlism for Classical Mechanics
Hamilton's principle
Hamilton's principle falls out of the calculus of variations in that seeking the shortest time interval is the focus of the variations.
- Of all possible paths along which a dynamical system may move from on point to another within a specified time interval, the actual path followed is that which minimizes the time integral of the difference between the kinetic and potential energies.
Casting this in the language of the calculus of variations
- [math]S \equiv \int_{t_1}^{t_2} \left ( T(\dot x) - U(x) \right ) dt = \int_{t_1}^{t_2} f(x,\dot x ; t) dt = \int_{t_1}^{t_2} \mathcal {L} ( x, \dot x;t) dt [/math]
if you want the above "action" integral to be stationary then according to the calculus of variations you want the Euler-Lagrange equation to be satisfied where
- [math] \left [ \left ( \frac{\partial f}{\partial x} \right ) - \frac{d}{dt} \left ( \frac{\partial f}{\partial \dot x} \right ) \right ] =0 [/math]
or
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial x} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x} \right ) \right ] =0 [/math]
here [math]x^{\prime} = \frac{d x}{d t} \equiv \dot x[/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial x} \right ) = \frac{\partial }{\partial x} \left ( T(\dot x) - U(x) \right ) = -\frac{\partial U(x)}{\partial x} = F_x[/math] the generalized force if I have conservative forces
- [math] \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x} \right ) = \frac{d}{dt} \left ( \frac{\partial }{\partial \dot x} \right ) \left ( T(\dot x) - U(x) \right ) [/math]
- [math] = \frac{d}{dt} \left ( \frac{\partial }{\partial \dot x} \right ) T(\dot x) = \frac{d}{dt} m \dot x = \frac{d}{dt} p_x = \dot{p}_x = F_x [/math] Newton's second law in an Inertial reference frame = time derivative of the generalized momentum
thus
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial x} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x} \right ) \right ] = F_x - F_x = 0 [/math]
Lagrange's Equations in generalized coordinates
Generalized coordinates [math](q_i)[/math] are a set of parameters that uniquely specify the instantaneous state of a dynamical system.
The number of independent generalized coordinates [math](N_q)[/math] is given by subtracting the number of constraints [math](N_C)[/math] from the number of degrees of freedom [math]N_{DF}[/math].
- [math]N_q = N_{DF} - N_C[/math]
Pedulum example
Consider the 2-D pendulum where an object of mass [math]m[/math] is constrained by a rod of length [math]l[/math]. The object is at one end of the rod and the rod is fixed to rotate about the other end.
- [math]N_{DF} =2 [/math] There are 32 degrees of freedom for the 2-D problem
- [math] N_C =1 [/math] The particle is constrained to a rod
- [math]N_q = 2-1 = 1 [/math] The motion of the particle may be described using one component
The constraint may be expressed in cartesian coordinates as
- [math] x^2 + y^2 = l^2[/math]
you can express the position of the object on the end of a rod as a function of just one generalized coordinate
- [math]\vec r = x \hat i + y \hat j = x \hat i + \sqrt{l^2-x^2} \hat j = \vec r(x)[/math] [math]x[/math] is the generalized coordinate
You could also express the position as a function of the deflection angle [math]\phi[/math] in cartesian coordinates
- [math]\vec r = l \cos \phi \hat i + l \sin \phi \hat j = \vec r (\phi)[/math] [math]\phi[/math] is the generalized coordinate
- Note
- If you were to start using Polar coordinates right away such that
- [math]\vec r = l \hat r[/math]
then the dependence of the function on [math]\phi[/math] would not be obvious as this dependence is implicit to changes in the [math]\hat r[/math] direction
The number of generalized coordinates becomes more obvious when you begin expressing the Potential and Kinetic Energy
- [math]U = mgh = l( 1-\cos \phi)[/math]
- [math] T = \frac{1}{2} m v^2 = \frac{1}{2} l^2 \dot \phi^2[/math]
Motion on Sphere example
Consider a particle constrained to move on a sphere of radius [math]R[/math].
- [math]N_{DF} =3 [/math] There are 3 degrees of freedom for the 3-D problem
- [math] N_C =1 [/math] The particle is constrained to the surface of the sphere
- [math]N_q = 3-1 = 2 [/math] The motion of the particle may be described using two components
The constraint expressed in terms of cartesian coordinates is
- [math] x^2 + y^2 + z^2 = R^2[/math]
The above constraint equation can be used to reduce the degrees of freedom by using the constraint to eliminate one of the above components
for Example
- [math] z^2 = R^2-x^2 - y^2[/math]
- [math]\vec r = x \hat i + y \hat j \pm \sqrt{R^2-x^2 - y^2} \hat k = \vec r ( x,y)[/math]
or if you chose the angles [math]\theta[/math] and [math]\phi[/math] from spherical coordinates
- [math] \vec r = R \cos \phi \sin \theta \hat i + R \sin \phi \sin \theta \hat j + R \cos \theta \hat k = \vec r (\phi, \theta) [/math]
Generalized Force and Momentum
- Generalized Force [math]\equiv \frac{\partial \mathcal {L} }{\partial q}[/math]
- Generalized Momentum [math]\equiv \frac{\partial \mathcal {L} }{\partial \dot q}[/math]
As shown above, Hamilton's principle leads to a re-expression of Newton's second law through the Euler-Lagrange Equation in a differential form known as Lagrange's equations.
Below is the Euler-Lagrange equations expressed in terms of generalized coordinates.
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) \right ] [/math]
Holonomic
If each coordinate used to describe a system can vary independently of the others, then the system is said to be holonomic.
A Non-holonomic system, has a lest one coordinate that depends on one of the others thereby reducing the number of degrees of freedom.
Example: Consider a sphere constrained to roll on a plane (ball on the floor). A spheres position on the plane can be specified using 2 coordinates and the orientation ( rotation) of a point on the sphere can be described by 3 coordinates. Thus, this system has 5 degrees of freedom.
The coordinates are not independent since as the sphere rolls without slipping then at least two coordinates must change making the system nonholonomic.
other examples: car, bicycle
Example: Lagrangian for object in 2-D moving in a conservative field
In cartesian coordinates
In cartesian coordinates the generalized coordinates are represented as the parameters x and y
- [math]\mathcal L(x,\dot x, y, \dot y;t) = T - U = \left ( \frac{1}{2} m(\dot x^2 + \dot y^2) \right ) - \left ( U(x,y) \right ) [/math]
- [math] \frac{\partial \mathcal {L} }{\partial q} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) [/math]
- for the generalized coordinate labeled [math]x[/math]
- [math] \frac{\partial \mathcal {L} }{\partial x} = - \frac{\partial U }{\partial x} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x} \right ) = \frac{d}{dt}m \dot x = m\ddot x \Rightarrow F_x = ma_x[/math]
- for the generalized coordinate labeled [math]y[/math]
- [math] \frac{\partial \mathcal {L} }{\partial y} = - \frac{\partial U }{\partial y} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot y} \right ) = \frac{d}{dt}m \dot y = m\ddot y \Rightarrow F_y = ma_y[/math]
In polar coordinates
In cartesian coordinates the generalized coordinates are represented as the parameters [math]r[/math] and [math]\phi[/math]
- [math]\mathcal L(r, \dot r, \phi, \dot \phi;t) = T - U = \left ( \frac{1}{2} m(\dot r^2 + r^2 \dot \phi^2) \right ) - \left ( U(r,\phi) \right ) [/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) [/math]
The [math]r[/math] parameter
- [math] \frac{\partial \mathcal {L} }{\partial r} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot r} \right ) [/math]
- [math] mr\dot \phi^2-\frac{\partial U }{\partial r} = m \ddot r [/math]
- [math] mr\dot \phi^2+F_r = m \ddot r [/math]
- [math] \Rightarrow F_r = m\left ( \ddot r - r\dot \phi^2\right ) [/math]
recall
- [math]\vec{a} = \left ( \ddot{r} -r\dot{\phi}^2 \right) \hat{r} + \left ( 2\dot{r} \dot{\phi} +r \ddot{\phi} \right ) \hat{\phi} [/math]
The [math]\phi[/math] parameter
- [math] \frac{\partial \mathcal {L} }{\partial \phi} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi} \right ) [/math]
- [math] -\frac{\partial U }{\partial \phi} = \frac{d}{dt} \left ( mr^2 \dot \phi \right ) [/math]
In polar coordinates
- [math]\vec \nabla = \frac{ \partial}{\partial r } \hat r + \frac{1}{r} \frac{ \partial}{\partial \phi } \hat \phi[/math]
- [math]\Rightarrow F_{\phi} = \left . -\nabla U \right |_{\hat \phi} = - \frac{1}{r} \frac{ \partial U }{\partial \phi } \hat \phi[/math]
- [math] -\frac{\partial U }{\partial \phi} = \frac{d}{dt} \left ( mr^2 \dot \phi \right ) [/math]
- [math] rF_{\phi} = \frac{d}{dt} \left ( L \phi \right ) [/math]
- [math] \mathcal \tau = \frac{d L }{dt} [/math]
Examples using Lagrange's Equation
Pendulum
Returning to the problem of an object of mass [math]m[/math] attached to a weightless rod of length [math]l[/math] that is constrained to rotate at the end of the rod where there is no mass.
The number of generalized coordinates = 2-1 = 1.
Selecting polar coordinates to describe this system allows a description using generalized coordinates of only one parameter, [math]\phi[/math].
- [math]U = mgh = mgl( 1-\cos \phi)[/math]
- [math] T = \frac{1}{2} m v^2 = \frac{1}{2} l^2 \dot \phi^2[/math]
- [math]\mathcal L(\phi, \dot \phi;t) = T - U = \left ( \frac{1}{2} mr^2 \dot \phi^2 \right ) - mgl( 1-\cos \phi) [/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) [/math]
- [math] \frac{\partial \mathcal {L} }{\partial \phi} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi} \right ) [/math]
- [math] -mgl \sin \phi = \frac{d}{dt} \left (ml^2 \dot \phi \right ) [/math]
- [math] = ml^2 \ddot \phi [/math]
- [math] \ddot \phi + \frac{g}{l} \sin \phi = 0[/math]
Atwoods Machine
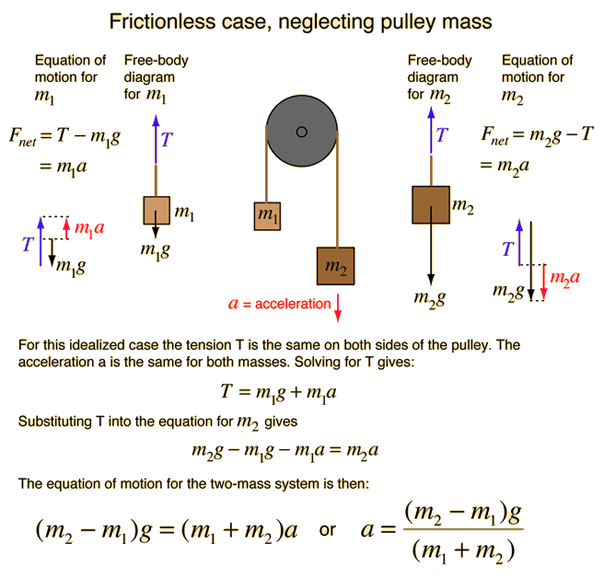
Let [math]x_1[/math] represent the distance of [math]m_1[/math] from the pulley and [math]x_2[/math] the distance of [math]m_2[/math] from the pulley.
The problem has 2 masses hat can move up and down giving us 2 degrees of freedom.
There is a constraint due to the masses being joined by a string of length l.
- [math]x_1 + x_2 + \pi R = l[/math]
The number of generalized coordinate = 2-1 = 1.
- [math]U = -m_1gx_1 - m_1 gx_2 =-m_1gx_1 - m_2 g(l - x_1 - \pi R )[/math]
- [math]= -g(m_1-m_2) x_1 - m_2g(l-\pi R) = -g(m_1-m_2) x_1 + constant[/math]
One may define the potential arbitrarily such that the above constant is zero.
- [math]T = \frac{1}{2} ( m_1 \dot x_1^2 + m_2 \dot x_2^2)[/math]
- [math] = \frac{1}{2} ( m_1 + m_2) \dot x_1^2)[/math]
[math]\mathcal L(x_1, \dot x_1;t) = T - U = \left ( \frac{1}{2} ( m_1 + m_2) \dot x_1^2) \right ) + g(m_1-m_2) x_1 + constant[/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial x_1} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x_1} \right ) [/math]
- [math] \frac{\partial \mathcal {L} }{\partial x_1} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x_1} \right ) [/math]
- [math] g(m_1-m_2)= \frac{d}{dt} \left (( m_1 + m_2) \dot x_1\right ) [/math]
- [math] = ( m_1 + m_2) \ddot x_1 [/math]
- [math] \ddot x_1= \frac{(m_1-m_2)}{ ( m_1 + m_2)} g [/math]
Block Sliding on a Wedge
A block slides down an incline of elevation [math]\alpha[/math] that is free to move on the table.
How long does it take the block to reach the bottom if it is released a distance [math]l[/math] from the top.
Let
- [math]q_1 =[/math] distance of block from the top of the incline
- [math]q_2 =[/math] distance incline moves from its starting point.
- [math]U=-m_1g q_1 \sin \alpha[/math]
- [math]T_m =[/math] Kinetic energy of the block of mass m
- [math]T_M =[/math] kinetic energy of the incline of mass M
- [math]T_M = \frac{1}{2} Mq_2^2[/math]
The kinetic energy of the block is a combination of the velocity of the block down the incline and the velocity of the incline. As the block moves down the inline, the incline moves.
- [math]\vec {v}_m = (\dot q_1 cos \alpha + \dot q_2) \hat i + \dot q_1 \sin \alpha \hat j[/math]
- [math]T_m = \frac{1}{2} m ( \dot q_1^2 + q_2^2 + 2 \dot q_1 \dot q_2 \cos \alpha)[/math]
- [math]\mathcal L(q_1, q_2, \dot q_1, \dot q_2;t) = T - U = \left ( \frac{1}{2} m ( \dot q_1^2 + q_2^2 + 2 \dot q_1 \dot q_2 \cos \alpha)\right ) + \frac{1}{2} Mq_2^2+ mg q_1 \sin \alpha[/math]
- [math] = \frac{1}{2} m ( \dot q_1^2+ 2 \dot q_1 \dot q_2 \cos \alpha) + \frac{1}{2} (M+m) \dot q_2^2+ mg q_1 \sin \alpha[/math]
for q_1
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q_1} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q_1} \right ) [/math]
- [math] mg \sin \alpha = \frac{d}{dt} \left ( m( \dot q_1 + \dot q_2 \cos \alpha)\right ) [/math]
- [math] = m( \ddot q_1 + \ddot q_2 \cos \alpha)[/math]
for q_2
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q_2} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q_2} \right ) [/math]
- [math] 0 = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q_2} \right ) [/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \dot q_2} \right ) = M \dot q_2 + m ( \dot q_2 + \dot q_2 \cos \alpha) = constant [/math]
- [math]\Rightarrow \ddot q_2 = - \frac{m}{M+m}\ddot q_1 \cos \alpha[/math]
substituting q_2 into q_1
- [math] g \sin \alpha = \ddot q_1 + \ddot q_2 \cos \alpha[/math]
- [math] = \ddot q_1 + \left (- \frac{m}{M+m}\ddot q_1 \cos \alpha \right ) \cos \alpha[/math]
- [math] = \ddot q_1 \left (1 - \frac{m}{M+m} \cos^2 \alpha \right )[/math]
- [math] \ddot q_1 = \frac{ g \sin \alpha}{\left (1 - \frac{m}{M+m} \cos^2 \alpha \right )}[/math]
- Note
- If [math]\alpha[/math] is 90 degrees then [math]\ddot q_1 = g[/math]
The acceleration is constant so one may use constant acceleration equations to find the fall time
- [math]l = \frac{1}{2} \ddot q_1 t^2[/math]
- [math]\Rightarrow t = \sqrt{\frac{2l}{\ddot q_1}} = \sqrt{\frac{2l}{ \frac{ g \sin \alpha}{\left (1 - \frac{m}{M+m} \cos^2 \alpha \right )}}}[/math]
- [math]= \sqrt{\frac{2l \left (1 - \frac{m}{M+m} \cos^2 \alpha \right )}{g \sin \alpha}}[/math]
- Note
- If M is infinite then [math]t = \sqrt{\frac{2l}{g \sin \alpha}}[/math]
Lagrange Multipliers
The method of Lagrange multipliers is a means to incorporate the constraints of a system into the Euler-Lagrange equation.
consider the problem of a disk rolling down an incline plane without slipping.
If we assume the incline does not move then we have 2 degrees of freedom for the disk.
Let [math]s[/math] represent the distance from the top of the incline and [math]\theta[/math] an angle of disk rotation.
The "no-slip" constraint means that there is a force of friction; which does no work by the way.
To roll without slipping requires that
- [math]\dot s = R \dot \theta[/math]
let
- [math]f(s,\theta) \equiv s-R \theta[/math]
then
- [math]\frac{d f}{d t} = \sum \frac{\partial f}{\partial q_i} \frac{d q_i}{dt} + \frac{\partial f}{\partial t} = \dot s - R \dot \theta = 0[/math]
The above constraint is holonomic since the constraint on the velocities can be integrated to give a relationship between the coordinates. Non-holonomic constraints do not have this property.
Constraints in Differential form
Using the above example we can generalize the constraint equation to take the form of a differential equation.
let
- [math]\sum A_i \dot q_i + B =0[/math]
where
- [math]A \equiv \frac{\partial f}{\partial q_i} \;\;\;\;\; B \equiv \frac{\partial f}{\partial t} \;\;\;\;\; f= f(q_i,t)[/math]
then
- [math]\frac{d f}{dt} = \sum \frac{\partial f}{\partial q_i} + \frac{\partial f}{\partial t} =0[/math]
since the total derivative with respect to time is zero , the function is a constant in time
- [math]f(q_i,t) = \mbox{constant} \Rightarrow[/math] A holonomic constraint (doesn't depend on other variables)
The advantage of having the constraint in differential form is that instead of incorporating their integrated form into the problem we add them to the Euler-Lagrange equation.
Incorporate the constraints into Euler-Lagrange Equations
Consider a system having [math]m[/math] constraints with [math]s[/math] generalized coordinate parameters.
For the case of time independent constraints, the [math]\ell[/math]-th constraint equation equation for the constraint function [math]f_{\ell}[/math] may be represented as
- [math] \sum_{\ell} \frac{\partial f_{\ell} }{\partial q_i}= 0[/math]
let [math]\lambda_{\ell}[/math] be an undetermined coefficient such that
- [math]\lambda_{\ell} \sum_{\ell} \frac{\partial f_{\ell} }{\partial q_i}= 0[/math]
The Euler-Lagrange equation is
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) \right ] =0 [/math]
we can add Lagrange multiplier to the above equation without changing it
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) \right ] =0 = \sum_{\ell} \lambda_{\ell} \frac{\partial f_{\ell} }{\partial q_i}[/math]
but this is more than just equating terms that are equal to zero.
consider a system in cartesian coordinates such that
- [math]T = \frac{1}{2} m(\dot x^2 + \dot y^2 + \dot z^2)[/math]
the above coordinates may be written in term of generalized coordinates or in other words they can be expressed as functions of q_i such that
- [math]x=x(q_1,q_2, \cdots q_s) = x(q)[/math] the same is try for y and z
the total derivative with respect to time is given by the chain rule as
- [math]\dot x = \frac{\partial x}{\partial q_1}\frac{\partial q_1}{\partial t} +\frac{\partial x}{\partial q_2}\frac{\partial q_2}{\partial t} \cdots +\frac{\partial x}{\partial q_s}\frac{\partial q_s}{\partial t}[/math]
- [math]= \sum_{k=1}^s \frac{\partial x}{\partial q_k} \dot q_k = \dot{x}(q,\dot q)[/math]
- [math]T = \frac{1}{2} m(\dot x^2(q,\dot q) + \dot y^2(q,\dot q) + \dot z^2(q,\dot q))[/math]
- [math]\frac{\partial T}{\partial \dot q_j} = m \left (\dot x \frac{\partial \dot x}{\partial \dot q_j} + \dot y \frac{\partial \dot y}{\partial \dot q_j} + \dot z \frac{\partial \dot z}{\partial \dot q_j} \right )[/math]
since
- [math]\dot x = \sum_{k=1}^s \frac{\partial x}{\partial q_k} \dot q_k [/math]
then
- [math]\frac{ \partial \dot x}{\partial \dot q_j} = \frac{\partial }{\partial q_j} \sum_{k=1}^s \frac{\partial x}{\partial q_k} \dot q_k = \frac{\partial x}{\partial q_j}[/math] only the jth term survives the derivative of the sum
- [math]\frac{\partial T}{\partial \dot q_j} = m \left (\dot x \frac{\partial \dot x}{\partial \dot q_j} + \dot y \frac{\partial \dot y}{\partial \dot q_j} + \dot z \frac{\partial \dot z}{\partial \dot q_j} \right )[/math]
- [math] = m \left (\dot x \frac{\partial x}{\partial q_j} + \dot y \frac{\partial y}{\partial q_j} + \dot z \frac{\partial z}{\partial q_j} \right )[/math]
take derivative of both sides with respect to time
- [math]\frac{d}{dt} \left ( \frac{\partial T}{\partial \dot q_j} \right ) = m \left (\ddot x \frac{\partial x}{\partial q_j} + \ddot y \frac{\partial y}{\partial q_j} + \ddot z \frac{\partial z}{\partial q_j} \right )+ m \left (\dot x \frac{d}{dt} \left ( \frac{\partial x}{\partial q_j}\right ) + \dot y\frac{d}{dt} \left ( \frac{\partial y}{\partial q_j}\right ) + \dot z \frac{d}{dt} \left ( \frac{\partial z}{\partial q_j} \right )\right )[/math]
since
- [math]\frac{d}{dt} \left ( \frac{\partial x}{\partial q_j}\right ) = \frac{d}{d q_j} \left ( \frac{\partial x}{\partial t}\right ) = \frac{\partial \dot x}{\partial q_j}[/math] here the total and partial derivatives are interchangeable
- [math]m \left (\dot x \frac{d}{dt} \left ( \frac{\partial x}{\partial q_j}\right ) \right ) = m \dot x \frac{\partial \dot x}{\partial q_j} = \frac{\partial }{\partial q_j} (\frac{1}{2} m \dot x^2)[/math]
and
- [math]F_x \equiv m \ddot x[/math]
Then
- [math]\frac{d}{dt} \left ( \frac{\partial T}{\partial \dot q_j} \right ) = m \left (\ddot x \frac{\partial x}{\partial q_j} + \ddot y \frac{\partial y}{\partial q_j} + \ddot z \frac{\partial z}{\partial q_j} \right )+ m \left (\dot x \frac{d}{dt} \left ( \frac{\partial x}{\partial q_j}\right ) + \dot y\frac{d}{dt} \left ( \frac{\partial y}{\partial q_j}\right ) + \dot z \frac{d}{dt} \left ( \frac{\partial z}{\partial q_j} \right )\right )[/math]
- [math]= F_x \frac{\partial x}{\partial q_j}+ F_y \frac{\partial y}{\partial q_j}+ F_z \frac{\partial z}{\partial q_j} + \frac{\partial }{\partial q_j} (\frac{1}{2} m (\dot x^2+\dot y^2+\dot z^2)[/math]
- [math]= Q_j + \frac{\partial T}{\partial q_j} \equiv [/math] Lagrange's equations of motion
where
[math]Q_j = F_x \frac{\partial x}{\partial q_j}+ F_y \frac{\partial y}{\partial q_j}+ F_z \frac{\partial z}{\partial q_j} = \sum_{\ell} \lambda_{\ell} \frac{\partial f_{\ell}}{\partial q_j}[/math]
[math]Q_j =\sum_{\ell} \lambda_{\ell} \frac{\partial f_{\ell}}{\partial q_j}[/math] Generalized forces of constraint [math]Q_j[/math]
disk rolling down incline place using multipliers
Returning to the problem of a disk rolling without slipping down an incline place
- [math]T = \frac{1}{2} \dot s^2 + \frac{1}{2} I \dot \phi^2 \;\;\;\;\;\;\; I = \frac{1}{2}MR^2[/math]
- [math]U = Mg(l-s) \sin \theta[/math]
- [math]L = T - U = \frac{1}{2} \dot s^2 + \frac{1}{4} MR^2 \dot \phi^2 - Mg(l-s) \sin \theta[/math]
- [math]f(s,\theta) = s - R \phi[/math]
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) \right ] = \sum_{\ell} \lambda_{\ell} \frac{\partial f_{\ell} }{\partial q_i}[/math]
- [math]\Rightarrow[/math]
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial \theta} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right ) \right ] - \lambda \frac{\partial f }{\partial \theta}=0[/math]
- [math]\frac{1}{2} MR^2 \ddot \theta^2 - \lambda R = 0[/math]
- [math]\Rightarrow \lambda = \frac{1}{2} MR^2 \ddot \theta^2 = \frac{1}{2} M \ddot s^2[/math]
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial s} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot s} \right ) \right ] - \lambda \frac{\partial f }{\partial s}=0[/math]
- [math] Mg \sin \theta - M\ddot s - \lambda = Mg \sin \theta -M\ddot s -\frac{1}{2} MR^2 \ddot s^2 = 0[/math]
- [math]\Rightarrow \ddot s^2 = \frac{2}{3}g \sin \theta[/math]
substituting
- [math]\Rightarrow \lambda =\frac{1}{2} MR^2 \ddot s^2=\frac{1}{2} MR^2\frac{2}{3}g \sin \theta = \frac{1}{3}Mg \sin \theta[/math]
and
- [math]\frac{1}{2} MR^2 \ddot \theta^2 - \lambda R = 0 \Rightarrow \ddot \theta^2 = \frac{2}{3R}g \sin \theta [/math]
- [math]Q_s = \lambda \frac{\partial f}{\partial y} = \lambda = \frac{1}{3}Mg \sin \theta = F_f[/math]
- [math]Q_{\theta} = \lambda \frac{\partial f}{\partial \theta} = -\lambda R = \frac{1}{3}MgR \sin \theta = -\tau[/math]
Falling ladder
consider a ladder of length L leaning against a frictionless wall and sitting on a frictionless floor.
Since everything is frictionless the ladder will begin to fall.
Find the equation of motion for the ladder.
There are 3 degrees of freedom; The the [math]x[/math] and [math]y[/math] position of the ladder and the angle, [math]\theta[/math], the ladder makes with respect to the floor.
There are 2 constraint equations
- [math]f_1 = x - \frac{L}{2} \sin \theta[/math]
- [math]f_2 = y - \frac{L}{2} \sin \theta[/math]
- [math]T = \frac{1}{2} m(\dot x^2 + \dot y^2) + \frac{1}{2} I \dot \theta^2
[/math]
- [math]U = mgy[/math]
- [math]\mathcal L = \frac{1}{2} m(\dot x^2 + \dot y^2) + \frac{1}{2} I \dot \theta^2 -mgy[/math]
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) \right ] =\lambda_{\ell} \sum_{\ell} \frac{\partial f_{\ell} }{\partial q_i}[/math]
for [math]x[/math]:
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial x} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot x} \right ) \right ] =\lambda_1 \frac{\partial f_1 }{\partial x}+\lambda_2 \frac{\partial f_2 }{\partial x} [/math]
- [math] \Rightarrow m \ddot x = \lambda_1[/math]
But from the constraint equation f_1
- [math] x = \frac{L}{2} \sin \theta \Rightarrow \dot x = \frac{L}{2} \cos \theta \dot \theta \Rightarrow \ddot x = \frac{L}{2} \left ( \ddot \theta \cos \theta - \dot \theta^2 \sin \theta \right )[/math]
thus
- [math] \lambda_1 = m \frac{L}{2} \left ( \ddot \theta \cos \theta - \dot \theta^2 \sin \theta \right )[/math]
For [math]y[/math]:
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial y} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot y} \right ) \right ] =\lambda_1 \frac{\partial f_1 }{\partial y}+\lambda_2 \frac{\partial f_2 }{\partial y} [/math]
- [math] \Rightarrow m \ddot y + mg = \lambda_2[/math]
But from the constraint equation f_2
- [math] y = \frac{L}{2} \cos \theta \Rightarrow \dot y = -\frac{L}{2} \sin \theta \dot \theta \Rightarrow \ddot y = \frac{L}{2} \left ( -\ddot \theta \sin \theta - \dot \theta^2 \cos \theta \right )[/math]
thus
- [math] \lambda_2 = m \frac{L}{2} \left ( -\ddot \theta \sin \theta - \dot \theta^2 \cos \theta \right ) + mg[/math]
for [math]\theta[/math]:
- [math] \left [ \left ( \frac{\partial \mathcal {L} }{\partial \theta} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right ) \right ] =\lambda_1 \frac{\partial f_1 }{\partial \theta}+\lambda_2 \frac{\partial f_2 }{\partial \theta} [/math]
- [math] \Rightarrow \frac{mL^2}{12} \ddot \theta = -\lambda_1 ( \frac{L}{2}\cos \theta) + \lambda_2 ( \frac{L}{2}\sin \theta) [/math]
substituting in for [math] \lambda_1[/math] and [math]\lambda_2[/math]
- [math] \Rightarrow \frac{mL^2}{12} \ddot \theta = -\left [ m \frac{L}{2} \left ( \ddot \theta \cos \theta - \dot \theta^2 \sin \theta \right ) \right ] ( \frac{L}{2}\cos \theta) + \left [ m \frac{L}{2} \left ( -\ddot \theta \sin \theta - \dot \theta^2 \cos \theta \right ) + mg \right ] ( \frac{L}{2}\sin \theta) [/math]
- [math] \frac{L}{3} \ddot \theta = -\left [ \left ( \ddot \theta \cos \theta - \dot \theta^2 \sin \theta \right ) \right ] ( L\cos \theta) + \left [ \left ( -\ddot \theta \sin \theta - \dot \theta^2 \cos \theta \right ) + \frac{2g}{L} \right ] ( L\sin \theta) [/math]
- [math] \frac{1}{3} \ddot \theta = -\left [ \left ( \ddot \theta \cos \theta - \dot \theta^2 \sin \theta \right ) \right ] ( \cos \theta) + \left [ \left ( -\ddot \theta \sin \theta - \dot \theta^2 \cos \theta \right ) + \frac{2g}{L} \right ] ( \sin \theta) [/math]
- [math]= -\ddot \theta \cos^2 \theta + \dot \theta^2 \sin \theta \cos \theta -\ddot \theta \sin^2 \theta -\dot \theta^2 \cos \theta \sin \theta + \frac{2g}{L} \sin \theta[/math]
- [math]= -\ddot \theta (\cos^2 \theta +\sin^2 \theta)+ \frac{2g}{L} \sin \theta[/math]
- [math]\Rightarrow \ddot \theta = \frac{3g}{2L} \sin \theta[/math]
- [math]Q_{\theta} = \lambda_1 \frac{\partial f_1}{\partial \theta} +\lambda_2 \frac{\partial f_2}{\partial \theta}[/math]
- [math]= mg \frac{L}{2} \sin \theta - \frac{mL^2}{4} \ddot \theta = \vec r \times \vec{F}_g - I \alpha[/math]
- [math] I \alpha[/math] = torque resulting from normal force of wall on ladder ( choose point of ladder's contact with floor as the point of rotation)
More Examples
2-D Central Force
Consider a particle of mass [math]m[/math] that is constrained to move in 2-D due to a potential U(2).
Since this is a 2-D problem, lets use polar coordinates.
- [math]T = \frac{1}{2} m \left ( \dot r^2 + r^2 \dot \phi^2\right )[/math]
- [math]\mathcal L = \frac{1}{2} m \left ( \dot r^2 + r^2 \dot \phi^2\right ) - U(r)[/math]
For the [math]\phi[/math] generalized coordinate parameter
- [math] \frac{\partial \mathcal {L} }{\partial \phi} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi} \right ) [/math]
- [math] 0 = \frac{d}{dt} \left ( m r^2 \dot \phi \right ) \Rightarrow m r^2 \dot \phi = [/math]constant
for the [math]r[/math] generalized coordinate parameter
- [math] \frac{\partial \mathcal {L} }{\partial r} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot r} \right ) [/math]
- [math] m r \dot \phi^2 - \frac{\partial U(r)}{\partial r} = m \ddot r [/math]
let
- [math]p_{\phi} \equiv m r^2 \dot \phi = [/math]constant
then
- [math] m \ddot r= m r \dot \phi^2 - \frac{\partial U(r)}{\partial r} [/math]
- [math] = \frac{p_{\phi}^2}{m} \frac{1}{r^3}- \frac{\partial U(r)}{\partial r}[/math]
Particle confined on a cylinder
Consider a particle of mass [math]m[/math] that is experiencing a force [math]\vec F=-k \vec r[/math] and is constrained to move on a frictionless cylinder of radius [math]R[/math].
Find the equation(s) to describe its motion.
Since the particle is constrained by a cylinder it seems worthwhile to use cylindrical coordinates to describe its motion.
- [math]\vec{r} = r \hat{r} + z \hat{k}[/math]
- [math]\vec{v}=\vec{\dot{r}} = \dot{r} \hat{r} + r \dot{\phi} \hat{\phi} + \dot{z} \hat{k}[/math]
- [math]\vec{a} = \left ( \ddot{r} -r\dot{\phi}^2 \right) \hat{r} + \left ( 2\dot{r} \dot{\phi} +r \ddot{\phi} \right ) \hat{\phi} + \ddot{z} \hat{k}[/math]
- [math]T = \frac{1}{2} m v^2 = \frac{1}{2} m \left ( R^2 \dot \phi^2 + \dot z^2\right )[/math]
- [math]\vec F = - k \vec r = -k (R \hat{r} + z \hat{k})[/math]
to determine if the force is conservative.
Test if
- [math]\vec \nabla \times \vec F =0[/math]
- [math]\vec \nabla \times \vec F = \left ( \begin{matrix} \hat r & \hat \phi & \hat k \\ \frac{\partial}{\partial r} & \frac{1}{r} \frac{\partial}{\partial \phi} & \frac{\partial}{\partial z} \\-kr & 0 &-kz \end{matrix} \right ) = 0 [/math]
The potential energy for this force may be defined according to the work integral
- [math]U(r) = - W = - \int \vec F \cdot d \vec r = - \int -k ( r \hat{r} + z \hat{k}) \cdot (dr \hat r + r d \phi \hat \phi + dz \hat k) [/math]
- [math]=\frac{1}{2} k ( R^2 +z^2)[/math]
- [math]\mathcal L = \frac{1}{2} m \left ( R^2 \dot \phi^2 + \dot z^2\right ) - \frac{1}{2} k ( R^2 +z^2)[/math]
- [math] \frac{\partial \mathcal {L} }{\partial z} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot z} \right ) [/math]
- [math]-kz = m\ddot z[/math]
- [math] \Rightarrow z = A \cos(\omega t - \delta)[/math] simple harmonic motion in the z coordinate
- [math] \frac{\partial \mathcal {L} }{\partial \phi} = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi} \right ) [/math]
- [math]0 = \frac{d}{dt} \left ( mR^2 \dot \phi \right ) [/math]
- [math]\Rightarrow[/math] angular momentum is conserved
ball in a bowl
consider a ball of mass [math]m[/math] and radius [math] r[/math] is constrained to roll without slipping spherical bowl of radius [math]R[/math] that is in a gravitational field.
The generalized coordinate functions for this problem are [math] \phi[/math] and [math]\theta[/math] where [math]\phi[/math] is the rotation angle of the ball and [math]\theta[/math] is the angle of inclination of the ball with respect to the cylinders central axis.
- [math] T = \frac{1}{2} \left ( (R-r)^2 \dot \theta^2 + I \dot \phi^2 \right )[/math]
- [math]I_{ball} = \frac{2}{5} mr^2[/math]
- [math]U = mg \left ( R - (R-r) \cos \theta \right )[/math]
- [math]\mathcal L = \frac{1}{2} \left ( m(R-r)^2 \dot \theta^2 + I \dot \phi^2 \right ) - mg \left ( R - (R-r) \cos \theta \right )[/math]
constraint equation
- [math]f_1(\theta, \phi) = R \theta -r \phi = 0[/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) = \sum_{\ell} \lambda_{\ell} \frac{\partial f_{\ell} }{\partial q_i}[/math]
for the [math]\phi[/math] generalized coordinate function:
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \phi} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi} \right )= \lambda_1 \frac{\partial f_1 }{\partial \phi}[/math]
- [math] 0 - I\ddot \phi = \lambda_1(-r) \Rightarrow \lambda_1 = \frac{I \ddot \phi}{r}[/math]
for the [math]\theta[/math] generalized coordinate function:
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \theta} \right ) - \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right )= \lambda_1 \frac{\partial f_1 }{\partial \theta}[/math]
- [math] -mg(R-r) \sin \theta - m(R-r)^2\ddot \theta = \lambda_1R [/math]
- [math] -mg \sin \theta - m(R-r)\ddot \theta = \lambda_1 \frac{r}{R-r} = \frac{I \ddot \phi}{r}\frac{r}{R-r}[/math]
The constraint equation
- [math]f_1(\theta, \phi) = R\theta -r \phi = 0 \Rightarrow R\ddot \theta = r \ddot \phi[/math]
- [math] -mg \sin \theta - m(R-r) \ddot \theta = \frac{I \ddot \phi}{R-r} = \frac{\frac{2}{5}mr^2}{R-r} \frac{R\ddot \theta}{r}[/math]
- [math] g \sin \theta + (R-r)\ddot \theta = -\frac{2}{5} \frac{r R \ddot \theta}{R-r}[/math]
- [math] \left ( R-r+ \frac{2rR}{5(R-r)} \right ) \ddot \phi = -g \sin \theta [/math]
- [math] \ddot \phi = -\left(\frac{g}{ R-r+ \frac{2rR}{5(R-r)}}\right )\sin \theta \approx - \omega^2 \theta [/math]
- [math]\omega = [/math]oscillation frequency
Double Pendulum
The double pendulum problem in 2-D has two objects (4 degrees of freedom) and two constraints.
The number of generalized coordinates = 4-2 = 2
Choosing the two angles [math]\phi_1[/math] and [math]\phi_2[/math]
In cartesian coordinates one may write the position and velocity of the two objects as
- Object 1
- [math]x_1 = l_1 \sin \phi_1 \;\;\;\;\; y_1 = -l_1 \cos\phi_1[/math]
- [math] \dot x_1 = l_1 \cos \phi_1 \dot \phi_1 \;\;\;\;\; \dot y_1 = l_1 \sin \phi_1 \dot \phi_1[/math]
- Object 2 is a little more complicated as its position depends on object 1
- [math]x_2 = l_1 \sin \phi_1 + l_2 \sin \phi_2 \;\;\;\;\; y_1 = -l_1 \cos \phi_1-l_2 \cos \phi_2[/math]
- [math] \dot x_1 = l_1 \sin \phi_1 \dot \phi + l_2 \sin \phi_2 \dot \phi_2\;\;\;\;\; \dot y_1 = l_1 \sin \phi_1 \dot \phi_1 + l_2 \sin \phi_2 \dot \phi_2[/math]
- [math]T = \frac{1}{2}( m_1 \dot x_1^2 + m_2 \dot x_2^2)[/math]
- [math]= \frac{1}{2} (m_1 l_1^2 \dot \phi_1^2 + m_2 ( l_1^2 \dot \phi_1^2 + 2 l_1 l_2 \cos(\phi_1-\phi_2) \dot \phi_1 \dot \phi_2 + l_2^2 \dot \phi_2^2))[/math]
- [math]= \frac{1}{2} (m_1+m_1) l_1^2 \dot \phi_1^2 + m_2 l_1 l_2 \cos(\phi_1-\phi_2) \dot \phi_1 \dot \phi_2 + \frac{1}{2} m_2 l_2^2 \dot \phi_2^2[/math]
- [math]U = m_1y_1 + m_2y_2[/math]
- [math]= -m_1gl_1 \cos(\phi_1) - m_2g(l_1\cos \phi_1 + l_2 \cos \phi_2)[/math]
- [math]= -(m_1+m_2)gl_1 \cos \phi_1 - m_2g l_2 \cos \phi_2[/math]
- [math]\mathcal L =\frac{1}{2} (m_1+m_1) l_1^2 \dot \phi_1^2 + m_2 l_1 l_2 \cos(\phi_1-\phi_2) \dot \phi_1 \dot \phi_2 + \frac{1}{2} m_2 l_2^2 \dot \phi_2^2 + (m_1+m_2)gl_1 \cos \phi_1 + m_2gl_2 \cos \phi_2[/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial q} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot q} \right ) [/math]
for the [math]\phi_1[/math] generalize coordinate paramter
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \phi_1} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi_1} \right ) [/math]
- [math]-m_2 l_1 l_2 \sin(\phi_1-\phi_2) \dot \phi_1 \dot \phi_2 - (m_1+m_2)gl_1 \sin \phi_1 = \frac{d}{dt} \left ( (m_1+m_1) l_1^2 \dot \phi_1 + m_2 l_1 l_2 \cos(\phi_1-\phi_2) \dot \phi_2 \right ) [/math]
- [math]= (m_1+m_1) l_1^2 \ddot \phi_1 - m_2 l_1 l_2 \sin(\phi_1-\phi_2) (\dot \phi_1-\dot \phi_2) \dot \phi_2+ m_2 l_1 l_2 \cos(\phi_1-\phi_2) \ddot \phi_2 [/math]
- if I assume small oscillations
- [math]- (m_1+m_2)gl_1 \phi_1= (m_1+m_1) l_1^2 \ddot \phi_1 + m_2 l_1 l_2 \cos(\phi_1-\phi_2) \ddot \phi_2 [/math]
- [math]- gl_1 \phi_1= l_1^2 \ddot \phi_1 + \frac{m_2}{(m_1+m_2)} l_1 l_2 \ddot \phi_2 [/math]
- [math]\ddot \phi_1 + \alpha \beta \ddot \phi_2 + \omega_0^2 \phi_1= 0[/math]
where
- [math]\alpha = \frac{m_2}{(m_1+m_2)} \;\;\;\; \beta = \frac{l_2}{l_1} \;\;\;\;\; \omega_0^2 = \frac{g}{l_1}[/math]
for the [math]\phi_2[/math] generalize coordinate paramter
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \phi_2} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \phi_2} \right ) [/math]
- [math]m_2 l_1 l_2 \sin(\phi_1-\phi_2) \dot \phi_1 \dot \phi_2 - m_2gl_2 \sin \phi_2 = \frac{d}{dt} \left ( m_2 l_1 l_2 \cos(\phi_1-\phi_2) \dot \phi_1 + m_2 l_2^2 \dot \phi_2 \right ) [/math]
- [math]= m_2 l_1 l_2 \cos(\phi_1-\phi_2) \ddot \phi_1 - m_2 l_1 l_2 \sin(\phi_1-\phi_2)(\dot \phi_1- \dot \phi_2) \dot \phi_1 + m_2 l_2^2 \ddot \phi_2 [/math]
- assuming small oscillations
- [math] - m_2gl_2 \sin \phi_2 = m_2 l_1 l_2 \ddot \phi_1 + m_2 l_2^2 \ddot \phi_2 [/math]
- [math]\ddot \phi_1 + \beta \ddot \phi_2 + \omega_0^2 \phi_2 = 0[/math]
Solving coupled ODEs
The double pendulum's motion for small angles is described by a set of coupled , non-linear, second order ordinary differential equations.
- [math]\ddot \phi_1 + \alpha \beta \ddot \phi_2 + \omega_0^2 \phi_1= 0[/math]
- [math]\ddot \phi_1 + \beta \ddot \phi_2 + \omega_0^2 \phi_2 = 0[/math]
where
- [math]\alpha = \frac{m_2}{(m_1+m_2)} \;\;\;\; \beta = \frac{l_2}{l_1} \;\;\;\;\; \omega_0^2 = \frac{g}{l_1}[/math]
create a linear combination of the ODEs by adding them together using an arbitrary constant
- [math]\ddot \phi_1 + \alpha \beta \ddot \phi_2 + \omega_0^2 \phi_1= 0[/math]
- [math]+ \gamma \left ( \ddot \phi_1 + \beta \ddot \phi_2 + \omega_0^2 \phi_2 = 0 \right ) [/math]
- [math]\Rightarrow (1+\gamma)\ddot \phi_1 + ( \alpha + \gamma ) \beta \ddot \phi_2 + \omega_0^2 \left ( \phi_1 + \gamma \phi_2 \right )=0 [/math]
Now require that the raio of the coefficients for the non-differential terms [math]\frac{r}{1}[/math]
be equal to the ratio of the coefficients for the double differential terms
- [math]\frac{ ( \alpha + \gamma ) \beta}{(1+\gamma)} = \frac{\gamma}{1} [/math]
- [math] ( \alpha + \gamma ) \beta = \gamma(1+\gamma) [/math]
- [math] \alpha \beta+ \gamma \beta = \gamma +\gamma^2[/math]
- [math]\gamma^2 + ( 1- \beta)\gamma -\alpha \beta =0 [/math]
- [math] \Rightarrow \gamma = \frac{-( 1- \beta) \pm \sqrt{( 1- \beta)^2-4(-\alpha \beta)}}{2}[/math]
The differential equation for this linear combination may be written as
- [math](1+\gamma)\ddot \phi_1 + ( \alpha + \gamma ) \beta \ddot \phi_2 + \omega_0^2 \left ( \phi_1 + \gamma \phi_2 \right )[/math]
- [math] \ddot \phi_1 + \frac{( \alpha + \gamma )}{(1+\gamma)} \beta \ddot \phi_2 + \frac{\omega_0^2 }{(1+\gamma)}\left ( \phi_1 + \gamma \phi_2 \right )[/math]
- [math]\frac{d^2}{dt^2}\left ( \phi_1 + \gamma \phi_2 \right )= - \frac{\omega_0^2}{1+\gamma} ( \phi_1 + \gamma \phi_2)[/math]
A normal coordinate is defined such that
- [math]\xi \equiv \phi_1 + \gamma \phi_2 [/math]
Then the ODE looks like an oscillator
- [math]\ddot \xi = - \frac{\omega_0^2}{1+\gamma} \xi[/math]
- [math]\Rightarrow \omega = \frac{\omega_0}{\sqrt{1+\gamma}}[/math]
We have two possible solutions
"in phase"
- [math]\xi_+ \equiv \phi_1 + \gamma_+ \phi_2 \;\;\;\;\; \omega = \frac{\omega_0}{\sqrt{1+\gamma_+}} [/math]
- [math] \Rightarrow \gamma_+ = \frac{-( 1- \frac{l_2}{l_1}) + \sqrt{( 1- \frac{l_2}{l_1})^2-4(-\frac{m_2}{(m_1+m_2)} \frac{l_2}{l_1})}}{2}[/math]
"out of phase"
- [math]\xi_- \equiv \phi_1 + \gamma_- \phi_2 \;\;\;\;\; \omega = \frac{\omega_0}{\sqrt{1+\gamma_-}} [/math]
- [math] \Rightarrow \gamma_- = \frac{-( 1- \frac{l_2}{l_1}) - \sqrt{( 1- \frac{l_2}{l_1})^2-4(-\frac{m_2}{(m_1+m_2)} \frac{l_2}{l_1})}}{2}[/math]
- if [math]l_1=l_2=l[/math] & [math] m_1=m_2=m[/math]
Then
- [math]\alpha= \frac{1}{2} \;\;\;\; \beta = 1 \;\;\;\; \gamma = \pm \frac{1}{\sqrt 2}[/math]
the "in phase" oscillation
- [math]\xi = \phi_1 + \frac{1}{\sqrt 2} \phi_2 \;\;\;\; \omega = \sqrt{\frac{2}{\sqrt{2}+1}} \frac{g}{l}[/math]
the "out of phase" oscillation
- [math]\xi = \phi_1 - \frac{1}{\sqrt 2} \phi_2 \;\;\;\; \omega = \sqrt{\frac{2}{\sqrt{2}-1}} \frac{g}{l}[/math]
- Note
- The frequency for the case when the two pendulums are oscillating in phase is lower than when they are out of phase.
Bead on a spinning hoop
A bead of mass [math]m[/math] is threaded on a frictionless circular wire hoop or radius [math]R[/math] that is rotating at a constant velocity [math]\dot \phi[/math]
The bead makes and angle [math]\theta[/math] with respect to the vertical.
Find equilibrium positions for the bead where it remains at a constant [math]\theta[/math] in terms of the centripetal acceleration ( [math] \omega^2r[/math] )
The bead has two velocity components.
If the bead is moving up or down the circular hoop then
- [math]v_t = R \dot \theta[/math]
The bead is moving with the circular hoop as the hoop is rotated at a constant angular velocity [math]\omega[/math]
- [math]v_{\phi} = R \sin \theta \omega[/math]
- [math]T = \frac{1}{2} m \left ( R^2 \dot \theta^2 + R^2 \sin^2 \theta \omega^2 \right )[/math]
- [math]U = mgy = mgR(1-\cos \theta)[/math]
The Lagrangian for the bead is
- [math]\mathcal L = \frac{1}{2} m \left ( R^2 \dot \theta^2 + R^2 \sin^2 \theta \omega^2 \right ) - mgR(1-\cos \theta)[/math]
- [math] \frac{\partial \mathcal {L} }{\partial \theta } = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right ) [/math]
- [math]m R^2 \omega^2 \sin \theta \cos \theta - mgR \sin \theta = mR^2 \ddot \theta[/math]
- [math]\Rightarrow \ddot \theta = \left ( \omega^2 \cos \theta - \frac{g}{R} \right ) \sin \theta[/math]
For the bead to be in equilibrium the acceleration should be zero
- [math]\ddot \theta = 0 \Rightarrow \left ( \omega^2 \cos \theta - \frac{g}{R} \right ) \sin \theta = 0[/math]
if [math]\theta = 0 or \pi [/math] degrees then the bead is at the top or bottom of the hoop
another way is if
- [math]\left ( \omega^2 \cos \theta - \frac{g}{R} \right )=0[/math]
or
- [math]\cos \theta = \frac{g}{\omega^2 R}[/math]
if
- [math]\cos \theta = \frac{g}{\omega^2 R}\gt 1 \Rightarrow \frac{g}{ R}\gt \omega^2 [/math]
Then only [math]\theta = 0[/math] and [math]\pi[/math] are equilibrium positions, [math]\omega[/math] is too small , the circular ring is rotating too slowly.
if
- [math] \omega^2 \ge \frac{g}{ R}[/math]
then
- [math]\theta = \cos^{-1} \left ( \frac{g}{\omega^2 R} \right )[/math]
stability
There are two cases depending on [math]\omega[/math]
- When [math]\omega^2 \lt \frac{g}{ R}[/math] and [math] \theta \approx 0[/math]
then
- [math]\Rightarrow \ddot \theta = \left ( \omega^2 \cos \theta - \frac{g}{R} \right ) \sin \theta= \left ( \omega^2 (1)- \frac{g}{R} \right ) \theta = - \omega^{\prime\;\;2}\theta[/math]
- [math]\Rightarrow[/math] oscillating motion due to gravity pulling it down any movement away from the bottom of the hoop will result in a net force back towards the bottom of the hoop to
- [math] \omega^{\prime} = \sqrt{\frac{g}{R} - \omega^2}[/math] oscillation frequency if bead is displaced a small amount from the bottom of the hoop
If[math] \theta \approx \pi[/math]
Then
- [math] \ddot \theta = \left ( -\omega^2 - \frac{g}{R} \right ) \theta = - \omega^{\prime\;\;2}\theta[/math]
If the bead moves away from [math]\theta=\pi[/math] then you will have oscillation again but you won't return to [math]\theta= \pi[/math] as gravity is pulling the bead down and the normal force only cancels this at [math]\theta = \pi[/math]. This is an unstable critical point.
[math] \omega^{\prime} = \sqrt{\frac{g}{R} + \omega^2}[/math]
- When [math]\omega^2 \ge \frac{g}{ R}[/math] and
- [math]\theta = \cos^{-1} \left ( \frac{g}{\omega^2 R} \right ) \equiv \theta_0[/math]
then
- [math]\ddot \theta = \left ( \omega^2 \cos \theta - \frac{g}{R} \right ) \sin \theta [/math]
consider a small displacement from the above angle by and amount \epsilon
- [math] \theta = \theta_0 + \epsilon[/math]
- [math]\cos(\theta_0 + \epsilon) = \cos \theta_0 \cos \epsilon - \sin \theta_0 \sin \epsilon[/math]
- [math]= \cos \theta_0 (1) - \epsilon \sin \theta_0[/math] :: [math]\epsilon[/math] is close to zero
similarly
- [math]\sin(\theta_0 + \epsilon) = \sin \theta_0 \cos \epsilon + \cos \theta_0 \sin \epsilon[/math]
- [math]= \sin \theta_0 (1) + \epsilon \cos \theta_0[/math] :: [math]\epsilon[/math] is close to zero
- [math]\ddot \theta = \left [ \omega^2 \cos \theta - \frac{g}{R} \right ]\sin \theta [/math]
- [math]= \left [ \omega^2 \left ( \cos \theta_0 - \epsilon \sin \theta_0 \right ) - \frac{g}{R} \right ] \left (\sin \theta_0 + \epsilon \cos \theta_0 \right ) [/math]
- [math]= \left [ \left ( \omega^2 \cos \theta_0 - \frac{g}{R}\right ) - \epsilon \omega^2 \sin \theta_0 \right ] \left (\sin \theta_0 + \epsilon \cos \theta_0 \right ) [/math]
but
[math]\left ( \omega^2 \cos \theta_0 - \frac{g}{R}\right ) =0 [/math] given equilibrium condition
- [math]\ddot \theta = \left [ - \epsilon \omega^2 \sin \theta_0 \right ] \left (\sin \theta_0 + \epsilon \cos \theta_0 \right ) [/math]
- [math]= - \epsilon \omega^2 \sin^2 \theta_0 - \epsilon^2 \omega^2 \sin \theta_0 \cos \theta_0 [/math]
- [math]\approx - \epsilon \omega^2 \sin^2 \theta_0 [/math]
- [math]\ddot \theta \approx - \epsilon \omega^2 \sin^2 \theta_0 [/math]
since
- [math] \theta = \theta_0 + \epsilon \Rightarrow \ddot \theta = \ddot \epsilon[/math]
- [math]\ddot \epsilon= - \omega^2 \sin^2 \theta_0 \epsilon = - \omega^{\prime \;2} \epsilon [/math]
- [math]\omega^{\prime \;2} = \sqrt{ \omega^2 \sin^2 \theta_0 } [/math]
- [math] =\omega \sin^ \theta_0 = \omega \sin^ \theta_0 [/math]
- [math] =\omega \sin^ \theta_0 = \omega \sin^ \theta_0 = \sqrt {}[/math]
- [math]\left ( \omega^2 \cos \theta_0 - \frac{g}{R}\right ) =0 [/math] given equilibrium condition
- [math]\sin \theta_0 = \sqrt{1-\cos^2 \theta_0} = \sqrt{1-\left ( \frac{g}{\omega^2 R}\right )^2}[/math]
- [math]\omega^{\prime \;2} = \omega \sqrt{1-\left ( \frac{g}{\omega^2 R}\right )^2} = \sqrt{\omega^2 -\left ( \frac{g}{\omega R}\right )^2}[/math]
Bifurcation
Bifurcation: The splitting of a main body into two parts.
In the example above, as the hoop begins to rotate in the presence of a gravitational field we have one stable equilibrium at the bottom of the hoop. When the hoops rotating frequency reaches a critical value [math]\omega^2 = \frac{g}{ R}[/math] then the bead will be unstable at the bottom and seek to move up the hoop. There are two possible directions equilibrium points on either side of the hoop. The system is said to have bifricated at this point.
http://www-physics.ucsd.edu/students/courses/fall2010/physics110a/LECTURES/CH06.pdf
Forest_Ugrad_ClassicalMechanics
