|
|
| Line 301: |
Line 301: |
| | :<math>f(\phi,\phi^{\prime},\theta) =R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2}(\theta)} d\theta</math> | | :<math>f(\phi,\phi^{\prime},\theta) =R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2}(\theta)} d\theta</math> |
| | | | |
| − | :<math>\frac{\partial f}{\partial \theta} = 0 = \frac{d}{d\theta} \partial{f}{\partial \phi^{\prime}}</math> | + | :<math>\frac{\partial f}{\partial \theta} = 0 = \frac{d}{d\theta} \frac{\partial{f}{\partial \phi^{\prime}}</math> |
| | | | |
| | | | |
Revision as of 15:54, 15 October 2014
Calculus of Variations
Fermat's Principle
Fermats principle is that light takes a path between two points that requires the least amount of time.
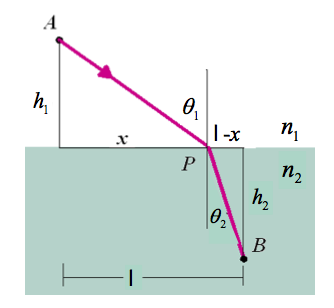
If we let S represent the path of light between two points then
- [math]S=vt[/math]
light takes the time [math]t[/math] to travel between two points can be expressed as
- [math]t = \int_A^B dt =\int_A^B \frac{1}{v} ds [/math]
The index of refraction is denoted as
- [math]n=\frac{c}{v}[/math]
- [math]t = \int_A^B \frac{n}{c} ds [/math]
for light traversing an interface with an nindex of refraction $n_1$ on one side and $n_2$ on the other side we would hav e
- [math]t = \int_A^I \frac{n_1}{c} ds+ \int_I^B \frac{n_2}{c} ds [/math]
- [math]= \frac{n_1}{c}\int_A^I ds+ \frac{n_2}{c} \int_I^B ds [/math]
- [math]= \frac{n_1}{c}\sqrt{h_1^2 + x^2}+ \frac{n_2}{c} \sqrt{h_2^2 + (\ell -x)^2} [/math]
take derivative of time with respect to [math]x[/math] to find a minimum for the time of flight
- [math] \frac{d t}{dx} = 0[/math]
- [math] \Rightarrow 0 = \frac{d}{dx} \left ( \frac{n_1}{c}\left ( h_1^2 + x^2 \right )^{\frac{1}{2}}+ \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{1}{2}} \right )[/math]
- [math] = \frac{n_1}{c}\left( h_1^2 + x^2 \right )^{\frac{-1}{2}} (2x) + \frac{n_2}{c} \left (h_2^2 + (\ell -x)^2 \right)^{\frac{-1}{2}} 2(\ell -x)(-1)[/math]
- [math] = \frac{n_1}{c}\frac{x}{\sqrt{ h_1^2 + x^2 }} + \frac{n_2}{c} \frac{(\ell -x)(-1)}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]
- [math] = n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} - n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]
- [math] \Rightarrow n_1\frac{x}{\sqrt{ h_1^2 + x^2 }} = n_2 \frac{\ell -x}{\sqrt{h_2^2 + (\ell -x)^2}} [/math]
or
- [math] \Rightarrow n_1\sin(\theta_1) = n_2 \sin(\theta_2) [/math]
Generalizing Fermat's principle to determining the shorest path
One can apply Fermat's principle to show that the shortest path between two points is a straight line.
In 2-D one can write the differential path length as
- [math]ds=\sqrt{dx^2+dy^2}[/math]
using chain rule
- [math]dy = \frac{dy}{dx} dx \equiv y^{\prime}(x) dx[/math]
the the path length between two points [math](x_1,y_1)[/math] and [math](x_2,y_2)[/math] is
- [math]S = \int_{(x_1,y_1)}^{(x_2,y_2)} ds= \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+dy^2}[/math]
- [math] = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{dx^2+\left ( y^{\prime}(x) dx\right)^2}[/math]
- [math] = \int_{(x_1,y_1)}^{(x_2,y_2)} \sqrt{1+y^{\prime}(x)^2}dx[/math]
adding up the minimum of the integrand function is one way to minimize the integral ( or path length)
let
- [math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]
the path integral can now be written in terms of dx such that
- [math]S= \int_{(x_1)}^{(x_2)} f(y,y^{\prime},x) dx[/math]
To consider deviation away from [math]y(x)[/math] the function [math]\eta(x)[/math] is introduced to denote deviations away from the shortest line and the parameter [math]\alpha[/math] is introduced to weight that deviation
- [math]\eta(x)[/math] = the difference between the current curve and the shortest path.
let
- [math]Y(x) = y(x) + \alpha \eta(x)[/math] = A path that is not the shortest path between two points.
let
- [math]S(\alpha)= \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx[/math]
the deviations in the various paths can be expressed in terms of a differential of the above integral for the path length with respect to the parameter [math]\alpha[/math] as this parameter changes the deviation
- [math]\frac{\partial}{\partial \alpha} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) = \frac{\partial y}{\partial \alpha}\frac{\partial f}{\partial y}+\frac{\partial y^{\prime}}{\partial \alpha} \frac{\partial f}{\partial y^{\prime}}= \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}}[/math]
- [math]\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} \frac{d}{d \alpha}f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) + \int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx[/math]
The second integral above can by evaluated using integration by parts as
let
- [math]u = \frac{\partial f}{\partial y^{\prime}} \;\;\;\;\;\;\;\;\;\;\;\; dv = \eta^{\prime} dx[/math]
- [math]du = \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \;\;\;\;\;\;\;\;\;\;\;\; v=\eta [/math]
- [math]\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = \left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2} - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]
- [math]\left [ \eta \frac{\partial f}{\partial y^{\prime}} \right ]_{x_1}^{x_2} = \left [ \eta \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2} } \right ]_{x_1}^{x_2} [/math] :[math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]
- [math]= \left ( \eta(x_2) - \eta(x_1) \right ) \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2}} [/math]
- the difference between the end points should be zero because [math]\eta(x_1) = \eta(x_2)[/math] to keep be sure that the endpoints are the same
- [math]\int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx = 0 - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]
- [math]\frac{dS(\alpha)}{d \alpha}=\frac{d}{d \alpha} \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) - \int_{(x_1)}^{(x_2)} \eta \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right )dx [/math]
- [math]= \int_{(x_1)}^{(x_2)} \eta \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] dx [/math]
The above integral is equivalent to
- [math]\int \eta(x) g(x) = 0[/math]
For the above to be true for any function [math]\eta(x)[/math] then it follows that [math]g(x)[/math] should be zero
- [math] \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 [/math]
- [math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]
- [math]\frac{\partial f}{\partial y} = \frac{\partial }{\partial y} \sqrt{1+y^{\prime}(x)^2} = 0 [/math]
- [math] \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) = \frac{d}{dx} \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) = \frac{\partial f}{\partial y} = 0 [/math]
- [math] \Rightarrow \left ( \frac{\partial ( \sqrt{1+y^{\prime}(x)^2})}{\partial y^{\prime}} \right ) [/math]= Constant
- [math] \frac{y^{\prime}(x)}{ \sqrt{1+y^{\prime}(x)^2}} = C [/math]
- [math] \left ( y^{\prime}(x)\right )^2=C^2 \left ( 1+y^{\prime}(x)^2\right ) [/math]
- [math] \left (1 - C^2 \right ) \left ( y^{\prime(x) }\right )^2=C^2 [/math]
- [math] \left ( y^{\prime}(x)\right )^2=\frac{C^2}{1 - C^2) } [/math]
- [math] y^{\prime}(x)=\sqrt{\frac{C^2}{1 - C^2) } } \equiv m[/math]
integrating
- [math]y =mx+b[/math]
http://scipp.ucsc.edu/~haber/ph5B/fermat09.pdf
Euler-Lagrange Equation
The Euler- Lagrange Equation is written as
- [math] \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{dx} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] =0 [/math]
the above becomes a condition for minimizing the "Action"
Problem 6.16
Brachistochrone problem
Shortest distance betwen two points revisited
Let's consider the problem of determining the shortest distance between two points again.
Previously we determined the shortest distance by assuming only two variables. One was the independent variable [math]x[/math] and the other was dependent on [math]x[/math] ([math] y(x)[/math]).
What happens if the above assumption is relaxed.
To consider all possible paths between two point we should write the path in parameteric form
- [math] x=x(u) \;\;\;\;\;\; y = y(u)[/math]
The functions above are assumed to be continuous and have continuous second derivatives.
- Note
- the above parameterization includes our previous assumption of the variables if we just let [math]u=x[/math].
- Other examples
- [math] x=u \;\;\;\;\;\; y = u^2 \;\;\;\;\ \Rightarrow y = x^2 =[/math] parabola
- [math] x=\sin u \;\;\;\;\;\; y = \cos u \;\;\;\;\ \Rightarrow x^2 + y^2 =1 =[/math]circle
- [math] x=a\sin u \;\;\;\;\;\; y = b\cos u \;\;\;\;\ \Rightarrow [/math]ellips
- [math] x=a\sec u \;\;\;\;\;\; y = b\tan u \;\;\;\;\ \Rightarrow [/math]hyperbola
The length of a small segment of the path is given by
- [math]ds = \sqrt{dx^2 + dy^2}= \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2}[/math]
now instead of
- [math]f(y,y^{\prime},x) \equiv \sqrt{1+y^{\prime}(x)^2}[/math]
you have
- [math]f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u) \equiv \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2} [/math]
and the path integral changes from
- [math]S= \int_{(x_1)}^{(x_2)} f(y,y^{\prime},x) dx[/math]
to
- [math]L = \int_{u_1}^{u_2} \sqrt{x^{\prime}(u)^2 + y^{\prime}(u)^2} du =\int_{u_1}^{u_2} f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u)du[/math]
the same arguments are made again
instead of
- [math]Y(x) = y(x) + \alpha \eta(x)[/math]
You now have
- [math] y = y(u) + \alpha \eta(u) \;\;\;\;\;\;\;\; x(u) + \beta \xi(u) [/math]
instead of
- [math]S(\alpha)= \int_{(x_1)}^{(x_2)} f(Y,Y^{\prime},x) dx[/math]
- [math]= \int_{(x_1)}^{(x_2)} f(y+\alpha \eta,y^{\prime}+ \alpha \eta^{\prime},x) dx[/math]
you now have
- [math]S(\alpha,\beta)= \int_{(u_1)}^{(u_2)} f(x(u),y(u),x^{\prime}(u),y^{\prime}(u),u)du[/math]
- [math]= \int_{(u_1)}^{(u_2)} f(x(u) + \beta \xi(u),x^{\prime}(u) + \beta \xi^{\prime}(u),y(u)+\alpha \eta(u),y^{\prime}(u)+ \alpha \eta^{\prime}(u),u) du[/math]
If you require that the integral not deviate from the shortest path between two points (i.e. it is stationary)
Then you are requiring that the integral from path segments that deviate from the shortest path satisfies the equation
- [math]\frac{\partial S}{\partial \alpha} = 0\;\;\;\;[/math] and [math]\;\;\;\;\;\frac{\partial S}{\partial \beta} = 0[/math]
when
- [math]\alpha \mbox{and} \beta = 0[/math] for any function [math]\eta(u)[/math] and [math]\xi(u)[/math] that vanish at the endpoints [math]u_1[/math] and [math]u_2[/math]
- [math]\frac{\partial S(\alpha)}{\partial \alpha}=\frac{\partial}{\partial \alpha} \int_{(u_1)}^{(u_2)} f(x(u) + \beta \xi(u),x^{\prime}(u) + \beta \xi^{\prime}(u),y(u)+\alpha \eta(u),y^{\prime}(u)+ \alpha \eta^{\prime}(u),u) du[/math]
- [math]= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y}+\eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )dx[/math]
- [math]= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) + \int_{(x_1)}^{(x_2)} \left ( \eta^{\prime} \frac{\partial f}{\partial y^{\prime}} \right )du[/math]
- [math]= \int_{(u_1)}^{(u_2)} \left ( \eta \frac{\partial f}{\partial y} \right ) - \int_{(x_1)}^{(x_2)} \eta \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right )du [/math]
- [math]= \int_{(u_1)}^{(u_2)} \eta \left [ \left ( \frac{\partial f}{\partial y} \right ) - \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) \right ] du [/math]
or
- [math] \frac{\partial f}{\partial y} = \frac{d}{du} \left ( \frac{\partial f}{\partial y^{\prime}} \right ) [/math]
similarly
- [math] \frac{\partial f}{\partial x} = \frac{d}{du} \left ( \frac{\partial f}{\partial x^{\prime}} \right ) [/math]
Apply Euler-Lagrange to shortest path problem revisited
- [math]f(x,x^{\prime},y,y^{\prime},u) = \sqrt{x^{\prime\;2}+x^{\prime\;2}}[/math]
- [math]frac{\partial f}{\partial x} = 0 = \frac{d}{du} \partial{f}{\partial x^{\prime}}[/math]
- [math]\Rightarrow \partial{f}{\partial x^{\prime}} = C_1[/math]= constant
- [math]= \frac{x^{\prime}}{\sqrt{x^{\prime\;2}+x^{\prime\;2}}}[/math]
similarly
- [math]C_2= \frac{y^{\prime}}{\sqrt{x^{\prime\;2}+y^{\prime\;2}}}[/math]
- [math]\frac{C_2}{C_1} = \frac{ \frac{y^{\prime}}{\sqrt{x^{\prime\;2}+y^{\prime\;2}}}}{\frac{x^{\prime}}{\sqrt{x^{\prime\;2}+x^{\prime\;2}}}}= \frac{ y^{\prime}}{x^{\prime}} \equiv m[/math]
Shortest path along a sphere
- [math]ds = \sqrt{(Rd\theta)^2+(R\sin \theta d\phi)^2}= R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2(\theta)}} d\theta[/math]
- [math]S=\int_{\theta_1}{\theta_2} R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2}(\theta)} d\theta[/math]
- [math]f(\phi,\phi^{\prime},\theta) =R\sqrt{1+\sin^2 \theta \phi ^{\prime\;2}(\theta)} d\theta[/math]
- [math]\frac{\partial f}{\partial \theta} = 0 = \frac{d}{d\theta} \frac{\partial{f}{\partial \phi^{\prime}}[/math]
- [math]\Rightarrow \frac{\partial f}{\partial \phi^{\prime}} = C[/math]= constant
- [math]= \frac{\sin^2 \phi^{\prime}}{\sqrt{1+\sin^2 \theta \phi^{\prime\;2}}}[/math]
Assume the location of the first point is at [math]\theta_1=0[/math] and [math]\phi = 0[/math]
https://www.fields.utoronto.ca/programs/scientific/12-13/Marsden/FieldsSS2-FinalSlidesJuly2012.pdf
Forest_Ugrad_ClassicalMechanics
