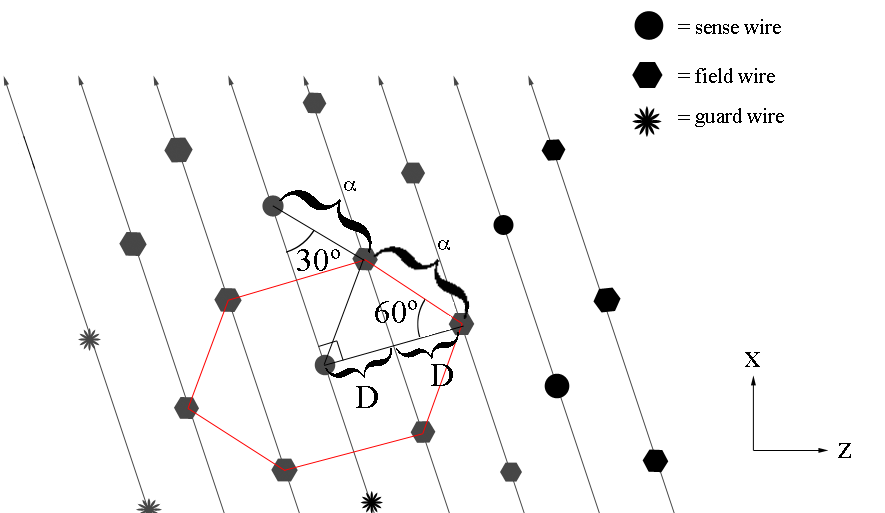
Determining wire-phi correspondance

Detector Geometry

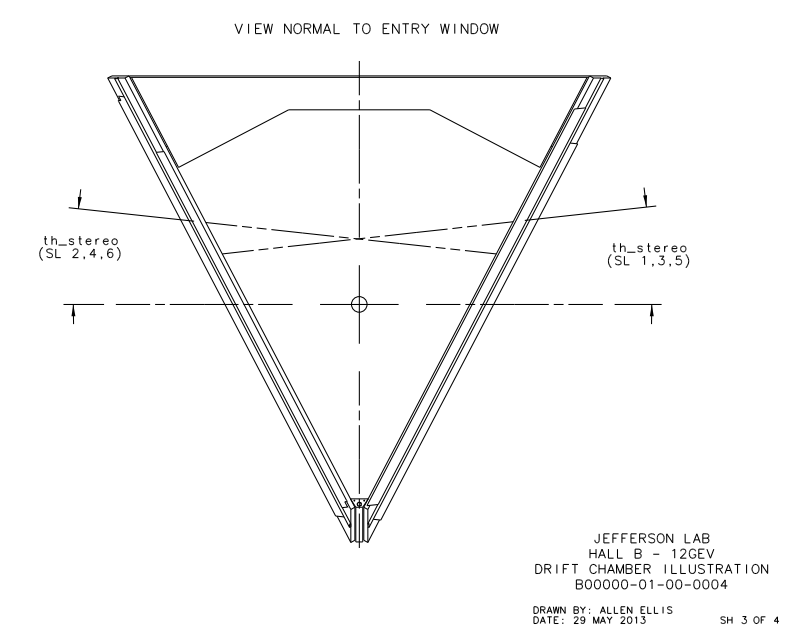
Examining the geometry of the Drift Chamber, we can see that the detector is similar to a hexagonal pyramid in shape.

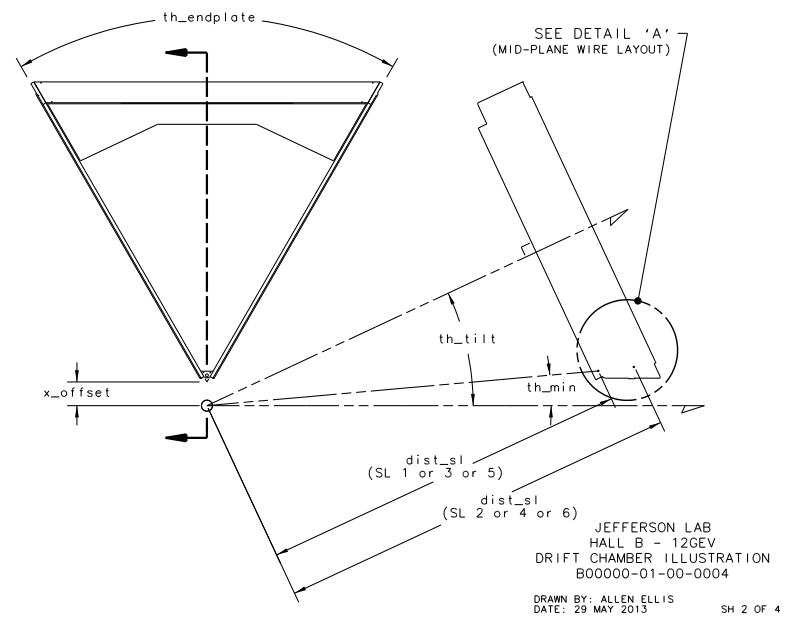
From the geometry it is given that xdist, the distance between the line of intersection of the two end-plate planes and the target position, is equal to 8.298 cm and th_min, the angle from the target vertex to the the same line, is 4.694 degrees. Using this knowledge we can simulate this situation by having the end-plate planes intersect at the beam line axis. This action in effect would grant the sector to measure angles below ~5 degrees, which we can account for by limiting angles theta within the accepted detector range. The quantity dist2tgt, the distance from the target to the first guard wire plane along the normal of said plane, is given as 228.078 cm. Using the previous understanding of the distances between planes within a Superlayer:

We know that the seperation between levels is a constant D=.3861 cm, and that sensor layer 1 is 3 layers deep.

This gives us the distance to level 1 from the vertex (0,0,0) as 228.078 cm+3(0.3861) cm=229.2363 cm in the positive z direction along the beam line. Using the fact that the wire planes are at 25 degrees to the beam line, we can approximate sector one as triangle that intersects with a line perpendicular to the beam line at the vertex position of (0,0,0) along the bisector of the triangle. While this is beyond the physical constructs of the experimental design, we do this mathematical simplicity. This again is acceptable in that angles beyond the physical limitations of 40 degrees will not be simulated. From the geometry of a hexagonal pyramid, we can see that the quantity h should be

[math]h=2.292363\ m\ \cdot Tan(25^{\circ})[/math]

[math]h=1.07\ m[/math]

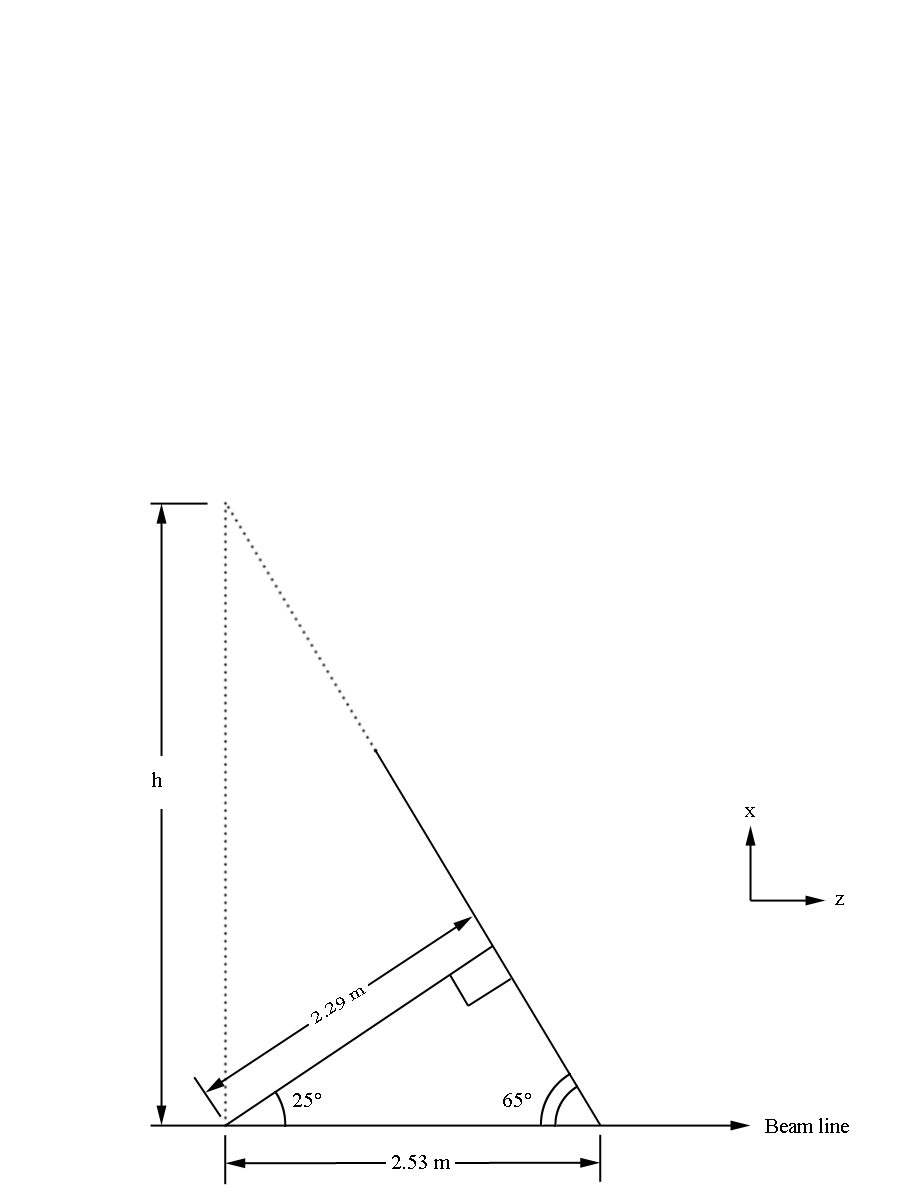
Examining the geometry of a hexagonal of h=[math]\sqrt{3}[/math] whose coordinates are easy to calculate:

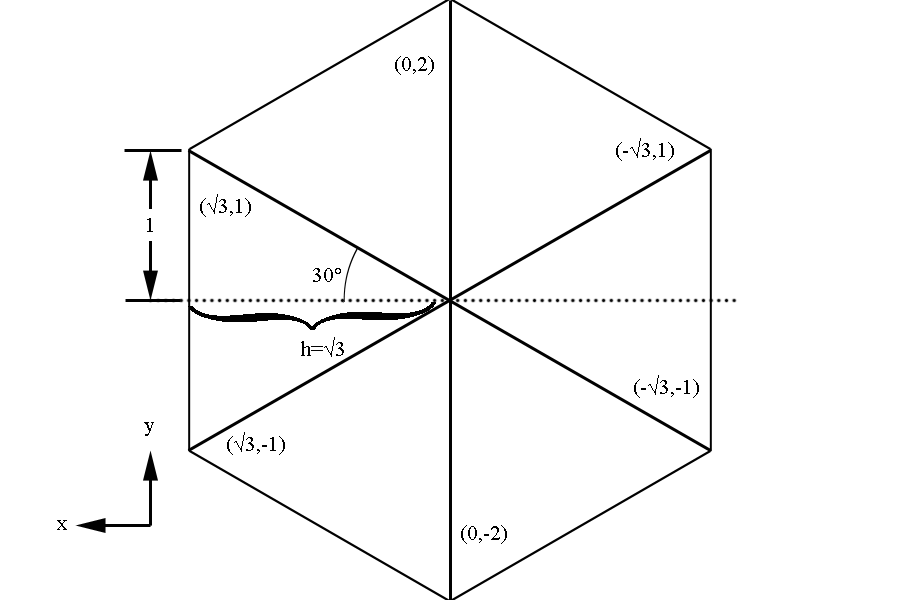
We can scale this hexagon by a factor of .617 to find the base of the hexagonal pyramid simulating the drift chamber geometry.

sector1=Graphics3D[{Red,Opacity[.8],Polygon[{{0,0,2.29},{.617\[Sqrt]3,.617,0},{.617\[Sqrt]3,-.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector2=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{.617\[Sqrt]3,-.617,0},{0,-2*.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector3=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{0,-2*.617,0},{-.617\[Sqrt]3,-.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector4=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{-.617\[Sqrt]3,-.617,0},{-.617\[Sqrt]3,.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector5=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{-.617\[Sqrt]3,.617,0},{0,2*.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
sector6=Graphics3D[{GrayLevel[0.5],Opacity[.2],Polygon[{{0,0,2.29},{0,2*.617,0},{.617\[Sqrt]3,.617,0}}]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];
Bisector0Sector1=Graphics3D[Line[{{0,0,2.29},{.617\[Sqrt]3,0,0}}]];
Bisector0perpSector1=Graphics3D[Line[{{0,0,0},{.617\[Sqrt]3,0,0}}]];
RightAngleVertical=Graphics3D[Line[{{.25,0,.25},{.25,0,0}}]];
RightAngleHorizontal=Graphics3D[Line[{{.25,0,.25},{0,0,.25}}]];
Bisector0Cone=Graphics3D[Line[{{.617\[Sqrt]3,0,0},{.617\[Sqrt]3,0,2.29}}]];
Bisector0perpCone=Graphics3D[Line[{{0,0,2.29},{.617\[Sqrt]3,0,2.29}}]];
RightAngleVertical2=Graphics3D[Line[{{.617\[Sqrt]3-.25,0,2.29-.25},{.617\[Sqrt]3-.25,0,2.29}}]];
RightAngleHorizontal2=Graphics3D[Line[{{.617\[Sqrt]3-.25,0,2.29-.25},{.617\[Sqrt]3,0,2.29-.25}}]];
BeamLine=Graphics3D[Arrow[{{0,0,-.5},{0,0,2.79}}]];
PhiCone=Graphics3D[{Blue,Opacity[.3],Cone[{{0,0,2.29},{0,0,0}},.617\[Sqrt]3]},BoxStyle->Dashing[{0.02,0.02}],Axes->True,AxesLabel->{"x","y","z"},Ticks->None,AxesStyle->Thickness[0.01]];

Viewing the simulation,

Show[sector1,sector2,sector3,sector4,sector5,sector6,PhiCone,BeamLine,Bisector0Sector1,Bisector0perpSector1,Bisector0Cone,Bisector0perpCone,RightAngleVertical,RightAngleHorizontal,RightAngleVertical2,RightAngleHorizontal2]

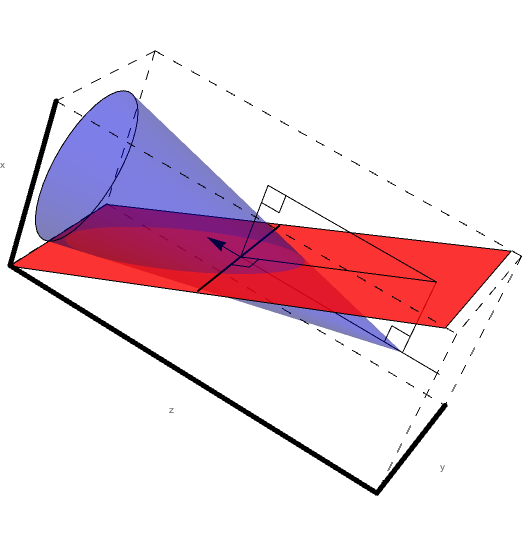
When the scattering angle theta, which is measured with respect to the beam line, is held constant and rotated through 360 degrees in phi, a cone is created. Using Mathematica, we can produce a 3D rendering of how the sectors for Level 1 would have to interact with a steady angle theta with respect to the beam line, as angle phi is rotated through 360 degrees.

Conic Sections

Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.

Show[sector1,PhiCone,BeamLine,Bisector0Sector1,Bisector0perpSector1,Bisector0Cone,Bisector0perpCone,RightAngleVertical,RightAngleHorizontal,RightAngleVertical2,RightAngleHorizontal2]

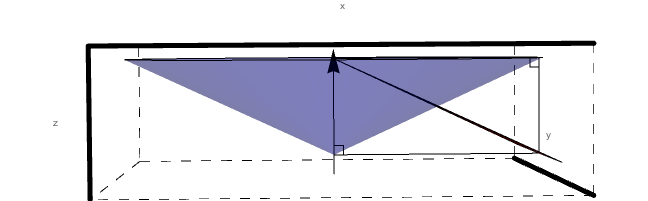
Without loss of generalization, we can extend the triangle to an infinite plane to aid in viewing the conic section. Again, this falls outside of the experimental design range, but simulations would not occur in this forbidden zone.

sector1plane = 
  Graphics3D[{Red, Opacity[.8], 
    InfinitePlane[{{0, 0, 2.29}, {.617 \[Sqrt]3, .617, 
       0}, {.617 \[Sqrt]3, -.617, 0}}]}, 
   BoxStyle -> Dashing[{0.02, 0.02}], Axes -> True, 
   AxesLabel -> {"x", "y", "z"}, Ticks -> None, 
   AxesStyle -> Thickness[0.01]];

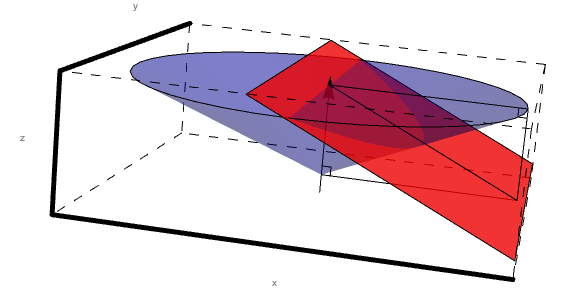
Following the rules of conic sections we know that the eccentricity of the conic is given by:

[math]e=\frac{\sin \beta}{\sin\alpha}[/math]

where β is the angle between the plane and the horizontal and α is the angle between the cone's slant generator and the horizontal.

Examining the different conic sections possible we know that:

Circular Conic Section

If the conic is an circle, e=0. This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}=0[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{0}=cos( \theta) =\infty[/math]

The sector angle will never be perpendicular to the plane of the light cone, so this is not a physical possibility.

Elliptic Conic Section

If the conic is an ellipse, 0<e<1. This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{cos (\theta)}=e[/math]

since e must be less than 1, this sets the limit of theta at less than 25 degrees. Similarly, since the limit of theta observed is 0 degrees, this sets the lower limit for the eccentricity

[math]\frac{cos (25^{\circ})}{cos (0)}=e=.9063078[/math]

This implies that the shape made on the the plane of the sector is an ellipse for angles

[math] 0\lt \theta\lt 25^{\circ}[/math]

Determining ellipse components

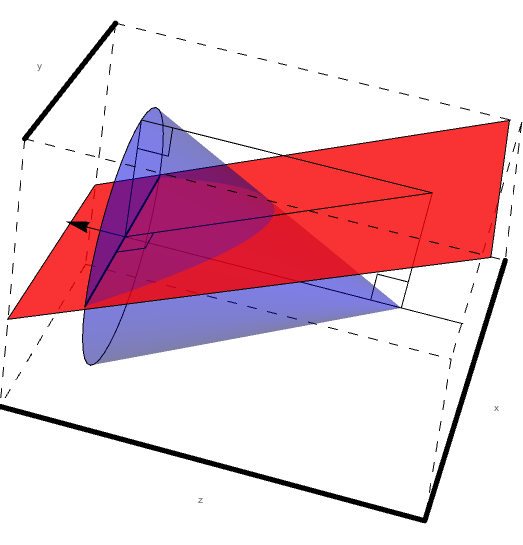
Here we must take note of the fact that the center of the cone and the center of the ellipse do not coincide as can be shown visually by extending the cone length.

Viewing the xz plane

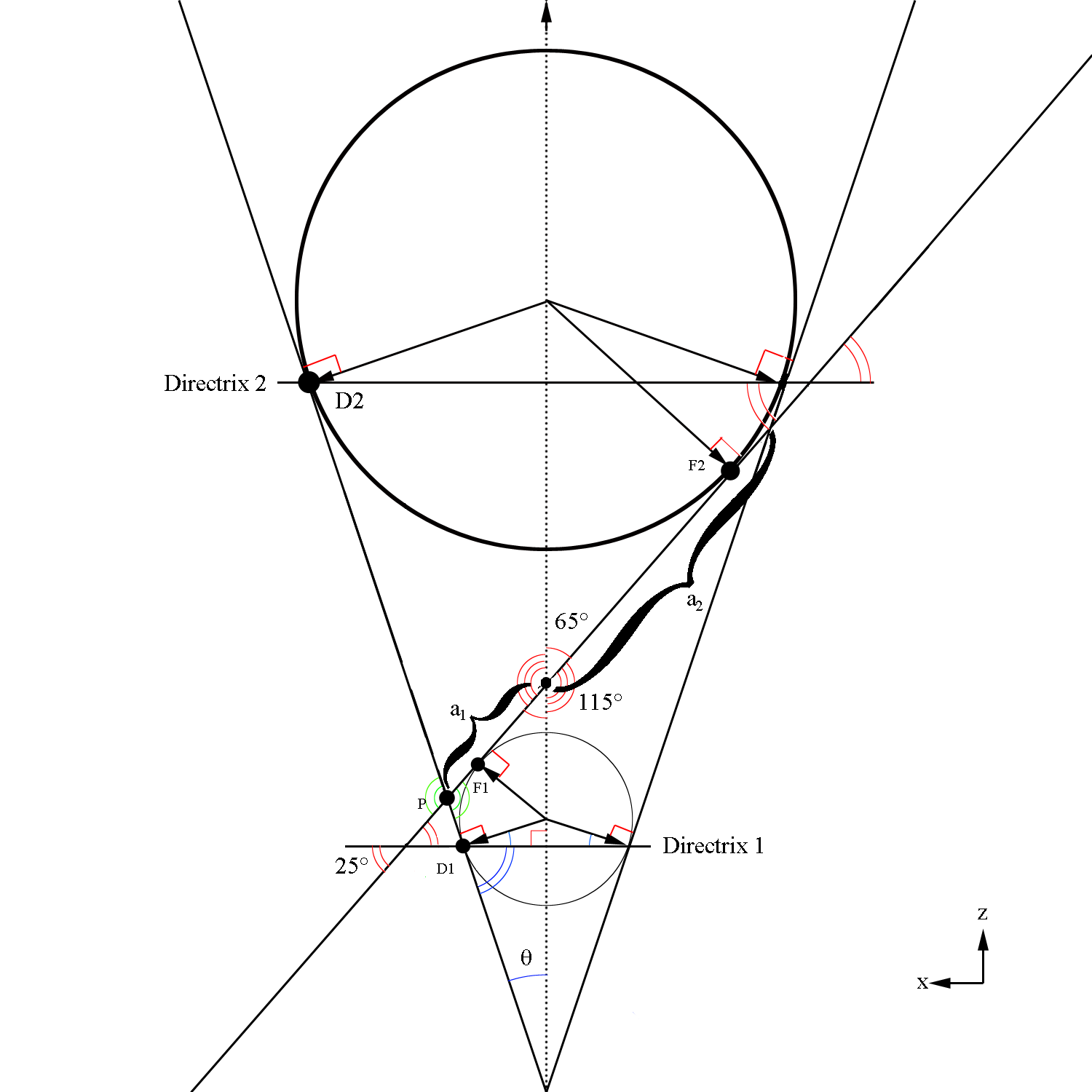
We can use the law of sines to find a portion of the ellipse

[math]\frac{a}{sin(A)}=\frac{b}{sin(B)}[/math]

[math]\frac{2.29\ m}{sin(155^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]

[math]\frac{a}{sin(A)}=\frac{b}{sin(B)}[/math]

[math]\frac{2.29\ m}{sin(25^{\circ}-\theta)}=\frac{a_2}{sin(\theta)}[/math]

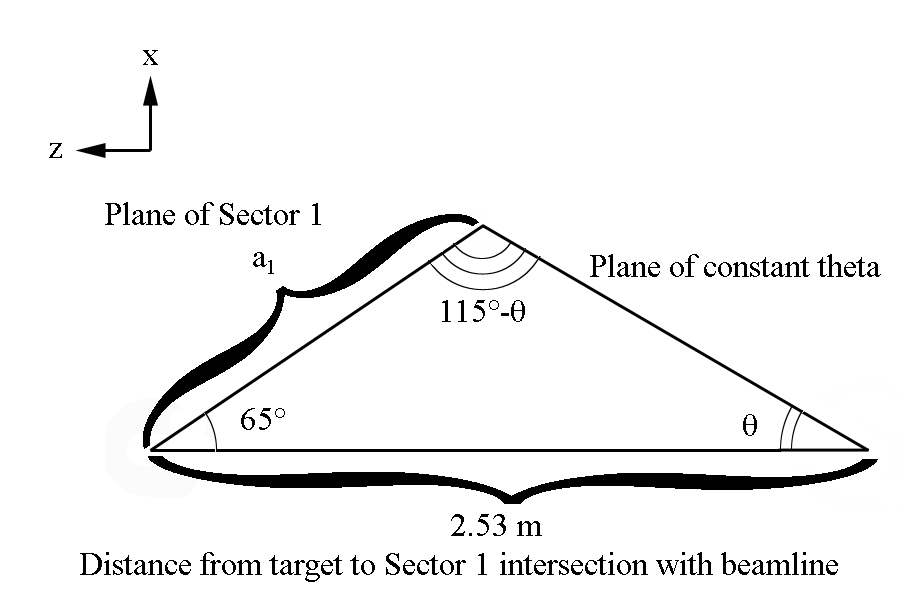
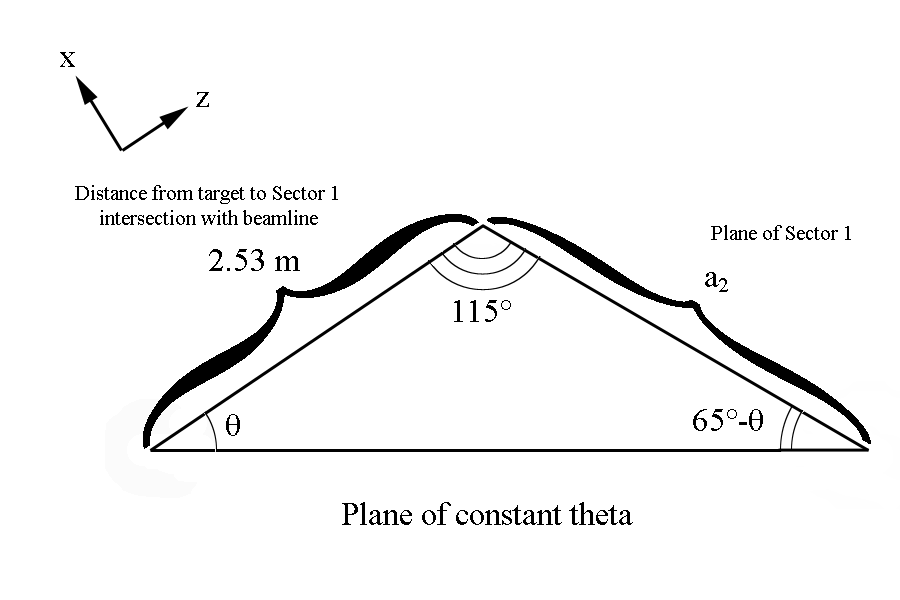
Since these lines meet at theintersection of each other, and they both originate at the vertex positions for the ellipse, we can state that the semi major axis is:

[math]2a=a_1+a_2[/math]

Using the fact that half the semi-major axis will give use the center of the ellipse

[math]a=\frac{a_1+a_2}{2}[/math]

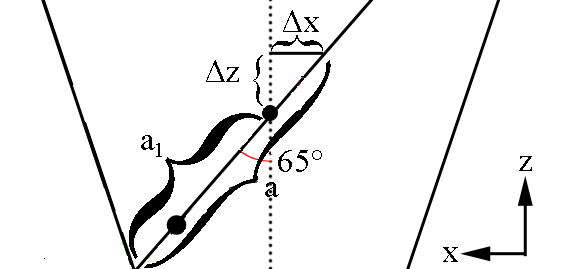
Earlier, using the law of sines it was found:

[math]\frac{2.29\ m}{sin(155^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]

[math]\frac{2.29\ m \cdot sin(\theta)}{sin(155^{\circ}-\theta)}=a_1[/math]

Taking the difference

[math]\Delta a=a-a_1=\frac{a_1+a_2}{2}-a_1=\frac{a_2-a_1}{2}[/math]

[math]\Delta z=\Delta a \cdot cos(25^{\circ})[/math]

[math]\Delta x=\Delta a \cdot sin(25^{\circ})[/math]

The cone at this z distance has a radius of

[math]r\equiv b=2.29\ m+\Delta z \cdot sin(\theta)[/math]

A property of an ellipse is that the two lines from the focii to the same point on the ellipse's surface sum to a constant

[math][[Ellipse_sum_rule.png\lt /center\gt \lt center\gt \lt math\gt PF1+PF2=2a[/math]

Since the vertex position is at (0,0,0) this shows the center of the ellipse to be at [math](-\Delta a, 0,z+\Delta z)[/math]

Determining Elliptical Equation

For ellipses centered at (h,k) in the plane of the ellipse:

[math]\frac{(x^{'}-h)^2}{a^2}+\frac{(y^{'}-k)^2}{b^2}=1[/math]

where

[math]a = major\ radius\ (= \frac{1}{2}\ length\ major\ axis)[/math] [math]b = minor\ radius\ (= \frac{1}{2}\ length\ minor\ axis)[/math]

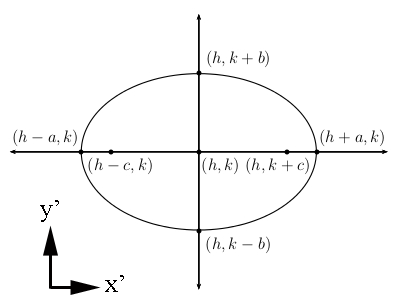
Where the distance from the center of the ellipse to a focal point is found by:

[math]c^2\equiv a^2-b^2[/math]

As found earlier

[math]\theta\equiv 4.49876 +0.293001 n+0.000679074 n^2-3.57132\times 10^{-6} n^3[/math]

As discussed earlier, taking the 1st derivative of this function will give us the spacing of the bins as a function of wire number.

[math]\theta '\equiv 0.293001 + 0.00135815 n - 0.000010714 n^2[/math]

Parabolic Conic Section

If the conic is an parabola, e=1

This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\alpha)}=1[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{1}=cos (\theta) [/math] [math]\theta=25^{\circ}[/math]

For a parabola:

[math]4px = y^2[/math]

where

p = distance from vertex to focus (or directrix)

Hyperbolic Conic Section

If the conic is an hyperbola, e>1

This implies

[math]e=\frac{\sin \beta}{\sin \alpha}=\frac{\sin\ (90^{\circ}-25^{\circ})}{\sin (90^{\circ}-\theta)}\gt 1[/math]

Using the identity

[math]sin(90^{\circ}-t)=cos(t)[/math]

[math]\frac{cos (25^{\circ})}{1}\gt cos (\theta) [/math]

[math]\theta\gt 25^{\circ}[/math]

Additionally, since the dector has an upward limit of 40 degres this implies that

[math]25^{\circ}\gt \theta\gt 40^{\circ}[/math]