[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Determining ellipse components
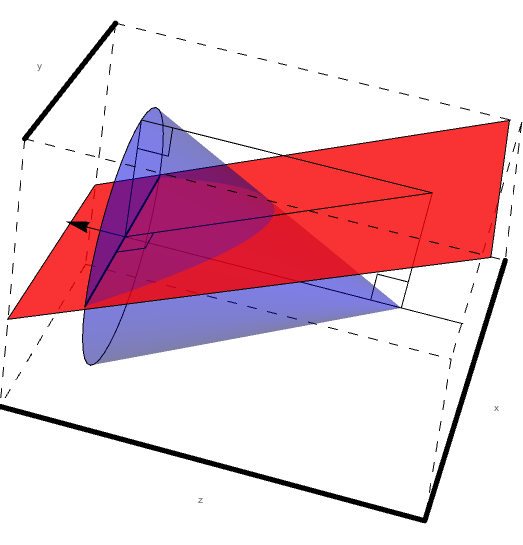
Figure 5: A cone of constant Theta with varying Phi.
Here we must take note of the fact that the center of the cone and the center of the ellipse do not coincide as can be shown visually by extending the cone length.
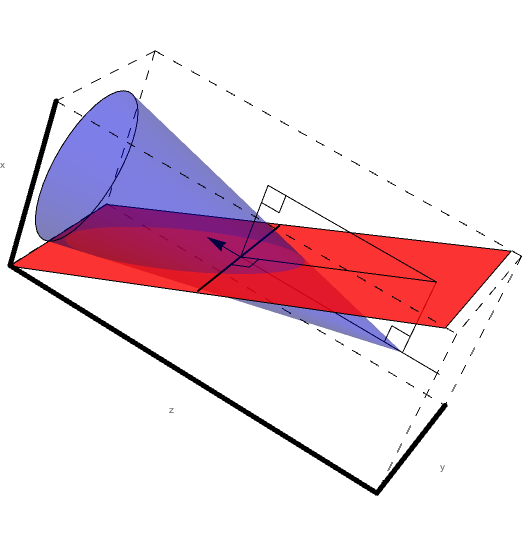
Figure 5: A cone of constant Theta with varying Phi.
Here we will make use of Dandelin spheres to help determine the ellipse components with reference to the cone created at a constant theta. The basic construction of using Dandelin spheres is that within the cone, there are two spheres which are tangent to the plane as well as tangent to the cone as shown below in the xz plane. The Dandelin method picks an arbitrary point,P, on the intersection of the cone and the ellipse's plane. Drawing a line from the cone vertex through the point P, the directrix lines are intersected as shown below at D1 and D2. From the geometry as shown in the xz plane, it is shown that the line segments F1P=D1P and F2P=D2P since they share a common line segment, all three angles, and both have a the respective Dandelin radius as parts of the triangles they form.
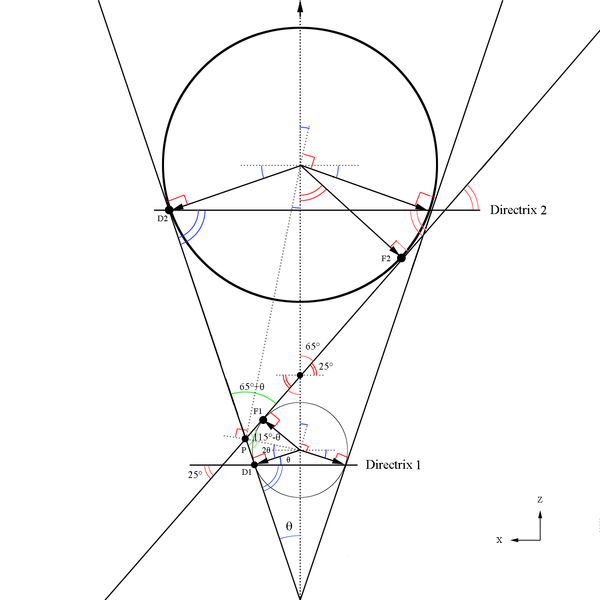
Figure 5: A cone of constant Theta with varying Phi.
We can use the law of sines to find a portion of the ellipse
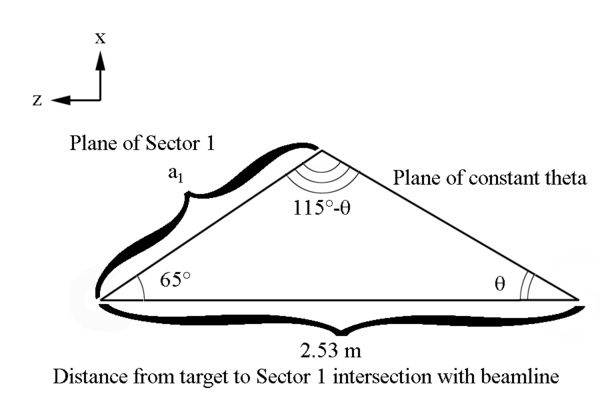
Figure 5: A cone of constant Theta with varying Phi.
[math]\frac{2.53\ m}{sin(115^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]
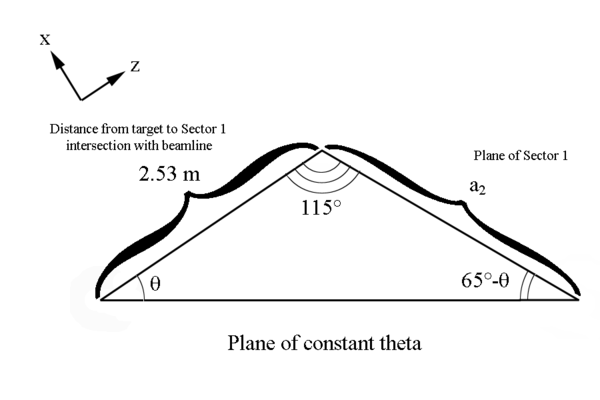
Figure 5: A cone of constant Theta with varying Phi.
[math]\frac{a}{sin(A)}=\frac{b}{sin(B)}[/math]
[math]\frac{2.53\ m}{sin(65^{\circ}-\theta)}=\frac{a_2}{sin(\theta)}[/math]
Since these lines meet at the intersection of each other, and they both originate at the vertex positions for the ellipse, we can state that the semi major axis is:
[math]2a\equiv a_1+a_2[/math]
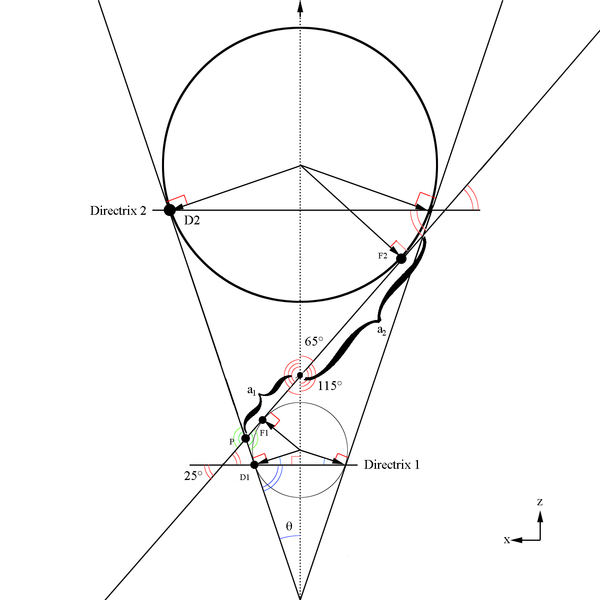
Figure 5: A cone of constant Theta with varying Phi.
Using the fact that half the semi-major axis will give use the center of the ellipse
[math]a=\frac{a_1+a_2}{2}[/math]
[math]a=\frac{2.53sin(\theta)}{2}\left (\frac{sin(115^{\circ}-\theta)+sin(65^{\circ}-\theta)}{sin(115^{\circ}-\theta)sin(65^{\circ}-\theta)}\right )[/math]
[math]a=\frac{2.53sin(\theta)}{2}\left (sin(115^{\circ}-\theta)+sin(65^{\circ}-\theta)\right ) csc(115^{\circ}-\theta)csc(65^{\circ}-\theta)[/math]
| [math]a=\frac{2.53sin(\theta)}{2}\left (csc(65^{\circ}-\theta)+csc(115^{\circ}-\theta) \right )[/math]
|
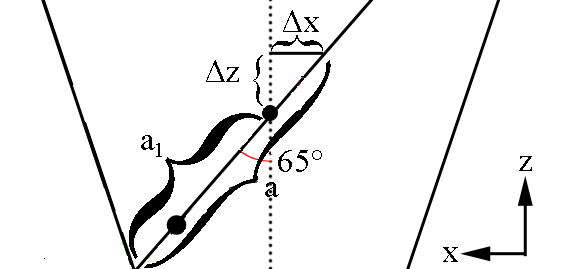
Figure 5: A cone of constant Theta with varying Phi.
Earlier, using the law of sines it was found:
[math]\frac{2.53\ m}{sin(115^{\circ}-\theta)}=\frac{a_1}{sin(\theta)}[/math]
[math]\frac{2.53\ m \cdot sin(\theta)}{sin(115^{\circ}-\theta)}=a_1[/math]
Taking the difference
[math]\Delta a=a-a_1=\frac{a_1+a_2}{2}-a_1=\frac{a_2-a_1}{2}[/math]
| [math]\Delta a=\frac{2.53sin(\theta)}{2}\left (csc(65^{\circ}-\theta)-csc(115^{\circ}-\theta) \right )[/math]
|
[math]\Delta z=\Delta a \cdot cos(65^{\circ})[/math]
[math]\Delta x=\Delta a \cdot sin(65^{\circ})[/math]
Since the vertex position is at (0,0,0) this shows the center of the ellipse to be at
[math]c_{ellipse} \equiv (-\Delta a sin(65^{\circ}), 0,z+\Delta z)[/math]
[math]c_{ellipse} \equiv (-\Delta a sin(65^{\circ}), 0,2.53+\Delta z)[/math]
The sum of the distance from both focal points to a point on the surface of the ellipse is a constant
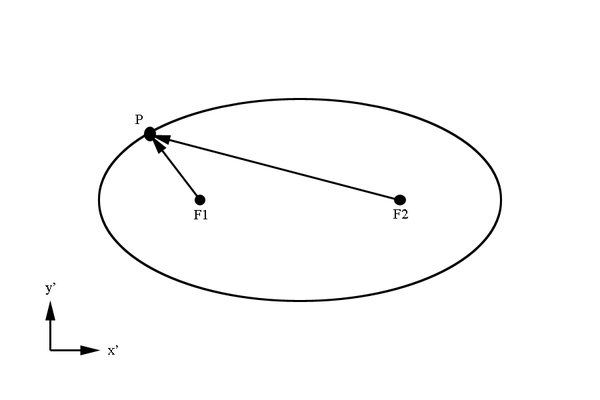
Figure 5: A cone of constant Theta with varying Phi.
A property of an ellipse is that the distance from the center of the ellipse to a focal point is given by
[math]f=ae=\left (\frac{a_1+a_2}{2}\right ) \left ( \frac{sin(25^{\circ})}{cos(\theta)}\right )[/math]
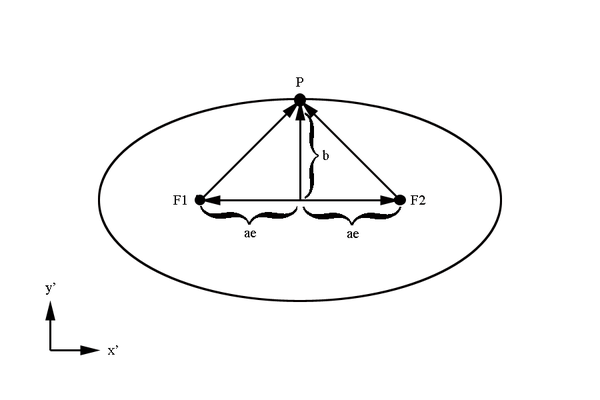
Figure 5: A cone of constant Theta with varying Phi.
[math](ae)^2+b^2=a^2\Rightarrow b=a\sqrt{1-e^2}[/math]
[math]b=\left (\frac{a_1+a_2}{2}\right ) \sqrt{1-\frac{sin(25^{\circ})^2}{cos(\theta)^2} }[/math]
[math]b=\frac{2.53sin(\theta)}{2}\left (\frac{sin(115^{\circ}-\theta)+sin(65^{\circ}-\theta)}{sin(115^{\circ}-\theta)sin(65^{\circ}-\theta)}\right ) \sqrt{1-\frac{sin(25^{\circ})^2}{cos(\theta)^2} }[/math]
Additionally, using the fact that the distance from the center to a focal point is ae
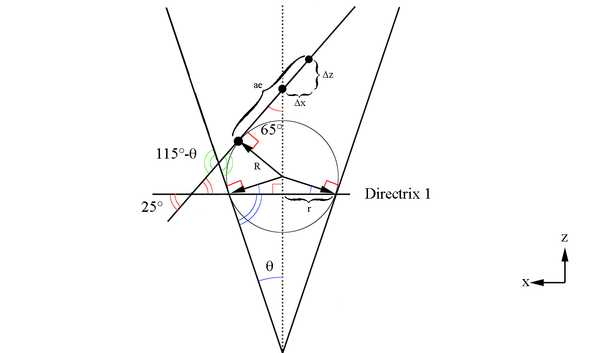
Figure 5: A cone of constant Theta with varying Phi.
[math]R_{Lower\ Dandelin}=(ae-\Delta a) tan(65^{\circ})[/math]
[math]r_{D1}=R_{Lower\ Dandelin}sec(\theta)=(ae-\Delta a) tan(65^{\circ})cos(\theta)[/math]
By symmetry,
[math]R_{Upper\ Dandelin}=(ae+\Delta a) tan(65^{\circ})[/math]
[math]r_{D2}=R_{Lower\ Dandelin}sec(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
==
[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]









