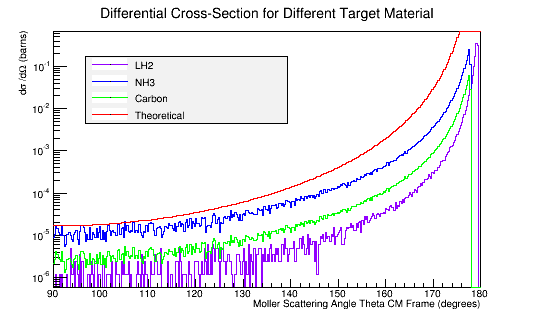
Calculating the differential cross-sections for the different materials, and placing them as well as the theoretical differential cross-section into a plot:
| Material | Density (g/cm3) |
|---|---|
| C | 2.26 |
| NH3 | 0.86 |
| LH2 | 0.07 |
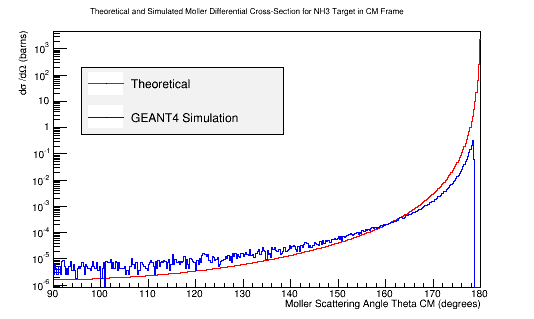
Comparing this to the theoretical differential cross section
As shown earlier , we find that the differential cross section scale is
Converting the number of electrons to barns,
where ρtarget is the density of the target material, ltarget is the length of the target, and iscattered is the number of incident particles scattered.
For LH2:
For Carbon:
For Ammonia:
Combing plots in Root:
new TBrowser();
TH1F *LH2=new TH1F("LH2","LH2",360,90,180);
LH2->Add(MollerThetaCM,1.19e-6);
LH2->Draw();
TH1F *C12=new TH1F("C12","C12",360,90,180);
C12->Add(MollerThetaCM,2.21e-7);
C12->Draw();
TH1F *NH3=new TH1F("NH3","NH3",360,90,180);
NH3->Add(MollerThetaCM,8.87e-7);
NH3->Draw();
LH2->Draw("same");
C12->Draw("same");
Theory->Draw("same");
| Material | Molar Mass (g/mole) |
|---|---|
| NH3 | 17 |
| C | 12 |
| LH2 | 2 |
| Material | Number of Electrons |
|---|---|
| NH3 | 10 |
| C | 6 |
| LH2 | 2 |
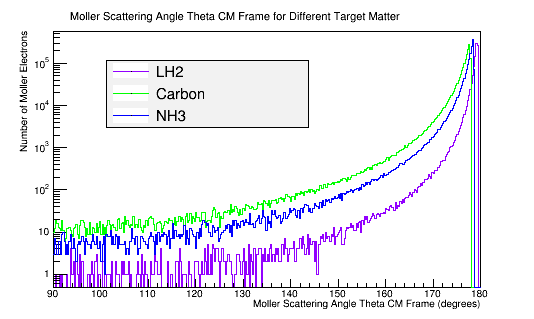
The molar mass is proportional to the number of electrons in the target material. The theoretical Moller differential cross-section is an expression for a single scattering electron. NH3, as a molecule, is composed of 10 electrons that all have an equal momentum and probability of scattering with the incident electron in the CM frame.
Comparing this with a plot of the Moller scattering angle theta,
| Material | Density (g/cm3) |
|---|---|
| C | 2.26 |
| NH3 | 0.86 |
| LH2 | 0.07 |
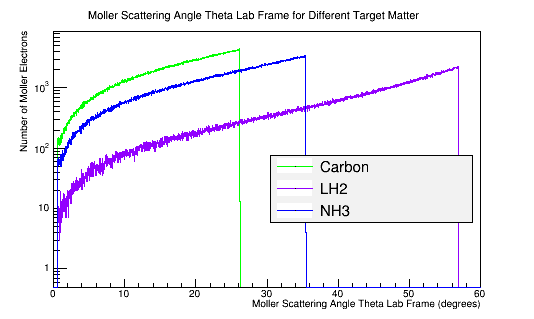
In the lab frame, the incident electron, and the transfer of its momentum, depends on the stationary target material density. The more dense material requires more energy to break free an electron from the target material. This higher energy results in a smaller maximum scattering angle theta for the Moller electron in the Lab frame.
Adjusting the theoretical differential cross-section for 10 times less,
TH1F *Combo=new TH1F("TheoryExperiment","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
TH1F *Combo2=new TH1F("TheoryExperiment2","Theoretical and Experimental Differential Cross-Section CM Frame",360,90,180);
Combo->Add(MollerThetaCM,8.87e-7);
Combo2->Add(Theory,1e-1);
Combo2->Draw();
Combo->Draw("same");