Alpha Ionization

Energy threshold for electron and gamma entering detector

Detemine the energy threshold that an electron and a photon need to surpass in order to pass through the kapton, gas, the copper cathode, and the FR4.

Draw a picture with dimensions of all the layers

Energy -vs- counts per incident particle

Photon and electron Energy -vs- distance through the detector

energy straggling plot at the point where particle just makes it through the detector

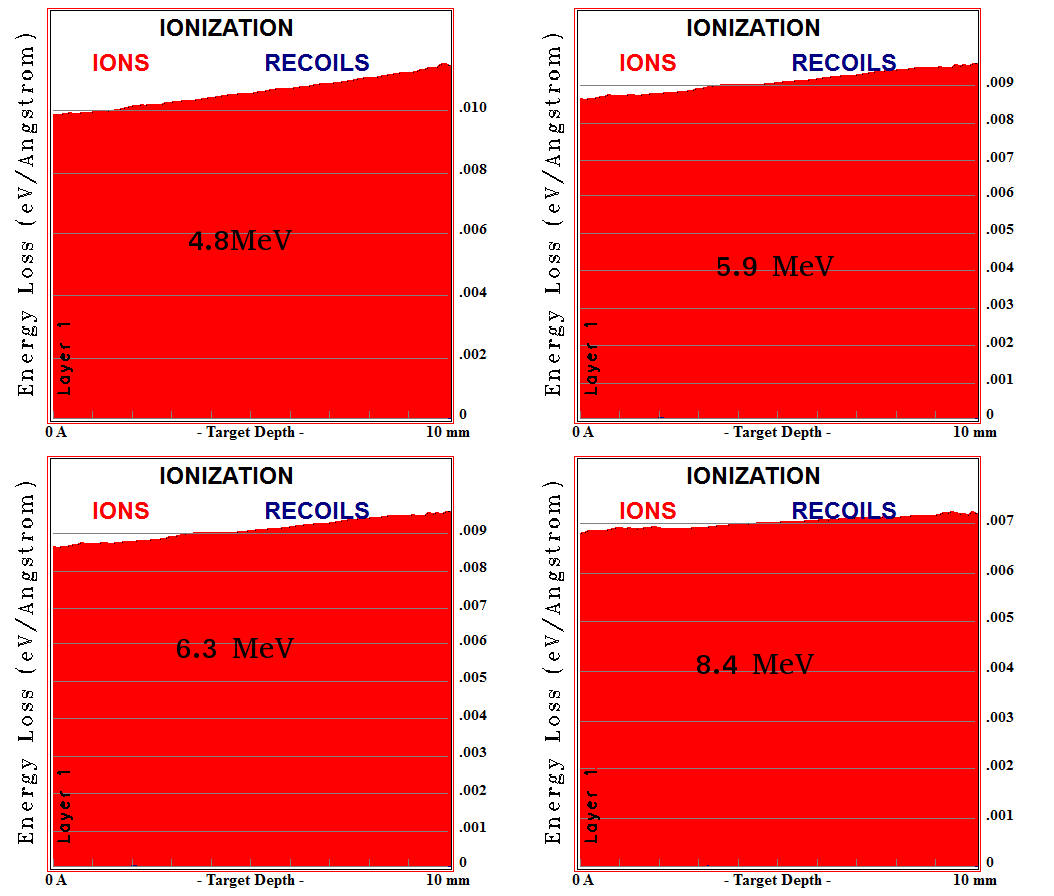
Alpha Particles ionization simulation using GEANT4

GEANT4 simulates the ionization of alpha particles in Ar/CO2 90/10 gas. Geant4 can simulate the ionization process for alpha particles. Unfortunately the value of the step function underestimates the number of delta electrons even after decreasing the step cut to 1 nm. Also,using GEANT4 overestimates the range of alpha particles in Ar/CO2 gas when compared to those that srim calculates File:Alpha range ArCo2.txt, the following table shows the maximum range of alpha particles that are emitted from the U-233, and the ranges calculated by srim.

Alpha Energy (MeV)	G4 Range (cm)	Srim Range (um)
1.0	0.56599	129.49
2.0	1.1467	255.91
3.0	1.9024	417.27
4.0	2.8012	612.45
5.0	3.8425	839.91

Based on the previous table, GEANT4 failed to calculate the expected alpha range for most alpha energies, and underestimated the number of alpha's delta electrons emitted through that range, but it is still useful tool to simulate the primary delta electrons when negative beta particles pass through a defined medium.

Alpha propagation through the drift area with 600V drift voltage

U-233 is an alpha-emitter source, alpha particles at least 4.85 MeV as kinetic energy when they leave the nucleus. The voltage needed to stop an alpha of an energy of 4.85 MeV can be calculated as the following:

[math] K.E_{alpha} = P.E_{drift} = q \times V[/math] where V is the applied voltage.

for an alpha K.E = 4.85 MeV , q = 2e, so:

[math] 4.85 \times 10^6 \times e = 2e \times V [/math]

[math] V = \frac{4.85 \times 10^6}{2} [/math]

[math] V = 2.425 \times 10^6 V [/math]

Compared to the drift voltage, the drift voltage effect is negligible, since the magnitude of work applied against each alpha is just 1.2 keV as shown below:

[math] W = q \times V [/math]

[math] W = 2e * 1100 [/math]

[math] W = 2.2 keV [/math]

Calculating the number of the delta electrons without using GEANT4

There is another way to calculate the number of delta electrons without using GEANT4. It starts by calculating the average energy loss [math] \Delta E_a[/math] by the alpha particles and the average energy loss per unit length [math] {\zeta} [/math] in Ar/CO2 gas using the Bethe-Block equation. It then uses the the following equation:

[math] \lambda = \frac{ \Delta E - \Delta E_a}{\zeta} [/math]

to calculate the actual energy loss by ionization [math] \Delta E [/math], where [math] \lambda [/math] represents random landau number.

By dividing the energy loss by the minimum energy for producing a pair of ion/electron pair W, this equation yields the number of electrons emitted by ionization.

Srim can simulate the motion of an alpha particle in Ar/CO2 gas by allowing for the change in the stopping power per unit length. It can also show the ionization energy loss as shown in the following figure:

This figure shows the ionization energy loss of 999 alpha particles as they pass through Ar/CO2 gas. Integrating the area under the curve and dividing by (W*1000) will estimate the number of delta electrons produced by an alpha particle.

Bethe block formula calculates the average ionization energy loss as the following: [math]- \frac{dE}{dx} = \frac{4 \pi}{m_e c^2} \cdot \frac{nz^2}{\beta^2} \cdot \left(\frac{e^2}{4\pi\varepsilon_0}\right)^2 \cdot \left[\ln \left(\frac{2m_e c^2 \beta^2}{I \cdot (1-\beta^2)}\right) - \beta^2\right][/math]

for an electron of rest mass [math] m_ec^2 = 0.511 MeV [/math], and [math] m_{\alpha}c^2 = 3.727 MeV [/math]

Number of Primary ionization events per cm

Inside the chamber

The figures show the threshold energy for photons traveling in the detector and the number of the absorbed photons within the detector's drift area. Photons travel through the drift area and primarily interact by photoelectric effect with the gas's atoms and molecules; a photon's energy may increase up to 1.1 MeV and still the most probable interaction with the medium is the photoelectric effect. Figure xx1 shows the same numbers of primary electrons produced by an incident photon simulation by GEANT4; once when all photon's interactions are considered (red), and once when only the photoelectric effect only considered (blue). It also shows that all the photons are absorbed by Ar/CO2 gaseous medium. Since the incident photon energy varies from 10 keV up to 1.1 MeV, only the absorbed photons within a 1 cm will affect the detector signal. GEANT4 simulation shows that the dominant interaction is the photoelectric effect even if the incident photon energy reaches 1.1 MeV, and that 25 percent of the photons will be absorbed when their energy is 25 keV, as the energy increases the number of photons decreases to reach 0.03 when the photon energy is 96.1 keV. As a result, gamma energy, emitted by U-233 or bremsstrahlung radiation that appears when the lineac is in operation, should have a maximum energy of 96.1 keV as it is in the detector's drift area, which maximizes the effect on the detector's signal.

7cm Outside the chamber

Photons may reach the detector's drift area and affect its signal when they pass through the kapton window or (less probably) through the ertalyte plastic. Normally, the detector structure is built from materials that prevent the photons of specific energies from causing ionization in the drift area. Figure xx3 shows the incident photon energy at a 7 cm distance from the kapton window and the number of photons absorbed in the drift area that cause ionization by photoelectric effect.

The figure shows a maximum number of absorbed photons; when the incident photon energy is 60 keV, 46 percent of the photons get absorbed by the drift region.

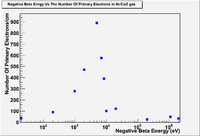
from beta particle as a function of beta particle energy using Garfield and GEANT4

GEANT4 can simulate the primary number of delta electrons for a negative beta particle penetrating ArCO2. Using the TestEm10 example and choosing the appropriate default cut, GEANT4 counts the same number of primary delta electrons for negative beta particles with 1.1 MeV energy, and determines the energy and the momentum of the delta electrons depending on Moller or Bhabha's scattering, and depending on the value of the kinetic energy cut used.<ref name = "Urban">Urbán, L. (1998, 10 09). Geant4 physics reference manual. Retrieved from http: //geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/node41.html </ref>

The following figure shows Garfield simulation for the number of electrons that are collected in the drift region when the shutter is open and as the electron passes a 90/10 Ar/CO2 gas:

Overlay with dE/dx formula and fill in gaps

something is wrong with G4 result for electron energies below 1 keV.

from photon as a function of photon particle energy using Garfield and GEANT4

Chamber Geometry in GEANT4

The chamber geometry for the GEM chamber is set for Calculating the created charge in the detector's drift area is shown below:

Charge particles and photons primary ionization

The physical interactions that take place inside the detector are simulated by GEANT4.9.6 to estimate the primary charge collected by the drift electric field in GEM detector. GEM detector depends mainly on the particles’ interaction with Ar/CO2 atoms and molecules, especially those that directly (or indirectly) produce free charge that can be collected by the drift electric field. Specifically in the GEM detector described by section XX, the detector signal can be produced by gamma rays, electrons, or neutrons. GEANT4.9.6 has been used to estimate the primary charge caused by those particles in case of electrons and neutrons, but for photons, GENAT4 is used to produce the photoionization energy spectrum for Ar/CO2 gas.

The simulation started by determining the number of primary electrons produced by charged particles in Ar/CO2. The number of primary electrons depends on the particles’ charge and mass and kinetic energy. As a result, alpha particles have the highest number of primary electrons, electrons have less primary electrons, and photons have the least number of primary electrons produced per photon, assuming that photoabsorption is the dominant process in Ar/CO2 gas for an energy range of 1 to 300eV.

By modifying EmTest10 example in GEANT4.9.6, the number of primary electrons produced by an electron travels 1 cm is shown in the figure below:

The figure also shows Garfield simulation for an electron's primary ionization; it is noticed that the GEANT4.9.6 results match those of Garfield when the minimum incident electron energy is [math] 2x10^4[/math]eV. Such an energy value is much lower than the threshold kinetic energy which an electron needs to make ionizations in the detector's drift region, since the threshold kinetic energy for an electron is more than 2 MeV 5cm away from the detector's window.

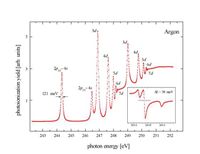
GEANT4.9.6 predicts the number of the primary electrons for a photon. Photon ionization has the least number of electrons, even producing an free electron is constrained to the electronic structure of Ar/CO2 gas.

GENAT4.9.6 does not predict the Argon photoabsorption spectrum specifically for each energy as shown above, the photon energy may have [math] \pm 1[/math]eV shift. It is worth to mention if the photon is not in the drift region, then the detector is completely blind for any photon of energy of 20-300 eV (their range in fm). In case of a 50 keV photon or more, the photon will easily pass the detector chamber without affecting its medium if only photoionization is considered, within that energy range Compton scattering cross section increases, it will produce an electron and a photon in the drift region that can easily be detected. Being in am accelerator environment, photon interaction becomes dominant by Compton Scattering interaction in a way that makes the detector in efficient to detect any other particle.

Total charge on anode

Now use the primary above and include detector gain to calculate total charge hitting the anode and getting readout.

<References/>

GO BACK [1]