Mechanics in Noninertial Reference Frames
Linearly accelerating reference frames
Let [math]\mathcal S_0[/math] represent an inertial reference frame and \mathcal S represent an noninertial reference frame with acceleration [math]\vec A[/math] relative to [math]\mathcal S_0[/math].
Ball thrown straight up
Consider the motion of a ball thrown straight up as viewed from [math]\mathcal S[/math].
Using a Galilean transformation (not a relativistic Lorentz transformation)
At some instant in time the velocities add like
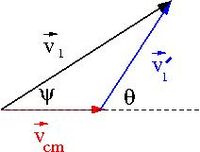
- [math]\dot {\vec {r}_0} = \dot {\vec r}+ \vec V[/math]
where
- [math]\vec V[/math] = velocity of moving frame [math]\mathcal S[/math] with respect to [math]\mathcal S_0[/math] at some instant in time
- [math]\Rightarrow \dot {\vec r} = \dot {\vec {r}_0} - \vec V[/math]
taking derivative with respect to time
- [math]\Rightarrow \ddot {\vec r} = \ddot {\vec {r}_0} - \dot \vec V= \ddot {\vec {r}_0} - \vec A [/math]
- [math]\Rightarrow m\ddot {\vec r} = m\ddot {\vec {r}_0} - m \vec A= \vec F - m\vec A= \vec F - \vec {F}_{\mbox {inertial}}[/math]
where
- [math]\vec {F}_{\mbox {inertial}} = m \vec A \equiv[/math] inertial force
- in your noninertial frame, the ball appears to have a force causing it to accelerate in the [math]\vec A[/math] direction.
The inertial force may also be referred to as a fictional force
an example is the "fictional" centrifugal force for rotational acceleration.
The observer in a noninertial reference frame will feel these frictional forces as if they are real but they are really a consequence of your accelerating reference frame
example
- A force pushes you back into your seat when your Jet airplane takes off
- you slam on the brakes and hit your head on the car's dashboard
Pedulum in an accelerating car
Consider a pendulum mounted inside a car that is accelerating to the right with a constant acceleration [math]\vec A[/math].
What is the pendulums equilibrium angle [math]\theta_0[/math]
In frame [math]\mathcal S_0[/math]
- [math]\sum \vec F = m \ddot{\vec r_0}= \vec T + m \vec g[/math]
In frame [math]\mathcal S[/math]
- [math]\sum \vec F = m \ddot{\vec r}= \vec T + m \vec g - m \vec A= \vec T + m \left ( \vec g -\vec A \right ) = \vec T + m \vec g_{eff} [/math]
If the pendulum is at rest and not oscillating then
- [math]\sum \vec F = 0 = \vec T + m \vec g_{eff} [/math]
[math]g_{eff}[/math] is the vector sum of [math]g[/math] and [math]A[/math] which are orthogonal to each other in this problem thus
- [math]\theta = tan^{-1}{\frac{g}{A}}[/math]
The pendulum oscillation frequency as seen in the accelerating car is
- [math]\omega= \sqrt{\frac{g_{eff}}{l}} = \sqrt{\frac{\sqrt{g^2+A^2}}{l}}[/math]
- Using lagrangian mechanics in the inertial frame
- [math]\vec{r} = (l \sin \theta + \frac{1}{2} a t^2) \hat i + l \cos \theta \hat j[/math]
- [math]\dot \vec{r} = (l \cos \theta \dot \theta + a t) \hat i + \sin \theta \dot \theta \hat j[/math]
- [math] T = \frac{1}{2} mv^2 = \frac{1}{2} m \left ( (l \cos \theta \dot \theta + a t)^2 + \sin^2 \theta \dot \theta^2 \right )[/math]
- [math]= \frac{1}{2} m \left ( l^2 \dot \theta^2 + 2 atl\dot \theta \cos \theta + a^2t^2\right )[/math]
- [math]U =- mgy = -mgl \cos \theta[/math]
- [math]\mathcal L = \frac{1}{2} m \left ( l^2 \dot \theta^2 + 2 atl\dot \theta \cos \theta + a^2t^2\right ) +mgl \cos \theta[/math]
- [math] \left ( \frac{\partial \mathcal {L} }{\partial \theta} \right ) = \frac{d}{dt} \left ( \frac{\partial \mathcal {L} }{\partial \dot \theta} \right ) [/math]
- [math] -matl\sin \theta -mgl\sin \theta = \frac{d}{dt} \left ( ml^2\dot \theta + matl \cos \theta \right ) [/math]
- [math] -at\sin \theta -g\sin \theta = l\ddot \theta - at \sin \theta \dot \theta + a \cos \theta[/math]
- [math] l\ddot \theta=-g\sin \theta + a \cos \theta - at\sin \theta (1+ \dot \theta) [/math]
The tides
The gravitational force between the moon and the earth accelerates the earth and the ocean towards the moon.
The moon of mass [math](M_m)[/math] pulls on the earth of mass [math](M_e)[/math] such that
- [math]\vec F = G \frac{M_m M_e}{d_0^3}\vec d_0 = M_e \vec A[/math]
where [math]d_0[/math] is the earth-moon distance of separation.
- [math]\Rightarrow \vec A = G \frac{M_m }{d_0^3}\vec d_0 =[/math] Earth's acceleration towards the moon that makes the earth a non-inertial reference frame
The moon of mass [math](M_m)[/math] pulls on a test mass of water [math](M_o)[/math] on the surface of the earth's ocean such that
- [math]\vec F = G \frac{M_m M_o}{d^3}\vec d[/math]
As seen in the Earth non-inertial reference frame
- [math]M_o \ddot \vec r = \sum \vec F - M_o \vec A[/math]
- [math]= \left ( M_o \vec g + \vec F_N + G \frac{M_m M_o}{d^3}\vec d \right ) - G \frac{M_m }{d_0^3}\vec d_0 [/math]
where
- [math]\vec F_N =[/math] a net non-graviational force hold the mass M_o in top of the ocean (Bouyant force)
- [math]M_o \ddot \vec r = \left ( M_o \vec g + \vec F_N + G \frac{M_m M_o}{d^3}\vec d \right ) - G \frac{M_m }{d_0^3}\vec d_0 [/math]
- [math]= M_o \vec g + \vec F_N + \vec{F}_{\mbox{tide}}[/math]
- [math]\vec{F}_{\mbox{tide}} = G \frac{M_m M_o}{d^3}\vec d - G \frac{M_m }{d_0^3}\vec d_0 [/math]
- [math] = G M_m M_o \left ( \frac{\vec d}{d^3} - \frac{\vec d_0}{d_0^3}\right ) [/math]
Let's consider two cases, one where M_o is directly between the moon and the earth and the other when the mass is directly on the opposite side of the earth from the moon.
- Case 1
- The mass is directly between the moon and the earth
- In this case [math]\vec d || \vec d_0 [/math] and [math]d_0 \lt d[/math] making [math]\vec{F}_{\mbox{tide}}[/math] pull [math]M_o[/math] towards the moon
- Case 2
- The mass is directly on the other side of the earth with respect to the moon
- In this case [math]\vec d || \vec d_0 [/math] BUT [math]d_0 \gt d[/math] making [math]\vec{F}_{\mbox{tide}}[/math] pull [math]M_o[/math] away from the moon
Forest_Ugrad_ClassicalMechanics
