Forest PHYS100 Demos Week5
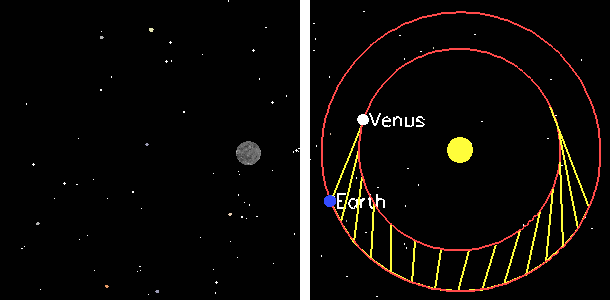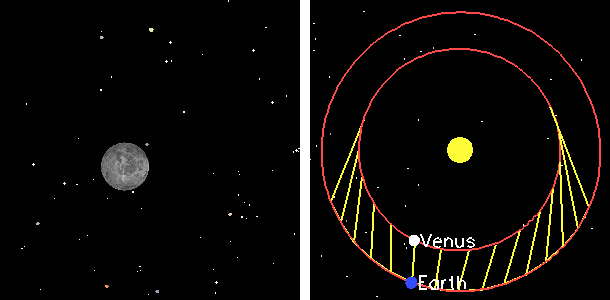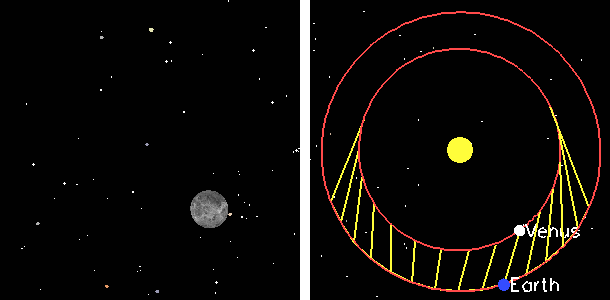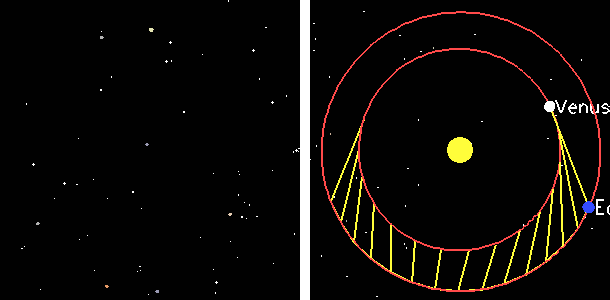
Retrograde motion animated gif
Cut the Rope
For this demonstration I will ask the students what the central force keeping the ball moving in a circle would be. The correct answer is the tension on the string. After this I will swing the ball around and ask the students what the approximate trajectory of the ball will be if we sever the rope connecting the ball when the string and the ball are perpendicular to the force of gravity. The correct answer is that the ball will fly off tangentially, which in this case would be straight up in the air.
Glass Platform Spin:
For this demonstration I will start with an anecdote about a swing set. No matter how hard you try by yourself, you are unable to make the swing fully rotate over the top bar with you on the swing. Why is this? The correct answer is that you don’t have enough of a centripetal acceleration in order to keep the chains tight on the swing, so they go slack. This will mean that the earth’s gravity will take over and you will fall on the top bar. What if you could swing fast enough? What would the motion of the swing look like? You are able to maintain uniform circular motion because the centripetal acceleration towards the center of the circle is greater than the acceleration due to gravity. I will then ask them what would will happen if I swing the platform over my head? The answer is that the wine glass will stay on the platform due to a higher centripetal acceleration than gravity.
Roulette Wheel:
For this demonstration I will ask the students what the minimum angular velocity will be in order to keep the ball in the wheel without falling. The answer is that minimally we will at least need the force of gravity to be equall to the normal force. We can set the normal force equal to mv^2/r where m is the mass of the ball and r is the radius of the loop. We can solve for v and find the angular velocity by dividing v by r. Alternatively you can set mg = m(omega)^2*r and solve for omega.