Forest UCM NLM AtwoodMachine

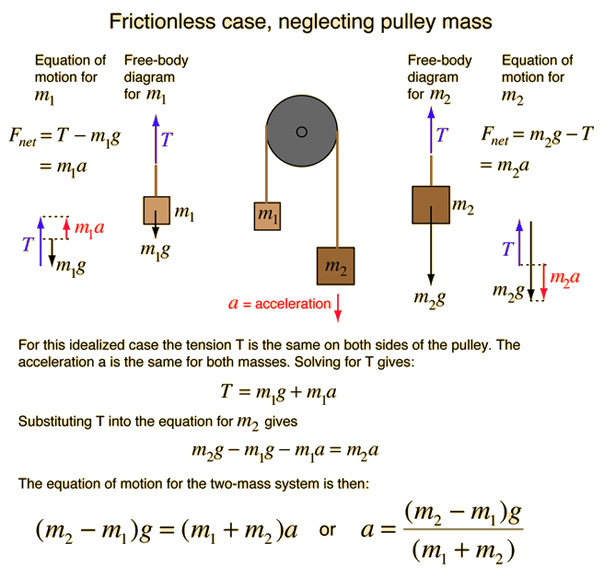
Simple Atwood's machine

[math]\Rightarrow T = \frac{2m_1m_2}{m_1+m_2} g[/math]

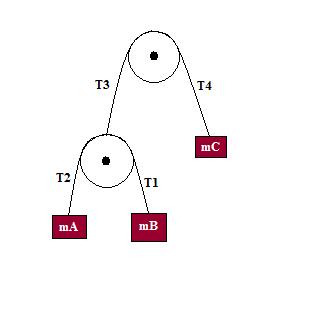
Double Atwood's machine

The problem

Determine the acceleration of each mass in the above picture.

Step 1: Identify the system

Each block is a separate system with two external forces; a gravitational force and the rope tension.

Step 2: Choose a suitable coordinate system

A coordinate system with one axis that defines the posive direction as up is one possible orientation.

Step 3: Draw the Free Body Diagram

200 px

Step 4: Define the Force vectors using the above coordinate system

for mass 1

[math]T_1 - m_1 g = m_1 a_1[/math]

for mass 2

[math]T_2 - m_2 g = m_2 a_2[/math]

for mass 3

[math]T_3 - m_3 g = m_3 a_3[/math]

If we know the mass of all the objects in the system then we are left with three unkown Tensions and three unknown acceleratios. In total we currently have 6 unkowns and 3 equations.

Using Newton's first law we know that T_1 = T_2

We need three more equations!

External Forces on Lower pulley

Consider the external forces acting on the MASSLESS lower pulley

T_3-T1-T2 = (0)a

Step 5: Use Newton's second law

Forest_UCM_NLM#Atwoods_Machine