Forest UCM NLM GalileanTans
File:TF UCM GalileanTans RefFrame.xfig.txt
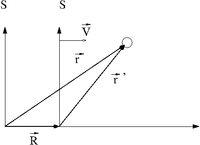
Assume that is a coordinate system moving at a CONSTANT speed with respect to a fixed coordinate system .
Let and describe the position an object in motion using two different coordinate systems and respectively.
represents a vector that locates the origin of the moving reference frame () with respect to the origin of reference from .
Using the definition of vector addition
Similarly
and
Newton's law of motion may be written as
If
- is moving at a constant velocity
Then
Newton's law hold in coordinate system which move at a constant velocity (an inertial reference frame). Accelerating reference frames are know as non-inertial reference frames and will be discussed later. (a coordinate system fixed to the Earth is a non-inertial reference frame since the Earth is rotating about its axis and moving in orbit about the Sun)
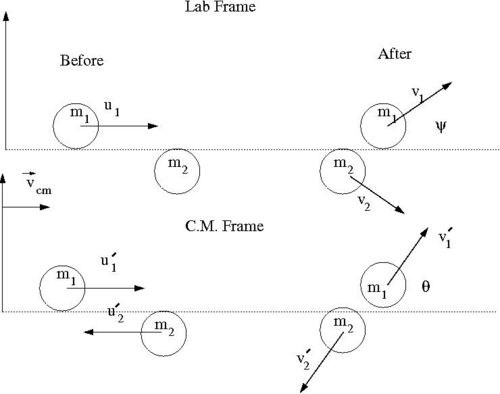
Galiean Transformation to CM frame
Consider the elastic scattering of two hard spheres from a fixed reference frame (Lab Frame) and an inertial frame moving at a speed such that the velocities of the two spheres are equal in magnitude but opposite in direction.