Relative efficiency
Some papers
File:Nn correlation extraction.pdf
Rletive efficiency obtained from the 2n opening angle w/ uncorrelated neutrons
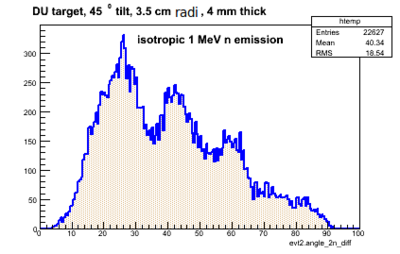
The result of simulation of 2n openeing angle obtained by different neutron detectors (each neutron hit different detector) having y-resolution is presented below. The source of neutrons was isotropic.
| Empty target, events sampled | DU target, events sampled |
|---|---|
|
|
| Point isotropic n-source w/o material | Volume isotropic n-source + DU material |
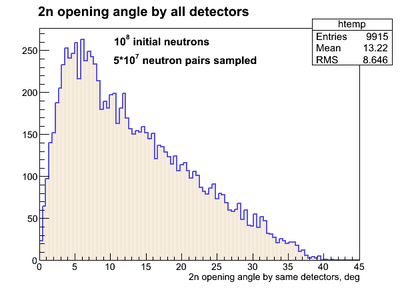
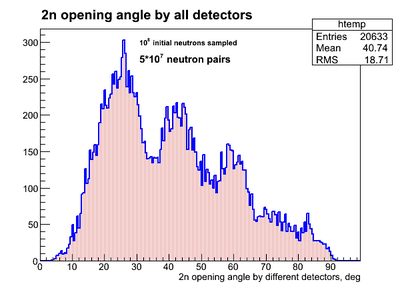
The result of simulation of 2n openeing angle obtained by the same neutron detectors (2 neutrons hit same detector) having y-resolution is presented below:
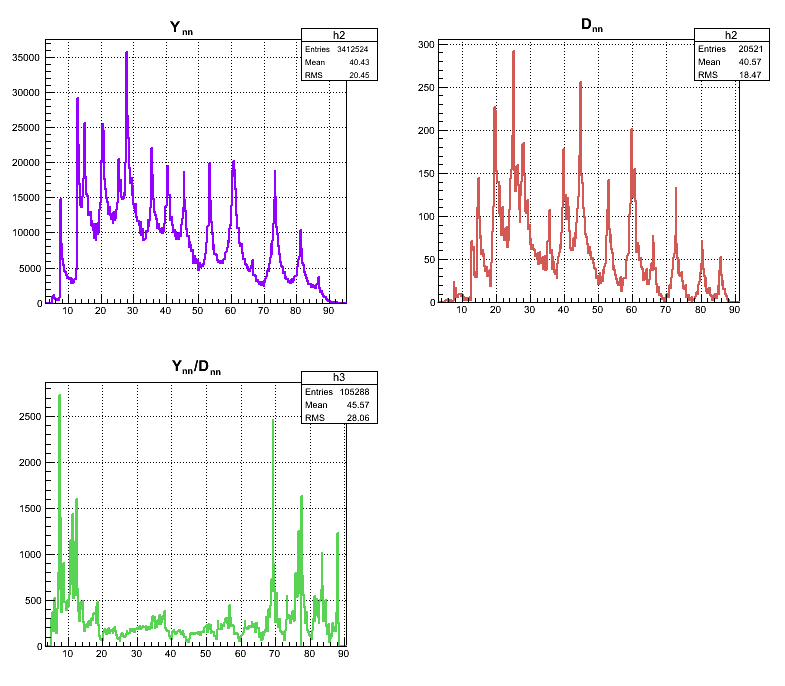
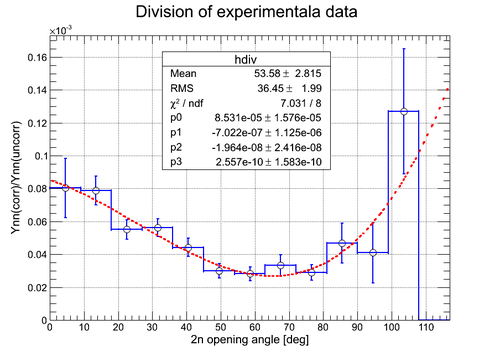
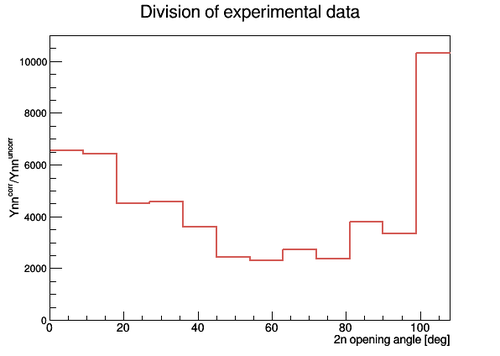
In the experiment our expereimental setup did not have y-resolution across the surface of the neutron detectors. So it was necessary to simulate the 2n opening angle for the neutron detectors w/o y-resolution. The result of the simulation of 2n opening angle (the 2n angles detected by all detectors are superimposed) for the case where thre was no y-resolution is going to be noted as . The experimental data obtained from run 4172 (DU target) on 2n opening angle for uncorrelated neutrons (i.e. in the case of isotropic source of neutrons) from different pulses is going to be noted as . The relative efficiency is defined as and it is plotted below as a result of bib-by-bin division of over .
Relative efficiency of the detecting system obtained using experimental data only (all runs)
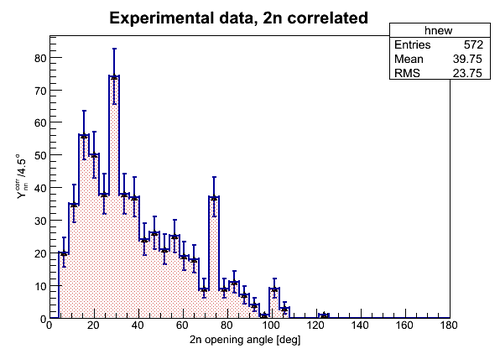
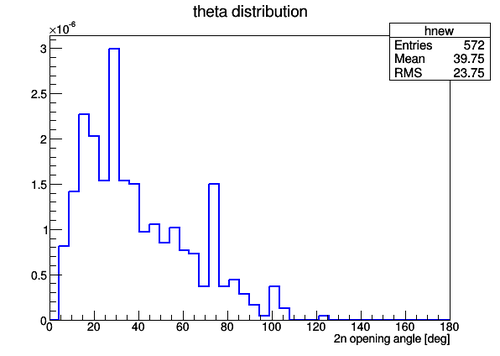
In this part the experimantal data are presented for the cases when (1) the 2n opening angle was measured for neutrons correlated and (2) the 2n opening angle was measured for neutrons uncorrelated (neutrons from separate pulses). In the figure below the experimental data on the 2n opening angle measured for the case of correlated neutrons is presented where the statistical error bar width is equal to along y-axis and 4.5 deg along x-axis (the bin width). The total number of triggering pulses during the experiment was Nexp_pulses=2.469256E+7.
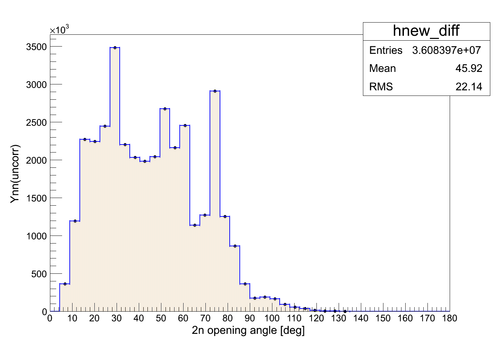
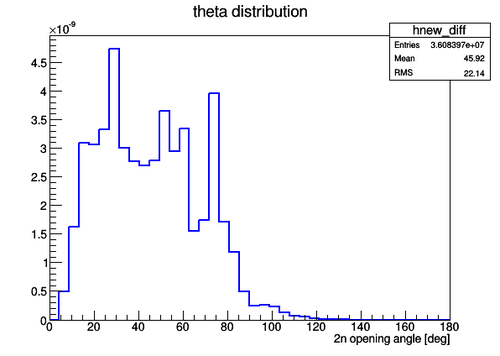
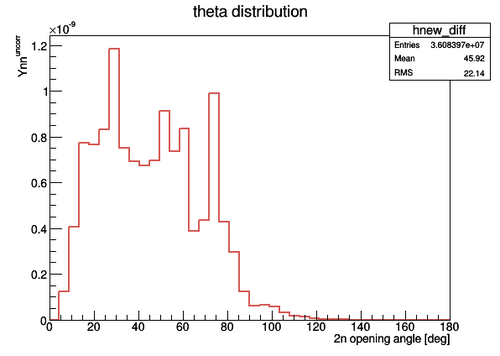
The experimental data on the 2n opening angle measured for the case of uncorrelated neutrons is presented in the next figure. 80 neutrons from different pulses were taken uniformly to reproduce 2n opening angle for the case of uncorrelated neutrons. The total number of uncorrelated neutron pairs was Npair_uncorr = 3.608397E+7. The width of the error bars is smaller then the size of the markers.
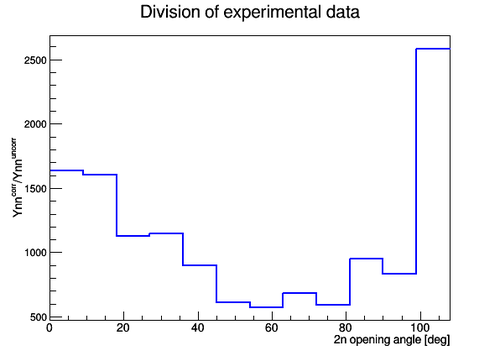
The result of the division of the two histograms () obtained for the described two cases is shown below. In order to obtain the resulting histogram as a division of the previous two histograms we need to do the division on the bin-by-bin basis as , where and are the contents of the corresponding bins and and are the coresponding statistical errors for the bin contents and . The error bars were obtained by the propagation in the following way: . The resulting histogram wa normalized to the ratio of the total number of pulses to the total number of uncorrelated neutron pairs considered Norm = Nexp_pulses/Npair_uncorr = 2.469256E+7/3.608397E+7 . It should be noted that the total number of uncorrelated neutron pairs can be varied by changing the number of corresponding combinations and the number of pulses involved into the 2n opening angle reproduction, so the normalization may change.
Normalization
Data table 1.
| run# | Total # of pulses per run |
|---|---|
| run4118 | 1668482 |
| run4119 | 2135901 |
| run4133 | 1704331 |
| run4134 | 1732490 |
| run4135 | 1603604 |
| run4137 | 800699 |
| run4144 | 1645667 |
| run4145 | 1544605 |
| run4146 | 510826 |
| run4153 | 1750657 |
| run4154 | 1631436 |
| run4155 | 1062048 |
| run4166 | 214600 |
| run4169 | 191592 |
| run4170 | 429974 |
| run4171 | 1141113 |
| run4172 | 650734 |
| run4173 | 354992 |
| run4174 | 953831 |
| run4175 | 299086 |
| run4176 | 144774 |
| run4177 | 225877 |
| run4203 | 659050 |
| run4204 | 1636192 |
| totals | 24692561 |
Normalization factor is 24692561.
Data table 2. Uncorrelated neutron pairs.
| run# | 80 puls pairs | all nonZ pairs | total # of pairs |
|---|---|---|---|
| run4118 | 1949796 | 35168980 | 58460510939894 |
| run4119 | 2470399 | 57115623 | 95803579611944 |
| run4133 | 1741760 | 30145143 | 60999663129029 |
| run4134 | 1832885 | 33384324 | 63031990015343 |
| run4135 | 1727993 | 28580648 | 54002495269034 |
| run4137 | 833189 | 7099684 | 13463513489481 |
| run4144 | 1770693 | 26603021 | 56872651957830 |
| run4145 | 1592222 | 20562899 | 50101929186175 |
| run4146 | 491705 | 2157292 | 5479817982802 |
| run4153 | 8753312 | 177560268 | 64360835399566 |
| run4154 | 1695297 | 26345381 | 55893286150871 |
| run4155 | 1182325 | 12257834 | 23686887361551 |
| run4166 | 174390 | 226636 | 967120869210 |
| run4169 | 175558 | 235498 | 770861409690 |
| run4170 | 319678 | 1008712 | 3882439488990 |
| run4171 | 1415700 | 19159461 | 27344940440490 |
| run4172 | 623978 | 3412116 | 8892563188751 |
| run4173 | 395573 | 1327163 | 2646413182232 |
| run4174 | 894440 | 5765727 | 19105685150123 |
| run4175 | 255450 | 619705 | 1878507428108 |
| run4176 | 110058 | 119818 | 440152774689 |
| run4177 | 976415 | 1721476 | 1071433552715 |
| run4203 | 3003073 | 23564022 | 9121298818219 |
| run4204 | 1682843 | 28829022 | 56219643867161 |
| totals | 36068732 | 542970453 | 734498220663898 |
The normalization factor is 734498220663898.
And the division of the normalized plots gives the following 2n opening angle distribution
If the normalization factor is four times larger 4*734498220663898 then the normalized 2n opening angle distribution in the case of uncorrelated neutron pairs looks like
And the division of the normalized plots gives the following 2n opening angle distribution