Alpha Ionization

Energy threshold for electron and gamma entering detector

Detemine the energy threshold that an electron and a photon need to surpass in order to pass through the kapton, gas, the copper cathode, and the FR4.

Draw a picture with dimensions of all the layers

Energy -vs- counts per incident particle

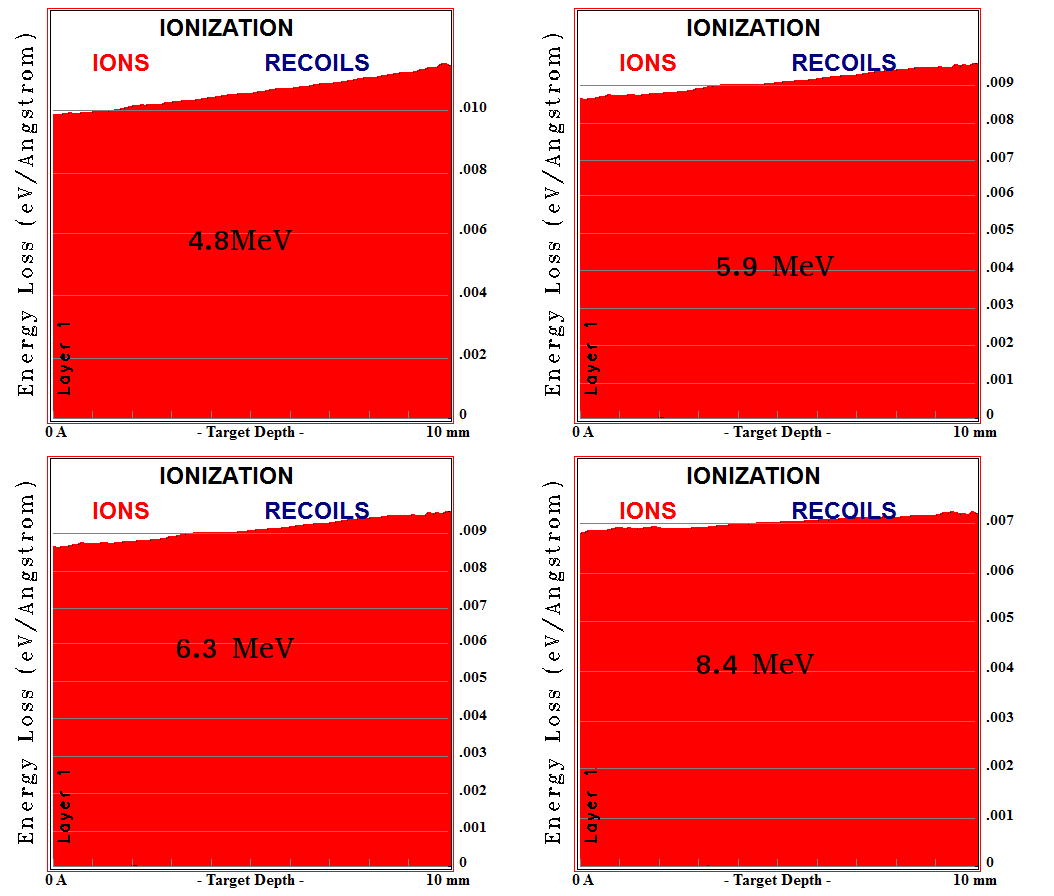
Alpha Particles ionization simulation using GEANT4

GEANT4 simulates the ionization of alpha particles in Ar/CO2 90/10 gas. Geant4 can simulate the ionization process for alpha particles. Unfortunately the value of the step function underestimates the number of delta electrons even after decreasing the step cut to 1 nm. Also,using GEANT4 overestimates the range of alpha particles in Ar/CO2 gas when compared to those that srim calculates File:Alpha range ArCo2.txt, the following table shows the maximum range of alpha particles that are emitted from the U-233, and the ranges calculated by srim.

Alpha Energy (MeV)	G4 Range (cm)	Srim Range (um)
1.0	0.56599	129.49
2.0	1.1467	255.91
3.0	1.9024	417.27
4.0	2.8012	612.45
5.0	3.8425	839.91

Based on the previous table, GEANT4 failed to calculate the expected alpha range for most alpha energies, and underestimated the number of alpha's delta electrons emitted through that range, but it is still useful tool to simulate the primary delta electrons when negative beta particles pass through a defined medium.

Calculating the number of the delta electrons without using GEANT4

There is another way to calculate the number of delta electrons without using GEANT4. It starts by calculating the average energy loss [math] \Delta E_a[/math] by the alpha particles and the average energy loss per unit length [math] {\zeta} [/math] in Ar/CO2 gas using the Bethe-Block equation. It then uses the the following equation:

[math] \lambda = \frac{ \Delta E - \Delta E_a}{\zeta} [/math]

to calculate the actual energy loss by ionization [math] \Delta E [/math], where [math] \lambda [/math] represents random landau number.

By dividing the energy loss by the minimum energy for producing a pair of ion/electron pair W, this equation yields the number of electrons emitted by ionization.

Srim can simulate the motion of an alpha particle in Ar/CO2 gas by allowing for the change in the stopping power per unit length. It can also show the ionization energy loss as shown in the following figure:

This figure shows the ionization energy loss of 999 alpha particles as they pass through Ar/CO2 gas. Integrating the area under the curve and dividing by (W*1000) will estimate the number of delta electrons produced by an alpha particle.

Bethe block formula calculates the average ionization energy loss as the following: [math]- \frac{dE}{dx} = \frac{4 \pi}{m_e c^2} \cdot \frac{nz^2}{\beta^2} \cdot \left(\frac{e^2}{4\pi\varepsilon_0}\right)^2 \cdot \left[\ln \left(\frac{2m_e c^2 \beta^2}{I \cdot (1-\beta^2)}\right) - \beta^2\right][/math]

for an electron of rest mass [math] mc^2 = 0.511 MeV [/math],

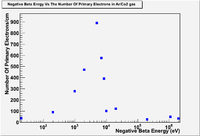
Number of Primary ionization events per cm

from beta particle as a function of beta particle energy using Garfield and GEANT4

GEANT4 can simulate the primary number of delta electrons for a negative beta particle penetrating ArCO2. Using TestEm10 example and choosing appropriate default cut, GEANT4 counts the same number of primary delta electrons for a 1.1 MeV negative beta particles, and determines the energy of the delta electrons energy and momentum depending on Moller or Bhabha's scattering depending on the value of the kinetic energy cut used.<ref name = "Urban">Urbán, L. (1998, 10 09). Geant4 physics reference manual. Retrieved from http: //geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/node41.html </ref>

The following figure shows the number of the primary electrons that are emitted from negative beta with energy E, passing through a 90/10 Ar/CO2 gas:

Overlay with dE/dx formula and fill in gaps

something is wrong with G4 result for electron energies below 1 keV.

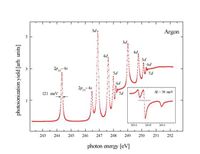
from photon as a function of photon particle energy using Garfield and GEANT4

Detector Geometry in GEANT4

The physical interactions that take place inside the detector is simulated by GEANT4.9.6 to estimation the primary charge collected by the drift electric in GEM detector. GEM detector depends mainly on the particles interaction with Ar/CO2 atoms and molecules, especially the ones that directly (or indirectly) produce free charge that can be collected by the drift electric field. Specifically for the GEM detector described in section XX, the detector signal can be produced by gamma, electrons or neutrons. GEANT4.9.6 has been used to estimate the primary charge caused by those particles,

<References/>