Kiwi Dipole Mappings
Kiwi Dipole Documents
Cad drawing of kiwi dipole:
File:Hrrl pos wiki dipole 1.pdf File:Hrrl pos wiki dipole 2.pdf File:Hrrl pos wiki dipole 3.pdf File:Hrrl pos wiki dipole 4.pdf File:Hrrl pos wiki dipole 5.pdf
Bending Radius of the kiwi dipole is 318.5 mm, and it bends beam by 45 degree.
The path of the beam in the dipole then
1st Mapping
File:Kiwi Dipole Magnet Mappings.pdf
Tag Number: 079220
Bending magnet that was to be used with LCS (compact magnets) The horizontal and vertical tranlator have a range for 150 mm i.e. 15 cm.
Power on I = 20.4 A
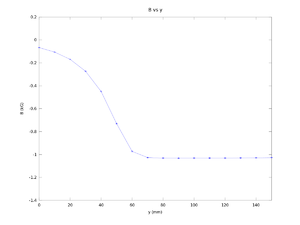
| x (mm) | y (mm) | B (kG) | |
| 127 | 0 | ||
| 127 | 10 | -0.106 | |
| 127 | 20 | -0.169 | |
| 127 | 30 | -0.2729 | |
| 127 | 40 | -0.448 | |
| 127 | 50 | -0.728 | |
| 127 | 60 | -0.97 | |
| 127 | 70 | -1.025 | |
| 127 | 80 | -1.029 | |
| 127 | 90 | -1.03 | |
| 127 | 100 | -1.029 | |
| 127 | 110 | -1.028 | |
| 127 | 120 | -1.028 | |
| 127 | 130 | -1.028 | |
| 127 | 140 | -1.028 | |
| 127 | 150 | -1.028 | |
| y = 150 mm is roughly center of the bend. | |||
| 127 | 150 | -1.028 | |
| 127 | 140 | -1.031 | |
| 127 | 130 | -1.0342 | |
| 127 | 120 | -1.036 | |
| 127 | 110 | -1.036 | |
| 127 | 100 | -1.036 | |
| 127 | 90 | -1.036 | |
| 127 | 80 | -1.0355 | |
| 127 | 70 | -1.03 | |
| 127 | 60 | -0.977 | |
| 127 | 50 | -0.7354 | |
| 127 | 40 | -0.4527 | |
| 127 | 30 | -0.275 | |
| 127 | 20 | -0.17 | |
| 127 | 10 | -0.1066 | |
| 127 | 0 | -0.0673 | |
| Again | |||
| x (mm) | y (mm) | B (kG) | |
| 127 | 0 | ||
| 127 | 10 | -0.1062 | |
| 127 | 20 | -0.1699 | |
| 127 | 30 | -0.2738 | |
| 127 | 40 | -0.449 | |
| 127 | 50 | -0.7283 | edge of poles 100 px |
| 127 | 60 | -0.9712 | |
| 127 | 70 | -1.0253 | |
| 127 | 80 | -1.03 | |
| 127 | 90 | -1.03 | |
| 127 | 100 | -1.0298 | |
| 127 | 110 | -1.028 | |
| 127 | 120 | -1.0285 | |
| 127 | 130 | -1.0286 | |
| 127 | 140 | -1.0282 | |
| 127 | 150 | -1.0278 |
y (mm) B (kG) error B (kG)
0.00000 -0.06717 0.00015
10.00000 -0.10627 0.00031
20.00000 -0.16963 0.00055
30.00000 -0.27390 0.00105
40.00000 -0.44990 0.00248
50.00000 -0.73057 0.00419
60.00000 -0.97273 0.00374
70.00000 -1.02677 0.00280
80.00000 -1.03150 0.00350
90.00000 -1.03200 0.00346
100.00000 -1.03160 0.00383
110.00000 -1.03067 0.00462
120.00000 -1.03083 0.00448
130.00000 -1.03027 0.00342
140.00000 -1.02907 0.00168
150.00000 -1.02793 0.00012
X at 127, Y at 150
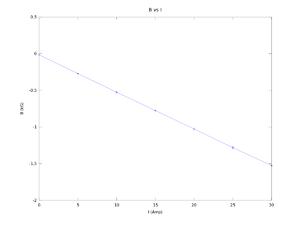
| x (mm) | y (mm) | I | B (kG) | |
| 127 | 150 | 20.1 | -1.0279 | |
| 127 | 150 | 30.1 | -1.53 | |
| 127 | 150 | 25.1 | -1.2916 | |
| 127 | 150 | 20.1 | -1.0359 | |
| 127 | 150 | 15 | -0.781 | |
| 127 | 150 | 10 | -0.534 | |
| 127 | 150 | 5 | -0.277 | |
| 127 | 150 | 0 | -0.017 | |
| Again | ||||
| 127 | 150 | 0 | -0.01726 | |
| 127 | 150 | 5 | -0.266 | |
| 127 | 150 | 10 | -0.518 | |
| 127 | 150 | 15 | -0.7713 | |
| 127 | 150 | 20 | -1.02 | |
| 127 | 150 | 25 | -1.272 | |
| 127 | 150 | 30 | -1.52 |
I (Amps) B (kG) error B (kG) 0.00000 -0.01713 0.00018 5.00000 -0.27150 0.00778 10.00000 -0.52600 0.01131 15.00000 -0.77615 0.00686 20.00000 -1.02795 0.01124 25.00000 -1.28180 0.01386 30.00000 -1.52500 0.00707
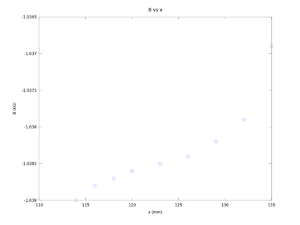
Vertical Scan
Power on I = 20 A
Gap width 5cm.
| x (mm) | y (mm) | B (kG) | |
| 135 (lower edge) | 150 | -1.0369 | |
| 132 | 150 | -1.0379 | |
| 129 | 150 | -1.0382 | |
| 126 | 150 | -1.0384 | |
| 123 | 150 | -1.0385 | |
| 120 | 150 | -1.0386 | |
| 118 | 150 | -1.0387 | |
| 116 | 150 | -1.0388 | |
| 114 | 150 | -1.039 |
x (mm) y(mm) B(kG) 135.0000 150.0000 -1.0369 132.0000 150.0000 -1.0379 129.0000 150.0000 -1.0382 126.0000 150.0000 -1.0384 123.0000 150.0000 -1.0385 120.0000 150.0000 -1.0386 118.0000 150.0000 -1.0387 116.0000 150.0000 -1.0388 114.0000 150.0000 -1.0390
Horizontal Scan
go for X = 124.5, y = 150 (dipole center), I = 20 A.
| x (mm) | y (mm) | I (A) | B (kG) | |
| 124.5 | 150 | 20 | -1.0388 | |
| 124.5 | 140 | 20 | -1.04 | |
| 124.5 | 130 | 20 | -1.04 | |
| 124.5 | 120 | 20 | -1.0409 | |
| 124.5 | 110 | 20 | -1.041 | |
| 124.5 | 100 | 20 | -1.0411 | |
| 124.5 | 90 | 20 | -1.041 | |
| 124.5 | 80 | 20 | -1.0408 | |
| 124.5 | 70 | 20 | -1.355 | This data is problematic. |
| 124.5 | 60 | 20 | -0.9799 | |
| 124.5 | 50 | 20 | -0.74 | |
| 124.5 | 40 | 20 | -0.457 | |
| 124.5 | 30 | 20 | -0.2776 | |
| 124.5 | 20 | 20 | -0.1718 | |
| 124.5 | 0 | 20 | -0.0684 |
Figure according to the data above. There is problem when y = 70 mm.
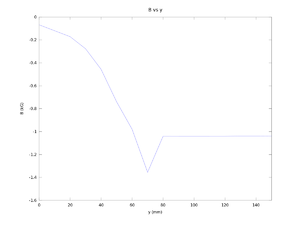
x (mm) y (mm) I (A) B (kG) 124.50000 150.00000 20.00000 -1.03880 124.50000 140.00000 20.00000 -1.04000 124.50000 130.00000 20.00000 -1.04000 124.50000 120.00000 20.00000 -1.04090 124.50000 110.00000 20.00000 -1.04100 124.50000 100.00000 20.00000 -1.04110 124.50000 90.00000 20.00000 -1.04100 124.50000 80.00000 20.00000 -1.04080 124.50000 70.00000 20.00000 -1.03550 124.50000 60.00000 20.00000 -0.97990 124.50000 50.00000 20.00000 -0.74000 124.50000 40.00000 20.00000 -0.45700 124.50000 30.00000 20.00000 -0.27760 124.50000 20.00000 20.00000 -0.17180 124.50000 0.00000 20.00000 -0.06840
Figure according to the data above. The problem when y = 70 mm is changed to -1.0355
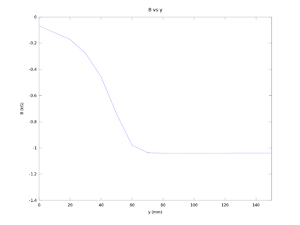
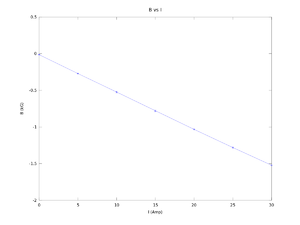
Power on X = 124.5, Y = 150
| x (mm) | y (mm) | I (A) | B (kG) | |
| 124.5 | 150 | 0 | -0.0123 | |
| 124.5 | 150 | 5 | -0.2676 | |
| 124.5 | 150 | 10 | -0.516 | |
| 124.5 | 150 | 15 | -0.771 | |
| 124.5 | 150 | 20 | -1.028 | |
| 124.5 | 150 | 25 | -1.2735 | |
| 124.5 | 150 | 30 | -1.5217 | |
| 124.5 | 150 | 30 | -1.5218 | |
| 124.5 | 150 | 25 | -1.287 | |
| 124.5 | 150 | 20 | -1.037 | |
| 124.5 | 150 | 15 | -0.7855 | |
| 124.5 | 150 | 10 | -0.5313 | |
| 124.5 | 150 | 5 | -0.2747 | |
| 124.5 | 150 | 0 | -0.0164 |
I (A) B(kG) error B(kG) 30.00000 -1.52175 0.00007 25.00000 -1.28025 0.00955 20.00000 -1.03250 0.00636 15.00000 -0.77825 0.01025 10.00000 -0.52365 0.01082 5.00000 -0.27115 0.00502 0.00000 -0.01435 0.00290
Tag Number: 42125
| x (mm) | y (mm) | I (A) | B (kG) | |
| 0 | 0 | Power off | ||
| 0 | 0 | 20 | ||
| 111.75 | 0 | 20 |
| x (mm) | y (mm) | I (A) | B (kG) |
| 111.75 | 10 | 20 | 0.0637 |
| 111.75 | 20 | 20 | 0.102 |
| 111.75 | 30 | 20 | 0.1675 |
| 111.75 | 40 | 20 | 0.2774 |
| 111.75 | 50 | 20 | 0.4654 |
| 111.75 | 60 | 20 | 0.756 |
| 111.75 | 70 | 20 | 0.9898 |
| 111.75 | 80 | 20 | 1.0312 |
| 111.75 | 90 | 20 | 1.0358 |
| 111.75 | 100 | 20 | 1.0362 |
| 111.75 | 110 | 20 | 1.0363 |
| 111.75 | 120 | 20 | 1.0363 |
| 111.75 | 130 | 20 | 1.0362 |
| 111.75 | 140 | 20 | 1.036 |
| 111.75 | 150 | 20 | 1.036 |
| 111.75 | 0 | 20 | 0.0402 |
| 111.75 | 10 | 20 | 0.0635 |
| 111.75 | 20 | 20 | 0.1022 |
| 111.75 | 30 | 20 | 0.1674 |
| 111.75 | 40 | 20 | 0.2773 |
| 111.75 | 50 | 20 | 0.4652 |
| 111.75 | 60 | 20 | 0.755 |
| 111.75 | 70 | 20 | 0.9828 |
| 111.75 | 80 | 20 | 1.0312 |
| 111.75 | 90 | 20 | 1.0358 |
| 111.75 | 100 | 20 | 1.0362 |
| 111.75 | 110 | 20 | 1.0362 |
| 111.75 | 120 | 20 | 1.03625 |
| 111.75 | 130 | 20 | 1.0362 |
| 111.75 | 140 | 20 | 1.036 |
| 111.75 | 150 | 20 | 1.036 |
| x (mm) | y (mm) | I (A) | B (kG) |
| 111.75 | 150 | 0 | 0.0076 |
| 111.75 | 150 | 5 | 0.263 |
| 111.75 | 150 | 10 | 0.52 |
| 111.75 | 150 | 15 | 0.7754 |
| 111.75 | 150 | 20 | 1.0313 |
| 111.75 | 150 | 25 | 1.2869 |
| 111.75 | 150 | 30 | 1.5389 |
| 111.75 | 150 | 30 | 1.5389 |
| 111.75 | 150 | 25 | 1.3 |
| 111.75 | 150 | 20 | 1.0484 |
| 111.75 | 150 | 15 | 0.7945 |
| 111.75 | 150 | 10 | 0.534 |
| 111.75 | 150 | 5 | 0.276 |
| 111.75 | 150 | 0 | 0.01386 |
| x (mm) | y (mm) | I (A) | B (kG) |
| 123.25 | 150 | 20 | 1.0339 |
| 120.25.25 | 150 | 20 | 1.0338 |
| 117.25 | 150 | 20 | 1.034 |
| 114.25 | 150 | 20 | 1.034 |
| 111.25 | 150 | 20 | 1.0342 |
| 111.25 | 150 | 20 | 1.0343 |
| 108.25 | 150 | 20 | 1.0342 |
| 105.25 | 150 | 20 | 1.0343 |
| 102.25 | 150 | 20 | 1.0344 |
| 99.25 | 150 | 20 | 1.03435 |
| x (mm) | y (mm) | I (A) | B (kG) |
| 111.25 | 150 | 20 | 1.0339 |
| 111.25 | 0 | 20 | 0.04 |
| 111.25 | 10 | 20 | 0.0633 |
| 111.25 | 20 | 20 | 0.102 |
| 111.25 | 30 | 20 | 0.1671 |
| 111.25 | 40 | 20 | 0.2767 |
| 111.25 | 50 | 20 | 0.4643 |
| 111.25 | 60 | 20 | 0.7544 |
| 111.25 | 70 | 20 | 0.9818 |
| 111.25 | 80 | 20 | 1.0295 |
| 111.25 | 90 | 20 | 1.034 |
| 111.25 | 100 | 20 | 1.0344 |
| 111.25 | 110 | 20 | 1.0345 |
| 111.25 | 120 | 20 | 1.0345 |
| 111.25 | 130 | 20 | 1.0345 |
| 111.25 | 140 | 20 | 4.0343 |
| 111.25 | 150 | 20 | 10.342 |
| 111.25 | 0 | 20 | 0.04 |
| 111.25 | 10 | 20 | 0.0632 |
| 111.25 | 20 | 20 | 0.1018 |
| 111.25 | 30 | 20 | 0.1669 |
| 111.25 | 40 | 20 | 0.2767 |
| 111.25 | 50 | 20 | 0.4639 |
| 111.25 | 60 | 20 | 0.754 |
| 111.25 | 70 | 20 | 0.9816 |
| 111.25 | 80 | 20 | 1.0294 |
| 111.25 | 90 | 20 | 1.034 |
| 111.25 | 100 | 20 | 1.0344 |
| 111.25 | 110 | 20 | 1.0344 |
| 111.25 | 120 | 20 | 1.0344 |
| 111.25 | 130 | 20 | 1.0343 |
| 111.25 | 140 | 20 | 4.0342 |
| 111.25 | 150 | 20 | 10.342 |
| x (mm) | y (mm) | I (A) | B (kG) |
| 111.25 | 43 mm | 0 | |
| 111.25 | 43 mm | 5 | 0.0822 |
| 111.25 | 43 mm | 10 | 0.1615 |
| 111.25 | 43 mm | 15 | 0.242 |
| 111.25 | 43 mm | 20 | 0.3227 |
| 111.25 | 43 mm | 25 | 0.4014 |
| 111.25 | 43 mm | 30 | 0.4793 |
| 111.25 | 43 mm | 0 | |
| 111.25 | 43 mm | 5 | 0.08 |
| 111.25 | 43 mm | 10 | 0.1613 |
| 111.25 | 43 mm | 15 | 0.242 |
| 111.25 | 43 mm | 20 | 0.3215 |
| 111.25 | 43 mm | 25 | 0.4 |
| 111.25 | 43 mm | 30 | 0.4783 |
2nd Mapping
Bending radius of dipole is 319 mm. The bending radius in measurement is r = 280 mm.
Mapping of the dipole was divided into 3 parts according to the path of the ideal particle. This trajectory of particle with ideal energy should go through a fringe field (approximately straight line) and dipole field (rotation of near 45 degree with dipole bending radius of 319 mm), and another fringe field (approximately straight line). We called them A2 (entering fringe field), Rotation and A1 (Exiting fringe field).
A2
I= - 6.5 A I= - 15.25 A I= - 24 A I= - 33 A Z(mm) B (G) B (G) B (G) B (G) 81.50 -55.2500 -128.3700 200.6800 -273.6085 82.50 -52.6000 -122.1600 -191.0000 -260.3194 83.50 -50.0700 -116.2700 -181.7600 -247.6903 84.50 -47.6700 -110.6800 -173.0100 -235.7135 85.50 -45.4000 -105.3700 -164.6920 87.50 -41.1800 -95.5400 -149.2710 -203.2767 89.50 -37.3800 -86.6600 -135.3760 -184.2830 91.50 -33.9600 -78.6600 -122.8530 -167.1615 93.50 -30.8600 -71.4600 -111.5640 -151.7285 95.50 -28.0800 -64.9700 -101.3870 -137.8432 98.00 -25.1200 -57.7600 -90.1060 -122.3860 100.00 -22.8900 -52.6200 -82.0500 -111.3860 103.00 -19.9800 -45.8400 -71.4230 -96.9286 105.00 -18.2600 -41.8600 -65.1930 -88.3740 110.00 -14.6600 -33.5200 -52.1380 -70.5650 115.00 -11.8500 -27.1700 -41.9210 120.00 -9.6500 -22.0600 -34.0260 -45.8887 130.00 -6.5400 -14.8400 -22.9290 -30.7577 140.00 -4.5600 -10.2500 -15.7670 -21.0309 150.00 -3.2600 -7.2600 -11.0980 -14.7070
A1
I= - 6.505 A I= - 15.25 A I= - 24 A I= - 33 A Z(mm) B (G) B (G) Z(mm) B (G) B (G) 137.50 -69.4460 -160.7070 137.50 -252.3900 -342.9800 136.50 -66.4320 -153.7000 136.50 -241.2700 -328.0530 135.50 -63.5170 -146.9330 135.50 -230.6500 -313.6100 134.50 -60.7320 -140.4650 134.50 -220.5150 -299.7060 133.50 -58.0720 -134.2840 133.50 -210.8160 -286.0330 132.50 -128.3450 133.00 -206.0800 -279.6640 132.00 -54.3030 -125.5330 132.00 -197.0500 -267.3660 131.00 -51.9270 -120.0150 131.00 -188.4130 -255.5850 130.00 -49.6620 -114.7500 130.00 -180.1390 -244.2880 128.00 -45.4210 -104.9110 128.00 -164.6400 -223.1900 126.00 -41.5550 -95.9450 126.00 -150.5300 -204.0060 124.00 -38.0300 -87.7600 124.00 -137.6900 -186.4830 122.00 -34.8100 -80.2900 122.00 -125.9700 -170.5440 120.00 -31.8780 -73.4860 120.00 -115.2900 -156.0020 118.00 -29.2060 -67.2900 118.00 -105.5500 -142.7470 116.00 -26.7690 -61.6400 116.00 -96.6900 -130.6987 114.00 -24.6392 -56.5000 114.00 -88.6240 -119.7218 112.00 -22.6060 -51.5000 112.00 -81.2700 -109.7030 110.00 -20.7550 -47.5500 110.00 -74.5700 -100.6170 105.00 -7.6170 -38.4870 105.00 -60.3500 -81.2724 100.00 -13.6900 -31.3000 100.00 -49.0700 -65.9450 95.00 -11.2000 -25.6840 95.00 -40.1000 -53.7603 90.00 -9.2140 -21.1000 90.00 -32.9500 -44.0770 85.00 -7.6170 -17.4250 85.00 -27.3370 -36.3176 80.00 -6.3283 -14.4650 80.00 -22.6950 -30.0751 70.00 -4.4300 -10.1160 70.00 -15.8800 -20.9880 60.00 -3.1525 -7.2000 60.00 -11.3140 -14.8445 50.00 -2.2720 -5.2060 50.00 -8.1950 -10.6612 40.00 -1.6530 -3.8125 40.00 -6.0240 -7.7550 30.00 -1.2085 -2.8200 30.00 -4.4750 -5.6980 20.00 -1.8830 -2.1020 20.00 -3.3570 -4.2240 10.00 -0.6410 -1.5740 10.00 -2.3800 -3.1460 0.00 -0.4590 -1.1800 0.00 -1.9360 -0.3540
Rotation
I= - 6.505 A I= - 15.25 A I= - 24 A I= - 33 A
Theta B Theta B Theta B Theta B
(degree) (G) (degree) (G) (degree) (G) (degree) (G)
0.00 0.0288 0.00 -0.1150 0.00 -0.1540 0.00 -0.2640
55.00 -61.9200 55.00 -148.7800 55.00 -230.0300 55.00 -316.2940
55.50 -68.2600 55.25 -155.1740 55.50 -263.5000 55.25 -332.5850
55.60 -69.6200 55.40 -159.6800 55.40 -248.7940 55.30 -335.9620
55.55 -69.9400 55.45 -161.2270 55.60 -258.7300 55.40 -342.2980
56.00 -75.2000 55.50 -162.7950 55.50 -348.8980
57.00 -91.6000 56.00 -179.4560 56.00 -279.6800 55.60 -355.9930
58.00 -112.0400 57.00 -218.6250 57.00 -341.2300 56.00 384.8570
59.00 -137.5000 58.00 -267.4440 58.00 -417.3400 57.00 -468.7430
60.00 -169.3500 59.00 -328.7500 59.00 -512.4800 58.00 -573.3970
61.00 -208.8200 60.00 -404.8500 60.00 -631.2200 59.00 -704.0110
62.00 -254.4200 61.00 -498.4100 61.00 -777.3000 60.00 -867.4160
63.00 -298.9400 62.00 605.4600 62.00 -944.5000 61.00 -1068.4410
64.00 -327.8700 63.00 -706.3700 63.00 -1102.0000 62.00 1297.4500
65.00 -340.4800 64.00 -771.0200 64.00 -1203.0000 63.00 -1514.5900
66.00 -345.0700 65.00 -299.3600 65.00 -1247.3000 64.00 1653.1900
67.00 -346.7200 66.00 -809.8500 66.00 -1263.7700 65.00 1714.0200
68.00 -347.3000 67.00 -813.6000 67.00 -1269.6000 66.00 1736.4600
69.00 -347.5400 68.00 -814.9900 68.00 -1271.8000 67.00 1744.4900
70.00 -347.6100 69.00 -815.4800 69.00 -1272.6800 68.00 1747.3940
72.00 -347.7000 70.00 -815.6800 70.00 -1273.0000 69.00 -1748.6040
74.00 -347.7800 72.00 -815.8400 72.00 -1273.3000 70.00 1749.0000
76.00 -347.9000 74.00 -816.0100 74.00 -1273.6000 72.00 1749.3300
78.00 -347.9200 76.00 -816.2300 76.00 -1273.9500 74.00 -1749.7370
80.00 -348.0000 78.00 -816.4200 78.00 -1274.2700 76.00 -1750.1000
82.00 -348.0200 80.00 -816.5400 80.00 -1274.5000 78.00 -1750.4300
84.00 0.0500 82.00 -816.6400 82.00 -1274.7000 80.00 -1750.6940
86.00 -348.0700 84.00 -816.7200 84.00 -1274.8700 82.00 -1751.0460
88.00 -348.1000 86.00 -816.8700 86.00 -1275.1000 84.00 -1751.2660
90.00 -348.1200 88.00 -817.0000 88.00 -1275.3500 86.00 -1751.5740
92.00 -348.1200 90.00 -817.0800 90.00 -1275.5000 88.00 -1751.8930
94.00 -348.1300 92.00 -817.1700 92.00 -1275.6000 90.00 -1752.0800
96.00 -348.1200 94.00 -817.2500 94.00 -1275.7700 92.00 -1752.2120
98.00 -348.1000 96.00 -817.3100 96.00 -1275.9000 94.00 -1752.3660
100.00 -348.0700 98.00 -817.3200 98.00 -1275.8500 96.00 -1752.4760
102.00 -348.0400 100.00 -817.2600 100.00 -1275.7600 98.00 -1752.4210
103.00 -348.0100 102.00 -817.2100 102.00 -1275.6000 100.00 -1752.2230
104.00 -347.9200 103.00 -817.1200 103.00 -1275.4500 102.00 -1752.0030
105.00 -347.6700 104.00 -816.9100 104.00 -1275.1100 103.00 -1751.8050
106.00 -346.8200 105.00 -816.2700 105.00 104.00 -1751.3320
107.00 -343.8600 106.00 -813.9200 106.00 -1270.3000 105.00 -1749.8250
108.00 -334.4600 107.00 -805.8400 107.00 -1257.6000 106.00 -1744.7540
109.00 -303.6700 108.00 -778.4700 108.00 -1214.5200 107.00 -1727.3300
109.50 -280.2300 109.00 -704.9500 109.00 -1099.7000 108.00 -1668.2600
110.00 -253.5100 109.50 -648.9400 109.50 -1012.5200 108.50 1604.0420
110.50 -226.2950 110.00 -587.0300 110.00 -915.9200 109.00 -1510.1900
111.00 -201.0330 110.50 -524.0800 110.50 -817.5300 109.50 1389.5200
112.00 -156.6420 111.00 -465.1000 111.00 -725.0000 110.00 -1256.9700
113.00 -122.1500 112.00 -362.9700 112.00 -565.5800 110.50 -1122.2200
113.50 -108.0300 113.00 -283.0300 113.00 -440.9100 111.00 -996.0170
114.00 -95.7700 112.00 -777.0400
115.00 -75.4300 114.00 -221.4100 114.00 -345.2400 113.00 -605.7040
116.00 -59.7560 115.00 -174.4670 115.00 -272.1800 113.50 -535.4470
116.25 -56.3900 116.00 -138.0970 116.00 -214.8900 114.00 -474.2650
116.30 -55.7380 116.25 -130.2390 116.25 -202.6770 115.00 -373.6700
116.40 -54.4500 116.30 -128.6700 116.30 -200.3710 116.25 -295.8560
116.35 -55.0800 116.40 -125.6880 116.40 -195.7000 116.30 -275.3740
116.33 -55.3180 116.50 -122.7610 116.50 -191.1400 116.35 -272.1400
180.00 -0.1100 180.00 -0.1970 117.00 -170.1670 116.40 -268.9280
180.00 -0.1900 116.50 -262.6151
116.60 -256.8720
117.00 -233.8292
180.00 -0.2970
Mapping Origin
File:Hrrl wiki dipole map Origin File.txt
Mapping data and are under the curve
-6.5 A
Mapping at -6.5 Amp.
S B mm G Beam Magnetic Path Field 0 -5.996 5 -7.024 10 -8.265 15 -9.766 20 -11.596 25 -13.836 30 -16.596 35 -20.011 40 -24.25 45 -29.55 50 -35.96 55 -44.25 60 -54.67 65 -67.776 70 -84.225 75 -104.806 80 -130.495 85 -162.485 90 -202.426 92 -221.08 94 -241.527 96 -263.96 98 -288.57 100 -315.31 102 -344.89 104 -377.23 105.11 -395.22 107.9 -447.35 110.68 -505.17 113.46 -576.45 116.24 -629.02 119.02 -686.3 121.81 -733.05 124.59 -766.68 127.37 -788.63 132.94 -809.26 138.5 -815.77 144.07 -817.76 149.63 -818.35 155.2 -818.59 166.33 -818.79 177.46 -819.04 188.58 -819.25 199.71 -819.45 210.84 -819.59 221.97 -819.72 233.1 -819.86 244.23 -820 255.36 -820.16 266.49 -820.3 277.62 -820.4 288.75 -820.43 294.32 -820.4 305.44 -820.38 311.01 -820.24 316.57 -819.74 322.14 -817.73 324.92 -815.06 327.7 -809.82 330.49 -799.64 333.27 -780.86 336.05 -749.13 338.83 -700.97 341.62 -639.14 344.4 -570.24 347.18 -500.24 349.96 -435.41 352.75 -377.2 355.53 -326.14 356.53 -305.79 358.53 -275.51 360.53 -248.38 362.53 -224.38 365.53 -192.56 368.53 -165.48 371.53 -142.4 372.53 -135.47 377.53 -105.75 382.53 -82.85 387.53 -65.196 392.53 -51.56 397.53 -41.05 402.53 -32.897 412.53 -21.705 422.53 -14.625 447.53 -6.12 472.53 -2.94
Area under the curve
[4/18/2012 01:47 "" (2456035)] integ1 Input iy = [Book1]6A!(A"S",B"B") type = 0 (math:Mathematical Area) plot = 0 Output oy = [Book1]6A!(,C"Integrated Y1") x1 = 0 x2 = 472.53 i1 = 1 i2 = 85 area = -90700.3274 y0 = -353.05 x0 = 272.06 dx = 245.38386115956
-15.25 A
Mapping at -15.25 Amp.
S B mm G Beam Magnetic Path Field 0 -5.996 5 -7.024 10 -8.265 15 -9.766 20 -11.596 25 -13.836 30 -16.596 35 -20.011 40 -24.25 45 -29.55 50 -35.96 55 -44.25 60 -54.67 65 -67.776 70 -84.225 75 -104.806 80 -130.495 85 -162.485 90 -202.426 92 -221.08 94 -241.527 96 -263.96 98 -288.57 100 -315.31 102 -344.89 104 -377.23 105.11 -395.22 107.9 -447.35 110.68 -505.17 113.46 -576.45 116.24 -629.02 119.02 -686.3 121.81 -733.05 124.59 -766.68 127.37 -788.63 132.94 -809.26 138.5 -815.77 144.07 -817.76 149.63 -818.35 155.2 -818.59 166.33 -818.79 177.46 -819.04 188.58 -819.25 199.71 -819.45 210.84 -819.59 221.97 -819.72 233.1 -819.86 244.23 -820 255.36 -820.16 266.49 -820.3 277.62 -820.4 288.75 -820.43 294.32 -820.4 305.44 -820.38 311.01 -820.24 316.57 -819.74 322.14 -817.73 324.92 -815.06 327.7 -809.82 330.49 -799.64 333.27 -780.86 336.05 -749.13 338.83 -700.97 341.62 -639.14 344.4 -570.24 347.18 -500.24 349.96 -435.41 352.75 -377.2 355.53 -326.14 356.53 -305.79 358.53 -275.51 360.53 -248.38 362.53 -224.38 365.53 -192.56 368.53 -165.48 371.53 -142.4 372.53 -135.47 377.53 -105.75 382.53 -82.85 387.53 -65.196 392.53 -51.56 397.53 -41.05 402.53 -32.897 412.53 -21.705 422.53 -14.625 447.53 -6.12 472.53 -2.94
Area under the curve
[4/18/2012 02:17 "" (2456035)] integ1 Input iy = [Book1]15A!(A"S",B"B") type = 0 (math:Mathematical Area) plot = 0 Output oy = [Book1]15A!(,C"Integrated Y1") x1 = 0 x2 = 472.53 i1 = 1 i2 = 87 area = -210413.9633 y0 = -820.43 x0 = 288.75 dx = 245.25506096565
24 A
Mapping at - 24 A Amp.
S B mm G Beam Magnetic Path Field 0 -9.243 5 -10.843 10 -12.773 15 -15.12 20 -17.98 25 -21.488 30 -25.808 35 -30.97 40 -37.575 45 -45.83 50 -56.175 55 -69.179 60 -85.536 65 -106.117 70 -131.394 75 -164.266 80 -204.61 85 -254.866 90 -317.34 92 -346.6 94 -378.67 96 -413.85 98 -452.39 100 -494.75 102 -541.15 104 -591.94 105.11 -615.64 107.9 -696.51 110.68 -787.1 113.46 -884.2 116.24 -979.92 119.02 -1069.3 121.81 -1142.4 124.59 -1195 127.37 -1229.2 130.15 -1249.7 132.94 -1261.3 138.5 -1271.5 144.07 -1274.7 149.63 -1275.7 155.2 -1276.2 166.33 -1276.7 177.46 -1277 188.58 -1277.5 199.71 -1277.9 210.84 -1278.2 221.97 -1278.4 233.1 -1278.7 244.23 -1279 255.36 -1279.2 266.49 -1279.44 277.62 -1279.56 288.75 -1279.52 294.32 -1279.46 299.88 -1279.4 305.44 -1279.26 311.01 -1279 316.57 -1278.17 322.14 -1275 324.92 -1270.8 327.7 -1262.6 330.49 -1246.67 333.27 -1217.4 336.05 -1167.8 338.83 -1092.5 341.62 -996.14 344.4 -888.66 347.18 -779.86 349.96 -679.2 352.75 -588.1 355.53 -508.2 356.53 -481.38 358.53 -433.77 360.53 -391.15 362.53 -353 365.53 -302.89 368.53 -260.44 371.53 -224.09 372.53 -213.18 377.53 -166.37 382.53 -130.298 387.53 -102.48 392.53 -81.009 397.53 -64.45 402.53 -51.6 412.53 -33.78 422.53 -22.83 447.53 -9.45 472.53 -4.46
Area under the curve
[4/18/2012 02:22 "" (2456035)] integ1 Input iy = [Book1]24A!(A"S",B"B") type = 0 (math:Mathematical Area) plot = 0 Output oy = [Book1]24A!(,C"Integrated Y1") x1 = 0 x2 = 472.53 i1 = 1 i2 = 89 area = -328194.84795 y0 = -1279.56 x0 = 277.62 dx = 245.22443902201
33 A
Mapping at - 33 Amp.
S B mm G Beam Magnetic Path Field 0 -11.425 5 -13.417 10 -15.828 15 -18.25 20 -22.315 25 -26.683 30 -31.873 35 -38.504 40 -46.74 45 -57.044 50 -69.95 55 -86.175 60 -106.593 65 -132.263 70 -164.517 75 -204.863 80 -255.216 85 -317.7 90 -395.93 92 -432.4 94 -472.48 96 -516.44 98 -564.64 100 -617.51 102 -675.33 104 -738.69 105.11 -767.57 107.9 -868.32 110.68 -980.56 113.46 -1101.2 116.24 -1220.8 119.02 -1331.6 121.81 -1422.5 124.59 -1487.8 127.37 -1530.3 130.15 -1558.4 132.94 -1570.3 138.5 -1582.9 144.07 -1586.9 149.63 -1588.2 155.2 -1588.74 166.33 -1589.3 177.46 -1589.8 188.58 -1590.37 199.71 -1590.73 210.84 -1591.05 221.97 -1591.4 233.1 -1591.8 244.23 -1592.07 255.36 -1592.3 266.49 -1592.4 277.62 -1592.7 288.75 -1592.7 294.32 -1592.6 299.88 -1592.46 305.44 -1592.3 311.01 -1592 316.57 -1590.9 322.14 -1586.97 324.92 -1581.7 327.7 -1571.5 330.49 -1551.8 333.27 -1515.25 336.05 -1453.6 338.83 -1360 341.62 -1239.46 344.4 -1105.5 347.18 -969.8 349.96 -844.62 352.75 -732.05 355.53 -632.51 356.53 -597.3 358.53 -538.2 360.53 -485.2 362.53 -437.7 365.53 -375.37 368.53 -322.4 371.53 -277.28 372.53 -263.9 377.53 -205.84 382.53 -161.1 387.53 -126.58 392.53 -99.94 397.53 -79.38 402.53 -63.56 412.53 -41.35 422.53 -27.64 447.53 -11.3 472.53 -5.193
Area under the curve
[4/18/2012 02:23 "" (2456035)] integ1 Input iy = [Book1]30A!(A"S",B"B") type = 0 (math:Mathematical Area) plot = 0 Output oy = [Book1]30A!(,C"Integrated Y1") x1 = 0 x2 = 472.53 i1 = 1 i2 = 89 area = -408481.827 y0 = -1592.7 x0 = 277.62 dx = 245.24936698806
Effective B-Field
Effective B-field = (Area Under the Curve) / (Beam path in dipole)
| Scan Current | Area Under the Curve (G*mm) | Beam path in dipole (mm) | Effective B-field (G) | |
| -6.50A | -90700.3274 | 250.149315 | -362.584752 | |
| -15.25A | -210413.9633 | 250.149315 | -841.153466 | |
| -24A | -328194.84795 | 250.149315 | -1 311.99579 | |
| -33 A | -408481.827 | 250.149315 | -1 632.95201 |
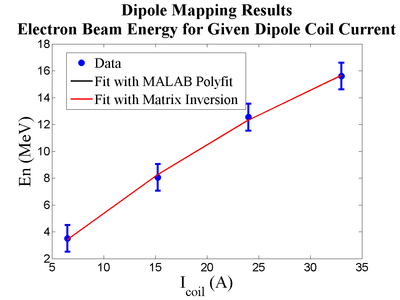
Coil current vs Electron Beam Energy
Magnet (or momentum) rigidity:
p is momentum of the particle. q is the charge of the particle. is the bending radius of the dipole. B is magnetic filed strength.
For an electron
1 Gauss is Tesla
| Coil Current (Amp) | dipole (m) | Effective B-field (T) | P [MeV/c] |
| -6.50 | 0.3185 | -0.0362584752 | 3.46210054 |
| -15.25 | 0.3185 | -0.0841153466 | 8.03166116 |
| -24 | 0.3185 | -0.131199579 | 12.5274472 |
| -33 | 0.3185 | -0.163295201 | 15.5920623 |
| Coil Current (Amp) | P [MeV/c] | En using field map (MeV) | Corresponding En from table (MeV) |
| -6.50 | 3.46210054 | 3.49960871 | 2.403 |
| -15.25 | 8.03166116 | 8.04790047 | (6.129+6.350)/2 |
| -24 | 12.5274472 | 12.5378648 | 10.095 |
| -33 | 15.5920623 | 15.6004336 | 14.064 |
Coil En Current (Amp) (MeV) 6.50 3.49960871 15.25 8.04790047 24 12.5378648 33 15.6004336
Fitting for En vs I
matlab Poly fit method
S =
R: [3x3 double]
df: 1
normr: 0.3244
table =
6.5000 3.4996 3.4261 0.0735 15.2500 8.0479 8.2673 -0.2194 24.0000 12.5379 12.3216 0.2163 33.0000 15.6004 15.6708 -0.0704
MATLAB Polyfit Fit for En vs I: En = 0.66503 + 0.66503I + -0.00514I^2
Matrix Inversion Method
Matrix Inversion Method Fit for En vs I: En = (-0.67944+-2.18159) + (0.66503+-0.25773)I + (-0.00514+-0.00639)I^2
average of two method
0.014 + (0.665+-0.258)I + (-0.00514+-0.00639)I^2
Estimation for En vs I
Current (A) Energy (MeV)
0.1 0.080
0.2 0.147
0.3 0.213
0.4 0.279
0.5 0.345
0.6 0.411
0.7 0.477
0.8 0.543
0.9 0.608
1 0.674
1.1 0.739
1.2 0.805
1.3 0.870
1.4 0.935
1.5 1.000
1.6 1.065
1.7 1.130
1.8 1.194
1.9 1.259
2 1.323
2.1 1.388
2.2 1.452
2.3 1.516
2.4 1.580
2.5 1.644
2.6 1.708
2.7 1.772
2.8 1.836
2.9 1.899
3 1.963
3.1 2.026
3.2 2.089
3.3 2.153
3.4 2.216
3.5 2.279
3.6 2.341
3.7 2.404
3.8 2.467
3.9 2.529
4 2.592
4.1 2.654
4.2 2.716
4.3 2.778
4.4 2.840
4.5 2.902
4.6 2.964
4.7 3.026
4.8 3.088
4.9 3.149
5 3.211
5.1 3.272
5.2 3.333
5.3 3.394
5.4 3.455
5.5 3.516
5.6 3.577
5.7 3.638
5.8 3.698
5.9 3.759
6 3.819
6.1 3.879
6.2 3.939
6.3 3.999
6.4 4.059
6.5 4.119
6.6 4.179
6.7 4.239
6.8 4.298
6.9 4.358
7 4.417
7.1 4.476
7.2 4.536
7.3 4.595
7.4 4.654
7.5 4.712
7.6 4.771
7.7 4.830
7.8 4.888
7.9 4.947
8 5.005
8.1 5.063
8.2 5.121
8.3 5.179
8.4 5.237
8.5 5.295
8.6 5.353
8.7 5.410
8.8 5.468
8.9 5.525
9 5.583
9.1 5.640
9.2 5.697
9.3 5.754
9.4 5.811
9.5 5.868
9.6 5.924
9.7 5.981
9.8 6.037
9.9 6.094
10 6.150
10.1 6.206
10.2 6.262
10.3 6.318
10.4 6.374
10.5 6.430
10.6 6.485
10.7 6.541
10.8 6.596
10.9 6.652
11 6.707
11.1 6.762
11.2 6.817
11.3 6.872
11.4 6.927
11.5 6.982
11.6 7.036
11.7 7.091
11.8 7.145
11.9 7.200
12 7.254
12.1 7.308
12.2 7.362
12.3 7.416
12.4 7.470
12.5 7.523
12.6 7.577
12.7 7.630
12.8 7.684
12.9 7.737
13 7.790
13.1 7.843
13.2 7.896
13.3 7.949
13.4 8.002
13.5 8.055
13.6 8.107
13.7 8.160
13.8 8.212
13.9 8.264
14 8.317
14.1 8.369
14.2 8.421
14.3 8.472
14.4 8.524
14.5 8.576
14.6 8.627
14.7 8.679
14.8 8.730
14.9 8.781
15 8.833
15.1 8.884
15.2 8.934
15.3 8.985
15.4 9.036
15.5 9.087
15.6 9.137
15.7 9.188
15.8 9.238
15.9 9.288
16 9.338
16.1 9.388
16.2 9.438
16.3 9.488
16.4 9.538
16.5 9.587
16.6 9.637
16.7 9.686
16.8 9.735
16.9 9.784
17 9.834
17.1 9.883
17.2 9.931
17.3 9.980
17.4 10.029
17.5 10.077
17.6 10.126
17.7 10.174
17.8 10.222
17.9 10.271
18 10.319
18.1 10.367
18.2 10.414
18.3 10.462
18.4 10.510
18.5 10.557
18.6 10.605
18.7 10.652
18.8 10.699
18.9 10.746
19 10.793
19.1 10.840
19.2 10.887
19.3 10.934
19.4 10.981
19.5 11.027
19.6 11.073
19.7 11.120
19.8 11.166
19.9 11.212
20 11.258
20.1 11.304
20.2 11.350
20.3 11.395
20.4 11.441
20.5 11.486
20.6 11.532
20.7 11.577
20.8 11.622
20.9 11.667
21 11.712
21.1 11.757
21.2 11.802
21.3 11.847
21.4 11.891
21.5 11.936
21.6 11.980
21.7 12.024
21.8 12.068
21.9 12.112
22 12.156
22.1 12.200
22.2 12.244
22.3 12.287
22.4 12.331
22.5 12.374
22.6 12.418
22.7 12.461
22.8 12.504
22.9 12.547
23 12.590
23.1 12.633
23.2 12.675
23.3 12.718
23.4 12.761
23.5 12.803
23.6 12.845
23.7 12.887
23.8 12.929
23.9 12.971
24 13.013
24.1 13.055
24.2 13.097
24.3 13.138
24.4 13.180
24.5 13.221
24.6 13.262
24.7 13.304
24.8 13.345
24.9 13.386
25 13.427
25.1 13.467
25.2 13.508
25.3 13.548
25.4 13.589
25.5 13.629
25.6 13.669
25.7 13.710
25.8 13.750
25.9 13.790
26 13.829
26.1 13.869
26.2 13.909
26.3 13.948
26.4 13.988
26.5 14.027
26.6 14.066
26.7 14.105
26.8 14.144
26.9 14.183
27 14.222
27.1 14.261
27.2 14.299
27.3 14.338
27.4 14.376
27.5 14.414
27.6 14.453
27.7 14.491
27.8 14.529
27.9 14.566
28 14.604
28.1 14.642
28.2 14.679
28.3 14.717
28.4 14.754
28.5 14.792
28.6 14.829
28.7 14.866
28.8 14.903
28.9 14.940
29 14.976
29.1 15.013
29.2 15.049
29.3 15.086
29.4 15.122
29.5 15.158
29.6 15.195
29.7 15.231
29.8 15.266
29.9 15.302
30 15.338
30.1 15.374
30.2 15.409
30.3 15.445
30.4 15.480
30.5 15.515
30.6 15.550
30.7 15.585
30.8 15.620
30.9 15.655
31 15.689
31.1 15.724
31.2 15.759
31.3 15.793
31.4 15.827
31.5 15.861
31.6 15.895
31.7 15.929
31.8 15.963
31.9 15.997
32 16.031
32.1 16.064
32.2 16.098
32.3 16.131
32.4 16.164
32.5 16.197
32.6 16.230
32.7 16.263
32.8 16.296
32.9 16.329
33 16.362
33.1 16.394
33.2 16.426
33.3 16.459
33.4 16.491
33.5 16.523
33.6 16.555
33.7 16.587
33.8 16.619
33.9 16.651
34 16.682
34.1 16.714
34.2 16.745
34.3 16.776
34.4 16.808
34.5 16.839
34.6 16.870
34.7 16.900
34.8 16.931
34.9 16.962
35 16.993
35.1 17.023
35.2 17.053
35.3 17.084
35.4 17.114
35.5 17.144
35.6 17.174
35.7 17.204
35.8 17.233
35.9 17.263
36 17.293
36.1 17.322
36.2 17.351
36.3 17.381
36.4 17.410
36.5 17.439
36.6 17.468
36.7 17.496
36.8 17.525
36.9 17.554
37 17.582
37.1 17.611
37.2 17.639
37.3 17.667
37.4 17.695
37.5 17.723
37.6 17.751
37.7 17.779
37.8 17.807
37.9 17.834
38 17.862
38.1 17.889
38.2 17.917
38.3 17.944
38.4 17.971
38.5 17.998
38.6 18.025
38.7 18.051
38.8 18.078
38.9 18.105
39 18.131
39.1 18.157
39.2 18.184
39.3 18.210
39.4 18.236
39.5 18.262
39.6 18.288
39.7 18.313
39.8 18.339
39.9 18.365
40 18.390
40.1 18.415
40.2 18.441
40.3 18.466
40.4 18.491
40.5 18.516
40.6 18.540
40.7 18.565
40.8 18.590
40.9 18.614
41 18.639
41.1 18.663
41.2 18.687
41.3 18.711
41.4 18.735
41.5 18.759
41.6 18.783
41.7 18.807
41.8 18.830
41.9 18.854
42 18.877
42.1 18.900
42.2 18.923
42.3 18.947
42.4 18.970
42.5 18.992
42.6 19.015
42.7 19.038
42.8 19.060
42.9 19.083
43 19.105
43.1 19.127
43.2 19.150
43.3 19.172
43.4 19.194
43.5 19.215
43.6 19.237
43.7 19.259
43.8 19.280
43.9 19.302
44 19.323
44.1 19.344
44.2 19.365
44.3 19.386
44.4 19.407
44.5 19.428
44.6 19.449
44.7 19.469
44.8 19.490
44.9 19.510
45 19.531
45.1 19.551
45.2 19.571
45.3 19.591
45.4 19.611
45.5 19.630
45.6 19.650
45.7 19.670
45.8 19.689
45.9 19.708
46 19.728
46.1 19.747
46.2 19.766
46.3 19.785
46.4 19.804
46.5 19.823
46.6 19.841
46.7 19.860
46.8 19.878
46.9 19.897
47 19.915
47.1 19.933
47.2 19.951
47.3 19.969
47.4 19.987
47.5 20.004
47.6 20.022
47.7 20.040
47.8 20.057
47.9 20.074
48 20.091
48.1 20.109
48.2 20.126
48.3 20.142
48.4 20.159
48.5 20.176
48.6 20.193
48.7 20.209
48.8 20.225
48.9 20.242
49 20.258
49.1 20.274
49.2 20.290
49.3 20.306
49.4 20.322
49.5 20.337
49.6 20.353
49.7 20.368
49.8 20.384
49.9 20.399
50 20.414
50.1 20.429
50.2 20.444
50.3 20.459
50.4 20.474
50.5 20.488
50.6 20.503
50.7 20.517
50.8 20.532
50.9 20.546
51 20.560
51.1 20.574
51.2 20.588
51.3 20.602
51.4 20.615
51.5 20.629
51.6 20.642
51.7 20.656
51.8 20.669
51.9 20.682
52 20.695
52.1 20.708
52.2 20.721
52.3 20.734
52.4 20.747
52.5 20.759
52.6 20.772
52.7 20.784
52.8 20.797
52.9 20.809
53 20.821
53.1 20.833
53.2 20.845
53.3 20.856
53.4 20.868
53.5 20.880
53.6 20.891
53.7 20.902
53.8 20.914
53.9 20.925
54 20.936
54.1 20.947
54.2 20.958
54.3 20.968
54.4 20.979
54.5 20.989
54.6 21.000
54.7 21.010
54.8 21.020
54.9 21.030
55 21.041
55.1 21.050
55.2 21.060
55.3 21.070
55.4 21.080
55.5 21.089
55.6 21.098
55.7 21.108
55.8 21.117
55.9 21.126
56 21.135
56.1 21.144
56.2 21.153
56.3 21.161
56.4 21.170
56.5 21.178
56.6 21.187
56.7 21.195
56.8 21.203
56.9 21.211
57 21.219
57.1 21.227
57.2 21.235
57.3 21.242
57.4 21.250
57.5 21.257
57.6 21.265
57.7 21.272
57.8 21.279
57.9 21.286
58 21.293
58.1 21.300
58.2 21.307
58.3 21.313
58.4 21.320
58.5 21.326
58.6 21.332
58.7 21.339
58.8 21.345
58.9 21.351
59 21.357
59.1 21.362
59.2 21.368
59.3 21.374
59.4 21.379
59.5 21.385
59.6 21.390
59.7 21.395
59.8 21.400
59.9 21.405
60 21.410
60.1 21.415
60.2 21.419
60.3 21.424
60.4 21.428
60.5 21.433
60.6 21.437
60.7 21.441
60.8 21.445
60.9 21.449
61 21.453
61.1 21.457
61.2 21.460
61.3 21.464
61.4 21.467
61.5 21.471
61.6 21.474
61.7 21.477
61.8 21.480
61.9 21.483
62 21.486
62.1 21.489
62.2 21.491
62.3 21.494
62.4 21.496
62.5 21.498
62.6 21.501
62.7 21.503