Sadiq Proposal Defense Jan 2nd 2012

Abstract

We are constructing a achromatic positron source in the Beam Lab of Department of Physics at Idaho State University. We have studied the radiation level after moving the cavity to new location with GEANT4 simulation and experiment. Our conclusion is it was safe to do so. We Constructed new beamline, performed emittance measurements, and we calculated emittance and twiss parameters. We acquired some NaI crystals from Idaho Accelerator Center (IAC). We built our own PMT bases for them by modifying one the design one of the model from Saint-Gobain crystals & detectors ltd. NaI detectors tested and worked properly. A tungsten target will be placed in the space between 1st and 2nd triplet. The tungsten target will be placed inside a big chamber. To do emittance test with precise energy scan, the dipole magnet was remapped. This will also improve our emittance measurement. We are expecting to collect positrons and transport them down the second tungsten target at the end of the 90 degree beamline. By doing these, 511 keV photons will be created and we want to detect them by our NaI detectors.

Introduction

I propose to measure the efficiency of producing positrons using the High Repetition Rate Linac (HRRL) S-band electron linear accelerator. HRRL cavity is located at the Beam Lab of the Physics Department, at Idaho State University (ISU).

HRRL has max beam energy of 16 MeV, max peak current of 80 mA, max repetition rate of 1 kHz, and max pulse length of 250 ns (FWHM).

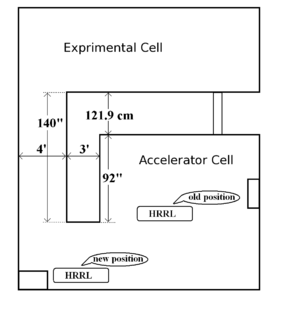
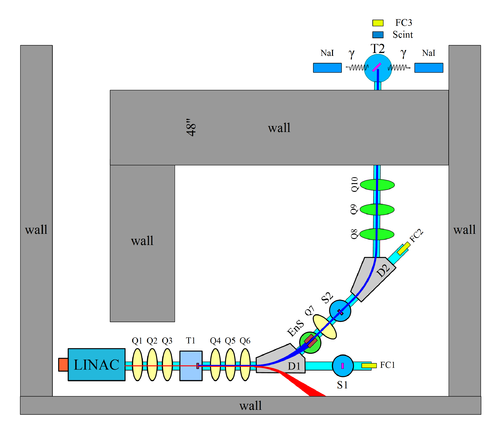
The HRRL facility is divided into two parts by a L-shaped cement wall. The accelerator cell houses the linac and magntic elements needed to transport electrons. The experimental cell is located in an adjacent room to the accelerator cell. Previously cavity was located at the center of the accelerator cell, as shown in figure below. To adapt positron project, it was relocated to new position, as shown in same figure.

Fig. Top view of the HRRL cavity room.

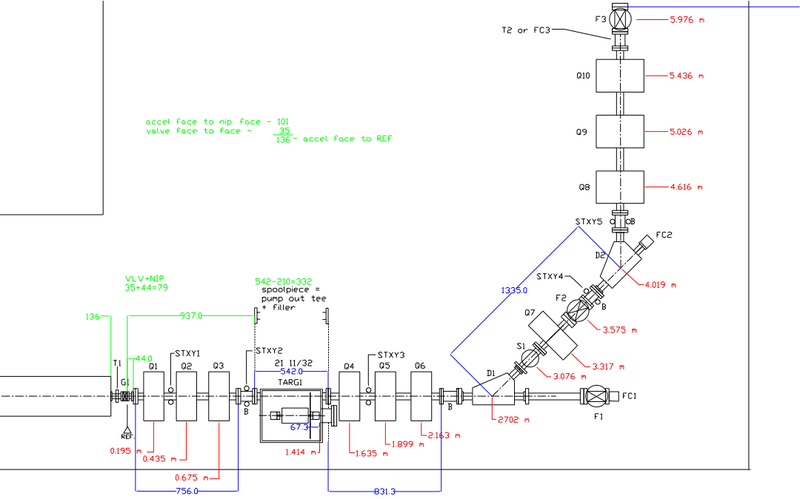
Original HRRL beamline was designed by G. Stancari. Based on this designed, it was improved by Dr. Y. Kim, and was finalized by John Ellis. Design is shown on the following figure.

Fig. Final HRRL beamline by John Ellis.

The beam parts were listed in the following table given by John Ellis.

Label	Beam Line Element	Z location from Gate Valve center of element	Dimensions of Element
T1	Torroid 1	-0.05 m
G1	Fast Gate Valve	0.000 m
STXY1	X-Y steerers 1		want to locate before Q1!
Q1	First Quad	0.195 m	(was moved from 0.175 to 0.195)
Q2	Second Quad	0.435 m	(was moved from 0.425 to 0.435) (24 cm to Q1)
Q3	Third Quad	0.675 m	(24 cm to Q2)
STXY2	X-Y steerers 2
Targ1	positron production target	1.175 m
Q4	Fourth Quad	1.635 m	(was 1.4 now 1.635)
Q5	Fifth Quad	1.659 m	was 1.650 drawing has 1.899 we want it at 1.659 (want distance to Q4 to be 24 cm)
Q6	Sixth Quad	1.683	was at 1.8 drawing has it at 2.163 we want it at 1.683 (want distance to Q5 to be 24 cm)
STXY3	X-Y steerers 3
F1	OTR Flag
FC1	Faraday Cup 1
D1	First Kiwi Dipole	2.702 m	was 2.525 now it is 2.702
S1	Energy Slits	3.076 m	was 2.851 now at 3.076
STXY4	X-Y steerers 4
Q7	Seventh Quad	3.317 m	was at 3.026 now at 3.317
F2	Yag SCREEN	m	attach directly to Dipole D2 and put bellows upstream, drawing has it backwards
D2	Second Kiwi Dipole	4.019 m	was at 3.617 now at 4.019
Q8	Eigth Quad	4.616 m
STXY5	X-Y steerers 5
Q9	Quad	5.026 m
Q10	Quad	5.436 m
T2	Torroid 2
F3	Third Flag	5.976 m
Targ2	Brehm target ladder	m
	HOLE@WALL	6.412 m

Electron beam out of cavity will pass through first set of quadruple triplet magnets, which is going to focus electron beam on the positron target. Positrons created in the target will be collected second set of quadruple triplet, then will be bent 45 degree by first dipole magnet. Positron target can be placed in or removed from beam line, so that we run positron or electron dual mode. Accordingly, we change the polarity of the dipoles to run on e-/e+ modes. The The second dipole will bend beam another 45 degree, thus complete total of 90 degree bend. Third set of quadruple triplet will be used create e-/e+ beam profile that sutable for users' specific need.

Motivation

We want to create positron source at ISU. We also want to study how we can increase the positron to electron ratio.

Emittance

Emittance is an important parameter in accelerator physics. If emittance with twiss parameters are given at the exit of the gun, we will be able to calculate beam size and divergence any point after the exit of the gun. Knowing the beam size and beam divergence on the positron target will greatly help us study the process of creating positron. Emittance with twiss parameters are also key parameters for any accelerator simulations. Also, energy and energy spread of the beam will be measured in the emittance measurement.

What is Emittance

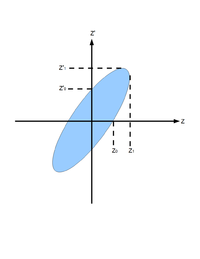
In accelerator physics, Cartesian coordinate system was used to describe motion of the accelerated particles. Usually the z-axis of Cartesian coordinate system is set to be along the electron beam line as longitudinal beam direction. X-axis is set to be horizontal and perpendicular to the longitudinal direction, as one of the transverse beam direction. Y-axis is set to be vertical and perpendicular to the longitudinal direction, as another transverse beam direction.

For the convenience of representation, we use [math]z[/math] to represent our transverse coordinates, while discussing emittance. And we would like to express longitudinal beam direction with [math]s[/math]. Our transverse beam profile changes along the beam line, it makes [math]z[/math] is function of [math]s[/math], [math]z~(s)[/math]. The angle of a accelerated charge regarding the designed orbit can be defined as:

[math]z'=\frac{dz}{ds}[/math]

If we plot [math]z[/math] vs. [math]z'[/math], we will get an ellipse. The area of the ellipse is an invariant, which is called Courant-Snyder invariant. The transverse emittance [math]\epsilon[/math] of the beam is defined to be the area of the ellipse, which contains 90% of the particles <ref name="MConte08"> M. Conte and W. W. MacKay, “An Introduction To The Physics Of Particle Accelera tors”, World Scientifc, Singapore, 2008, 2nd Edition, pp. 257-330. </ref>.

Fig.1 Phase space ellipse <ref name="MConte08"></ref>.

Measurement of Emittance with Quad Scanning Method

In quadrupole scan method, a quadrupole and a Yttrium Aluminum Garnet (YAG ) screen was used to measure emittance. Magnetic field strength of the quadrupole was changed in the process and corresponding beam shapes were observed on the screen. Transfer matrix of a quadrupole magnet under thin lens approximation:

[math] \left( \begin{matrix} 1 & 0 \\ -k_{1}L & 1 \end{matrix} \right)=\left( \begin{matrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{matrix} \right) [/math]

Here, [math]k_{1} L[/math] is quadrupole strength, [math]L[/math] is quadrupole magnet thickness, and f is quadrupole focal length. [math] k_{1} L \gt 0 [/math] for x-plane, and [math] k_{1} L \lt 0 [/math] for y-plane. Transfer matrix of a drift space between quadrupole and screen:

[math] \mathbf{S} = \left( \begin{matrix} S_{11} & S_{12} \\S_{21} & S_{22} \end{matrix} \right)=\left( \begin{matrix} 1 & l \\ 0 & 1 \end{matrix} \right) [/math]

Here, [math]l[/math] ([math]S_{12}[/math]) is the distance from the center of the quadrupole to the screen. Transfer matrix of the scanned region is:

[math] \mathbf{M} = \mathbf{SQ} = \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix}= \begin{pmatrix} S_{11} & S_{12} \\ S_{21} & S_{22} \end{pmatrix} \begin{pmatrix} 1 & 0 \\ -k_1L & 1 \end{pmatrix}= \begin{pmatrix} S_{11} - k_1LS_{12} & S_{12} \\ S_{21} - k_1L S_{22} & S_{22} \end{pmatrix} [/math]

[math]\mathbf{M}[/math] is related with the beam matrix [math]\mathbf{\sigma}[/math] as:

[math] \mathbf{ \sigma_{screen}} = \mathbf{M \sigma_{quad} M^T} = \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix} \begin{pmatrix} \sigma_{quad, 11} & \sigma_{quad, 12} \\ \sigma_{quad, 21} & \sigma_{quad, 22} \end{pmatrix} \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix} [/math]

Since:

[math] \sigma_{x}=\sqrt{\epsilon_x\beta},~\sigma_{x'}=\sqrt{\epsilon_x\gamma},~\sigma_{xx'}={-\epsilon_x\alpha} [/math]

[math] \mathbf{ \sigma} = \begin{pmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{pmatrix} = \begin{pmatrix} \sigma_{x}^2 & \sigma_{xx'} \\ \sigma_{xx'} & \sigma_{x'}^2 \end{pmatrix} [/math]

So, [math]\mathbf{\sigma}[/math] matrix can be written as: [math] \mathbf{\sigma}_{quad} = \begin{pmatrix} \sigma_{quad, x} & \sigma_{quad, xx'} \\ \sigma_{quad, xx'} & \sigma_{quad, x,} \end{pmatrix} = \epsilon_{rms, x} \begin{pmatrix} \beta & -\alpha \\ -\alpha & \gamma \end{pmatrix} [/math]

Substituting this give:

[math] \mathbf{ \sigma_{screen}} = \mathbf{M \sigma_{quad} M^T} = \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix} \epsilon_{rms, x} \begin{pmatrix} \beta & -\alpha \\ -\alpha & \gamma \end{pmatrix} \begin{pmatrix} m_{11} & m_{12} \\ m_{21} & m_{22} \end{pmatrix} [/math]

Dropping off subscript "rms" on emittance [math]\epsilon_{rms, x}[/math]: [math] \sigma_{screen, 11}=\sigma_{screen, x}^2=\epsilon_x (m_{11}^2\beta - 2m_{12}m_{11}\alpha+m_{12}^2\gamma) [/math]

Using [math]\mathbf{\sigma}[/math] matrix relations:

[math] \sigma_{x}={\epsilon_x\beta},~\sigma_{12}={-\epsilon_x\alpha},~{\epsilon_x\gamma}=\epsilon_x \frac{1+\alpha^2}{\beta}=\frac{\epsilon_x^2+\sigma_{12}^2}{\sigma_{11}} [/math]

Here [math]\sigma_{x}[/math] is [math]\sigma_{screen, x}[/math]. We got:

[math] \sigma_{x}^2=m_{11}^2 \sigma_{11} + 2m_{12}m_{11} \sigma_{12} + m_{12}^2 \frac{\epsilon_x^2+\sigma_{12}^2}{\sigma_{11}} [/math]

[math] \sigma_{x}^2=\sigma_{11} \left(m_{11}^2 + 2m_{11}m_{12}\frac{\sigma_{12}}{\sigma_{11} }+ m_{12}^2\frac{\sigma_{12}^2}{\sigma_{11}^2}\right) + m_{12}\frac{\epsilon_x^2}{\sigma_{11}} [/math]

[math] \sigma_{x}^2=\sigma_{11}\left(m_{11} + m_{12}\frac{\sigma_{12}}{\sigma_{11} }\right)^2 + m_{12}\frac{\epsilon_x^2}{\sigma_{11}} [/math]

Recall:

[math] m_{11} = S_{11}-kLS_{12}~~~~~~m_{12}=S_{12} [/math]

Substituting and reorganizing result in:

[math] \sigma_{x}^2=\sigma_{11} {S_{12}^2}\left(kL - \left( \frac{S_{11}}{S_{12}} + \frac{\sigma_{12}}{\sigma_{11}} \right) \right)^2 + S_{12}^2\frac{\epsilon_x^2}{\sigma_{11}} [/math]

Introducing constants [math]A[/math],[math]B[/math], and [math]C[/math]

[math] A = \sigma_{11} {S_{12}^2},~~B = \frac{S_{11}}{S_{12}} + \frac{\sigma_{12}}{\sigma_{11}},~~C = S_{12}^2\frac{\epsilon_x^2}{\sigma_{11}} [/math]

This will simplify equation to:

[math] \sigma_{x}^2=A(kL - B)^2 + C = A(kL)^2 - 2AB(kL)+(C+AB^2) [/math]

It is easy to see that:

[math] \epsilon = \frac{\sqrt{AC}}{S_{12}^2} [/math]

By changing quadrupole magnetic field strength [math]k[/math], we can change beam sizes [math]\sigma_{x,y}[/math] on the screen. We make projection to the x, y axes, then fit them with Gaussian fittings to extract rms beam sizes, then plot vs [math]\sigma_{x,y}[/math] vs [math]k_{1}L[/math]. By Fitting a parabola we can find constants [math]A[/math],[math]B[/math], and [math]C[/math], and get emittances.

First Emittance Measurement Experiment

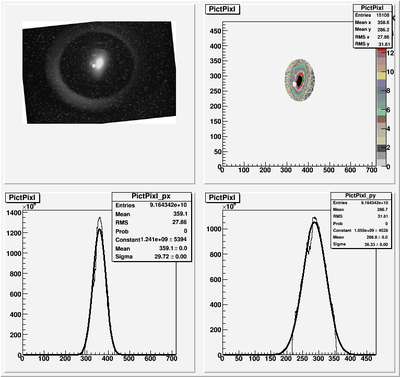
In July 2010y, Emittance measurement of HRRL was conducted at Beam Lab, at Physics Department of ISU. We installed a YAG crystal on the HRRL beam line to see electron beam. A quadrupole magnet was installed between HRRL gun and the YAG screen. We changed current on the quadrupole to control magnetic field strength of the quadrupole magnet, thus we changed electron beam shape on the YAG screen.

Experimental Setup

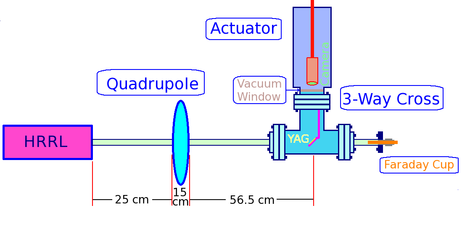
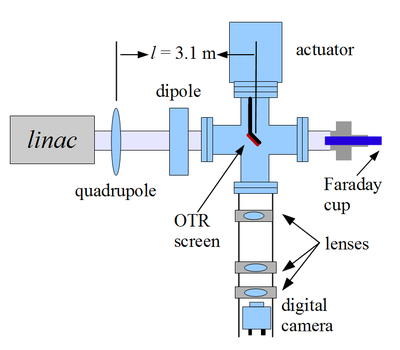
We did quadrupole scan to measure emittance of the electron beam in HRRL. In quadrupole scan method, the strength of the quadrupole magnet was changed by changing the current go through quadrupole coils. The electron beam were coming out of the gun went through quadrupole, then beam would enter a 3-way cross. Two end of the 3-way cross was installed on the beam line. The third end of the 3-way cross was placed upward and there was a actuator installed to it. The YAG crystal was mounted in the actuator, which can put the YAG in the beam line or take it out of the beam line. A camera was placed inside the actuator to look through vacuum a window and to capture the image on the YAG crystal created by electron beam. A Faraday cup was mounted at the end of the beam line to measure the transmission of the charge.

Setup and beam line and are shown in figures 1.2 and 1.3:

Fig.2 Experiment set up of HRRL 2010 July emittance test.

Fig.3 Beam Line of HRRL 2010 July emittance test.

Figures 4, 5, and 6 show Faraday cup, Quadrupole Magnet, and YAG Chrystal used in the test:

Fig.4 Faraday cup used for HRRL 2010 July emittance test.

Fig.5 Quadrupole Magnet used for HRRL 2010 July emittance test.

Fig.6 YAG Christal used for HRRL 2010 July emittance test.

Experiment with YAG

Emittance measurement was carried out on HRRL on July of 2010 under the experimental setup discussed in previous section. In this measurement we used analog camera to take images.

When relativistic electron beam pass through YAG target, Opitcal Transition Radiation (OTR) is produced. OTR are taken for different quadrupole coil current (0-20 A).

Fig. OTR image of 0 Amp quadrupole coil current.	Fig. OTR image of 5 Amp quadrupole coil current.	Fig. OTR image of 10 Amp quadrupole coil current.
Fig. OTR image of 15 Amp quadrupole coil current.	Fig. OTR image of 20 Amp quadrupole coil current.	Fig. OTR image of -10 Amp quadrupole coil current.

Data Analysis

In the mages we can see a bright spot at the center. This spot did not change by changing quad coil current. So, this is image of hot filament. The bigger spot at the right side of the filament was changing by changing quad coil current, hence it is OTR. We also see 10 mm circle mounted on the OTR target, as well as beam hallow.

We did Guassian fits to beam image to extract x, y RMS values for different quad currents. We discovered that the camera was rotated slightly. To compensate for images were rotated, so that we have beam image upright. To reduce back ground, we just focused on OTR beam image and took out the filament spot from data, as shown in image below.

Fig. Gaussian fits for OTR images.

Each image was fitted 7 times, and RMS values are extracted and listed below.

Positive quad coil current

Coild Current (Amps)	Mean and Error
0	[math]{\sigma}_{x,y}= 25.3\pm2.2 , 25.2 \pm1.9 [/math]
1	[math]{\sigma}_{x,y}= 27.5\pm4.6 , 24.8 \pm 2.7 [/math]
2	[math]{\sigma}_{x,y}= 31.4 \pm 6.9 , 23.8 \pm 2.8 [/math]
3	[math]{\sigma}_{x,y}= 35.3 \pm 5.0 , 21.8 \pm 4.7 [/math]
4	[math]{\sigma}_{x,y}= 35.4 \pm 5.5 , 20.0 \pm 4.1 [/math]
5	[math]{\sigma}_{x,y}= 37.0 \pm 4.2 , 17.6 \pm 0.6 [/math]
6	[math]{\sigma}_{x,y}= 38.6 \pm 4.8 , 16.1 \pm 0.4 [/math]
7	[math]{\sigma}_{x,y}= 42.4 \pm 3.8 , 15.4 \pm 0.5 [/math]
8	[math]{\sigma}_{x,y}= 42.4 \pm 2.3 , 15.0 \pm 0.5 [/math]
9	[math]{\sigma}_{x,y}= 42.8 \pm 2.4 , 14.1 \pm 1.2 [/math]
10	[math]{\sigma}_{x,y}= 44.6 \pm 2.2 , 14.4 \pm 0.3 [/math]
11	[math]{\sigma}_{x,y}= 46.6 \pm 0.6 , 13.5 \pm 1.0 [/math]
12	[math]{\sigma}_{x,y}= 47.3 \pm 2.0 , 12.1 \pm 0.5 [/math]
13	[math]{\sigma}_{x,y}= 49.9 \pm 1.0 , 11.6 \pm 0.4 [/math]
14	[math]{\sigma}_{x,y}= 51.5 \pm 0.7 , 11.5 \pm 0.2 [/math]
15	[math]{\sigma}_{x,y}= 51.8 \pm 1.2 , 11.7 \pm 0.3 [/math]
16	[math]{\sigma}_{x,y}= 53.4 \pm 1.1 , 12.3 \pm 0.5 [/math]
17	[math]{\sigma}_{x,y}= 56.5 \pm 0.9 , 13.1 \pm 0.7 [/math]
18	[math]{\sigma}_{x,y}= 56.4 \pm 1.9 , 13.6 \pm 0.4 [/math]
19	[math]{\sigma}_{x,y}= 56.5 \pm 3.0 , 15.0 \pm 0.7 [/math]
20	[math]{\sigma}_{x,y}= 57.8 \pm 2.4 , 18.0 \pm 1.0 [/math]

Negative quad coil current

Coild Current (Amps)	Mean and Error
0	[math]{\sigma}_{x,y}=31.1 \pm 3.1,34.9\pm3.8 [/math]
1	[math]{\sigma}_{x,y}= 25.5 \pm 1.9 , 35.5 \pm 5.1 [/math]
2	[math]{\sigma}_{x,y}= 25.2 \pm 1.5 , 40.1 \pm 6.0 [/math]
3	[math]{\sigma}_{x,y}=23.5 \pm 1.1 , 39.6\pm 2.5 [/math]
4	[math]{\sigma}_{x,y}= 20.4\pm 0.8 , 41.1\pm 2.2 [/math]
5	[math]{\sigma}_{x,y}= 18.0 \pm 0.4 , 46.1 \pm 2.7 [/math]
6	[math]{\sigma}_{x,y}= 16.2 \pm 0.3 , 49.2\pm 1.6 [/math]
7	[math]{\sigma}_{x,y}= 13.3\pm0.4 , 47.8\pm 2.1 [/math]
8	[math]{\sigma}_{x,y}= 12.3\pm 0.5 , 48.4 \pm 1.7 [/math]
9	[math]{\sigma}_{x,y}= 13.3 \pm 0.1 ,53.0 \pm 2.0 [/math]
10	[math]{\sigma}_{x,y}= 12.6 \pm 0.3 , 55.6 \pm 1.9 [/math]
11	[math]{\sigma}_{x,y}= 10.1 \pm 0.4 ,54.4 \pm 2.4 [/math]
12	[math]{\sigma}_{x,y}= 10.8\pm 0.9, 57.3\pm1.8 [/math]
13	[math]{\sigma}_{x,y}= 8.9 \pm 0.2 , 56.8 \pm 2.3 [/math]
14	[math]{\sigma}_{x,y}= 10.7 \pm 0.2 , 58.5\pm 2.3 [/math]
15	[math]{\sigma}_{x,y}= 10.5 \pm 0.3 , 57.5 \pm 1.8 [/math]
16	[math]{\sigma}_{x,y}= 11.3 \pm 0.4 , 59.4 \pm 2.9 [/math]
17	[math]{\sigma}_{x,y}= 12.2 \pm 0.7 , 59.6 \pm 2.6 [/math]
18	[math]{\sigma}_{x,y}= 12.4 \pm 0.6 , 59.0\pm 1.7 [/math]
19	[math]{\sigma}_{x,y}= 13.5 \pm 2.7 , 57.8 \pm 2.9 [/math]
20	[math]{\sigma}_{x,y}= 13.8 \pm 1.5 , 60.3 \pm 2.0 [/math]
22	[math]{\sigma}_{x,y}= 13.3 \pm 2.4 , 59.8 \pm 2.1 [/math]

Now, we need to convert pixels to physical length. Diameter of circle inside YAG crystal is 10 mm. Dividing 10 mm by the pixel numbers of the circle will give us conversion factor.

Average Horizontal Diameter (pixels)	Average Vertical Diameter (pixels)
[math] 90.29 \pm 0.49 [/math]	[math] 59.43 \pm 0.53 [/math]
Horizontal mm/pixels	Vertical mm/pixels
[math] 0.1108 \pm 0.0006 [/math]	[math] (0.1683 \pm 0.0015)*cos45^{o} [/math] = [math] 0.1190\pm 0.0011 [/math]

Magnetic coil current relation to the B-filed at the center of the quad was measured to be:

[math] B(I) = (3.6 \pm 1.3) \times 10^{-3} + (1945 \pm 2) \times 10^{-5} I [kG] = (3.6 \pm 1.3) \times 10^{-4} + (1945 \pm 2) \times 10^{-6} I [T] [/math]

Quadrupole Strength is defined as:

[math] k = 0.2998 \frac{g[T/m]}{p[GeV]} [/math]

g here is the gradient of the qudrupole. p is the momentum of the e- beam. In our case, energy of the beam is 0.01 GeV and gap between dipole center and pole face is 1 inch.

[math] k = 0.2998 \frac{\frac{B(I)}{(1 inch)\times\frac{1 m}{1 inch}}[T/m]}{0.01 GeV} [/math]

Subsituting [math] B(I) [/math] with current. So,

[math] k = 0.2998 \frac{ (3.6 \pm 1.3) \times 10^{-4} + (1945 \pm 2) \times 10^{-6} I [T] }{0.01 \times 0.0254 [GeV][m]} [/math]

[math] k = (0.42 \pm 0.16) + (2.2956 \pm 0.0024) \times I[/math]

Results

Fig. Square of RMS beam size [math] \sigma_x^2 [/math] vs. quad strength times quad pole length [math] k_1L [/math] for x projection of electron beam profile

Fig. Square of RMS beam size [math] \sigma_x^2 [/math] vs. quad strength times quad pole length [math] k_1L [/math] for y projection of electron beam profile

[math] \sigma_x^2= (8.05 \pm 0.25) + (4.18 \pm 0.19)k_1L + (0.64 \pm 0.034)(k_1L)^2 [/math]

[math] \epsilon_x = 2.2 \pm 1.3~mm*mrad ~\Rightarrow~ \epsilon_{n,x} = 42.4 \pm 25.4~mm*mrad[/math]

[math] \beta_x=0.72 \pm 0.31, \alpha_x=-1.23 \pm 0.56 [/math]

[math]\sigma_y^2 = (8.52 \pm 0.40) + (-3.88 \pm 0.28)k_1L + (0.57 \pm 0.048)(k_1L)^2 [/math]

[math] \epsilon_y = 2.6 \pm 2.0~mm*mrad ~\Rightarrow~ \epsilon_{n,y} = 50.5 \pm 38.3~mm*mrad[/math]

[math] \beta_y=0.54 \pm 0.22, \alpha_y=2.68 \pm 1.13 [/math]

Effective length

Second Emittance Measurement Experiment

During first emittance measurement, we see our electron beam image at YAG crystal is much bigger than expected. Comparison study shows that for same beam YAG screen shows bigger beam size than Optical Transition Radiation (OTR) screen. Yag is good for low charge beam. Electron beam from HRRL has a big charge in a single pulse and beam size is big.

We did out second emittance measurement with 10 [math]\mu m[/math] thick aluminium OTR screen. We also improved our optical imaging system by using better digital camera that can be triggered by the same pulse trigger electron gun and also by using three 2 inch diameter lenses to focus the lights from OTR to the CCD of the camera.

Experimental Setup

The cavity was moved the new location and beam line was built by the design of Dr. Yujong Kim, as shown in figure

Fig. HRRL beamline

Experimental setup is shown in the following figure

Fig. HRRL beamline

We chose one of the quad at a time to do the scan and turned off all the other quads. Optical transition radiation was observed at OTR target. At the end of 0 degree beamline we have a Faraday cup to measure the charge of the beam. Camera cage system was located below the OTR target. There are 3 lenses used to focus lights from target to the CCD camera. Target can be pushed into or taken out of the beamline by the actuator at the top.

Fig. HRRL beamline: Cavity and first triplet (Q1, Q2, and Q3).	Fig. HRRL beamline: First triplet and second triplet (Q4, Q5, and Q6).
Fig. HRRL beamline: First Diploe (D1), Quad 7 (Q7), and second dipole (D2).	Fig. HRRL beamline: 90 degree beamline.
Fig. HRRL beamline: Third triplet (Q8, Q9, Q10).	Fig. HRRL beamline: Faraday cup at the end of the 0 degree beamline.
Fig. HRRL beamline: View of the 6-way cross holder and OTR target in the 6-way cross.	Fig. HRRL beamline: Close view of the OTR target in the 6-way cross
Fig. HRRL beamline: Jlab actuator to insert or remove OTR target from the beamline.	Fig. HRRL beamline: Cage system for camera. Camera is at the bottom.

We chose one of the quad at a time to do the scan and turned off all the other quads. Optical transition radiation was observed at OTR target. At the end of 0 degree beamline we also have a Faraday cup to measure the charge of the beam.

OTR Target can be pushed into or taken out of the beamline vertically by the actuator at the top, which is attached to the 6-way cross. This actuator controlled remotely at the control desk.

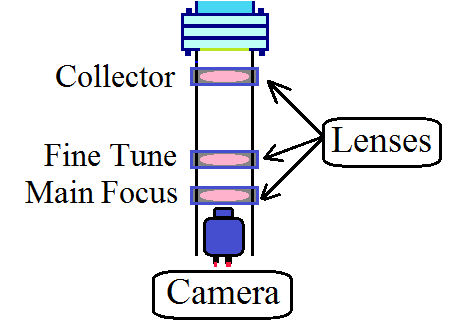
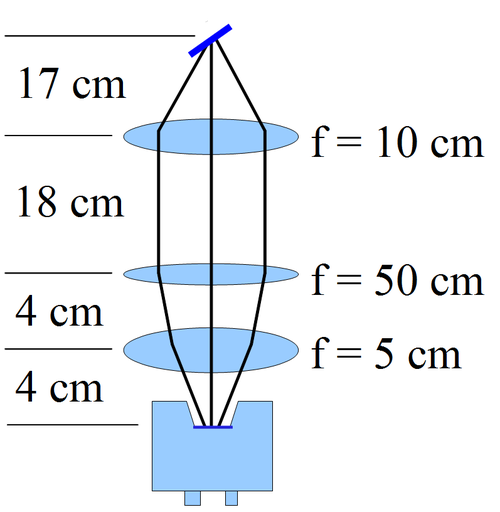
Camera cage system was located below the OTR target. Cage system attached to the bottom of the 6-way cross, and where there is a transparent window. There are 3 lenses used to focus lights from target to the CCD camera. They have focal length of 100 mm, 500 mm, and 50 mm.

The lens closest to the OTR target is 10 cm away from the target, an it has 100 mm focal length. This lens was located as close to the target as possible, so that we might collect as much OTR light as possible, and it was thus called collector lens. The lens in the middle has focal length of 500 mm. Moving this lens will change total focal length in a small amount, and this allow us to do fine tuning. Thus, we called this lens fine tuning lens. The last lens, which is furthest from target, and closed to the CCD camera has the shortest focal length of 5o mm. Its short focal length allow us to focus the light on the very small sensing area of the CCD camera.

Fig. HRRL beamline: Optical cage system to focus OTR lights on CCD camera.

Fig. HRRL beamline: Optical lenses lay out for optical cage system.

Experiment with OTR

Optical Transition Radiation (OTR): Transition radiation is emitted when a charge moving at a constant velocity cross a boundary between two materials with different dielectric constant.

Emittance measurement was carried out on HRRL on March of 2011 under the experimental setup discussed in previous section. In this measurement we used JAI digital camera.

When relativistic electron beam pass through Aluminum target OTR is produced. OTR are taken for different quadrupole coil currents.

Fig. OTR image of 0 Amp Q1 coil current.

Fig. OTR image of +1 Amp Q1 coil current.

Fig. OTR image of +2 Amp Q1 coil current.

Tuning HRRL

When we turned on the HRRL, we put the beam at the center of the screen by steerers. When we tried to do the quad scan, we noticed electron beam was steered by the quad. This could be the result of off-centered electron beam. We tried to center electron beam by tuning HRRL. We can paly with electron gun steering magnets (vertical and horizontal) and cavity out up steering magnets (vertical and horizontal). We have gun solenoid and cavity out up solenoid to play with.

Looking at the beam position on the screen and by the beam current on FC, we tried to align beam line. The goal was to center the beam on the center of the screen, and maximize the FC charge as high as we can.

To maximize the charge and to position the beam image at the center of the screen, the vacuum pipes and the first dipole were realigned.

On March 16th, 2011, we reduced the mis-steering at the quadrupole by tuning steerers in the linac.

By Dr. Kim

On March 17th Dr. Kim tuned HRRL. We used Q1 to do the scan, and we noticed that steering of the beam by the quadruple is unnoticeable. Following table shows the parameter after his tuning.

Solenoid 1	6.8 A
Solenoid 2	10.4 A
Gun Ver	-0.2 A
Gun Hor	+0.4 A
Output Hor	-1.4A
Output Ver	-0.5 A
Gun HV	+9.75 (Knob Setting)
Gun Grid Voltage	5.25 (Knob Setting)
RF frequency	2855.816 MHz
Modulator HV Power Supply	4.42 (Knob Setting)
RF macro Pulse Length (FWHM)	200 ns
Peak Current on FC	37.2 mAmps
Scope on FC
e- Beam Energy	14 MeV

We did scanning with Q1. We took 7 images of each

Tune by Sadiq

Previous Tune at the higher energy

Solenoid 1	5.4 A
Solenoid 2	5.5 A
Gun Ver	-0.2 A
Gun Hor	+0.4 A
Output Hor	-0.5 A
Output Ver	-0.5 A
Gun HV	+9.75 (Knob Setting)
Gun Grid Voltage	5.25 (Knob Setting)
RF frequency	2855.813 MHz
Modulator HV Power Supply	4.11 (Knob Setting)
RF macro Pulse Length (FWHM)	200 ns

Following table shows the OTR images of beam and scope images of FC. As we see, second tuning has the smallest and the brightest beam spot. So, we chose second as our best tune.

V1 (Gun Vertical)	H1 (Gun Horizontal)	Sol1 (Gun Sol)	V2 (Output Vertical)	H2 (Output Horizontal	Sol 2 (Output Solenoid)	OTR Image	FC Scope Image
(A)	(A)	(A)	(A)	(A)	(A)
(-0.3)	+0	0	0	-0	-0
(-0.2)	+0.4	5.4	-0.5	-0.5	5.5
(-0.2)	+0.4	6.8	-0.5	-0.5	5.5
(-0.2)	+0.4	6.8	-0.5	-0.5	10.4

Data Analysis and Results on March 2011 Experiment

Calibration constants

With similar method used before, we found calibration constants for vertical and horizontal calibrations:

image	OTR image	cal_h (mm/px)	cal_v (mm/px)
		0.04308	0.04204
		0.04320	0.04228
		0.04349	0.04181
		0.04323	0.04196
		0.04337	0.04212
		mean (mm/px)	mean (mm/px)
		[math] 0.04327 \pm 0.00016 [/math]	[math] 0.04204 \pm 0.00018 [/math]

Non-Gaussian Fit for Beam

The projection of the beam is not Gaussian distribution. So, we fit Super Gaussian fitting <ref name="BeamDisBeyondRMS"> F.-J Decker, “Beam Distributions Beyond RMS”, BIW94, Vancouver,CA,Sep 1994, . </ref>.

<ref name="BeamDisBeyondRMS"></ref>

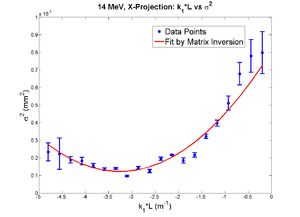
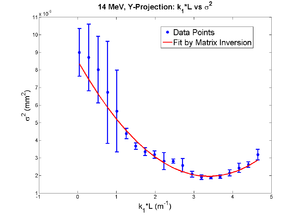
Parabola Fitting for the Sigmas

We used the MATLAB to analyze the data. The results shows that:

[math] \sigma_x^2= (3.678 \pm 0.022) + (-4.17 \pm 0.22)k_1L + (5.55 \pm 0.42)(k_1L)^2 [/math]

[math] \epsilon_x = 0.417 \pm 0.023~mm*mrad ~\Rightarrow~ \epsilon_{n,x} = 11.43 \pm 0.64~mm*mrad[/math]

[math] \beta_x=1.385 \pm 0.065, \alpha_x=0.97 \pm 0.07 [/math]

[math]\sigma_y^2 = (2.843 \pm 0.044) + (1.02 \pm 0.52)k_1L + (3.8 \pm 1.2)(k_1L)^2 [/math]

[math] \epsilon_y = 0.338 \pm 0.065~mm*mrad ~\Rightarrow~ \epsilon_{n,y} = 9.3 \pm 1.8~mm*mrad[/math]

[math] \beta_y=1.17 \pm 0.19, \alpha_y=0.22 \pm 0.10 [/math]

Positron Detection

To detect positrons created, we want a put Tungsten target at the end of 90 degree beamline. When positrons hit W-target, 511 keV photons will be created. We want to use NaI detectors to detect these 511 keV photons, so we might have an estimate on the numbers of the positrons we collect at the end of the 90 degree beamline.

We acquired some NaI crystals from Idaho Accelerator Center (IAC). We built our own PMT bases for them, since the bases we had not working properly. We modified the design of model PA-14 from Saint-Gobain crystals & detectors ltd. Following image is the design.

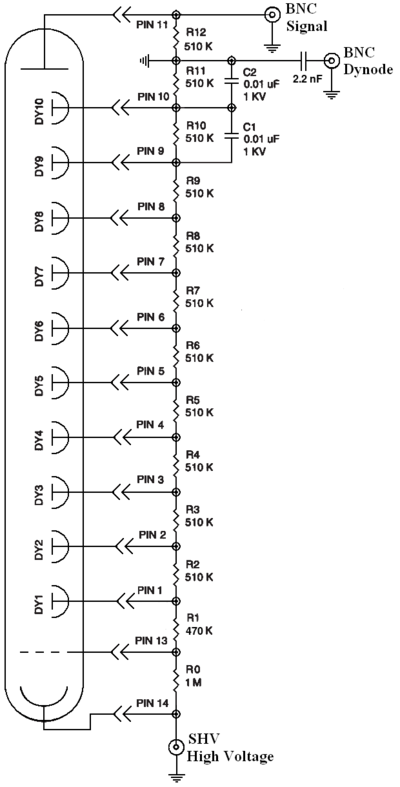Future Plan

Positron Target

A tungsten target will be placed in the space between 1st and 2nd triplet. The tungsten target will be placed inside a big chamber.

We are going to run

Emittance tests with Energy Scan

We will do emittance test with precise energy scan. We remapped dipole magnet for more precise energy scan. This will also improve our emittance measurement.

Positron Yield

We will insert the first tungsten target and create positrons. We are expecting to collect part these positrons and transport them down the second tungsten target at the end of the 90 degree beamline. By doing these, 511 keV photons will be created and we want to detect them by our NaI detectors.

References

<references/>

Appendix

File:Emittance.tex