(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
go back
Thin Absorbers
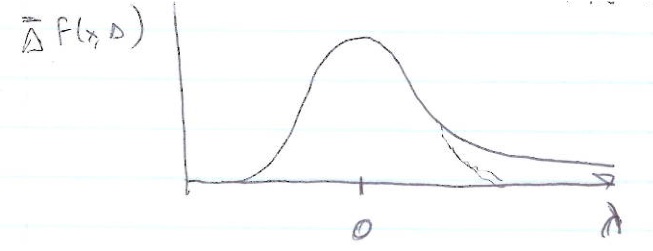
In thin absorbers the number of collisions is small preventing the use of the central limit theorem to describe the stochastic process of energy loss in terms of a Gaussian distribution. The Large energy transfers that are possible cause the energy loss distribution to look like a Gaussian one with a high energy tail (or foot).
The skewness of the resulting energy loss distribution is quantified as
- [math]\kappa = \frac{\bar{\Delta}}{W_{max}}[/math]
- [math]\Delta \equiv 2 \pi N_a r_e^2 m_e c^2 \rho \frac{Z}{A} \left ( \frac{z}{\beta}\right)^2 x [/math] = lead term in Bethe Bloch equation
[math]\rho[/math] = density of absorbing material.
- [math]W_{max} = \frac{(pc)^2}{\frac{1}{2} \left [ m_e c^2 + \left ( \frac{M^2 c^2}{m_e} \right ) \right ] + \sqrt{(pc)^2 + (Mc^2)^2}}[/math] = max energy transfered in 1 collision (headon / knock out collision)
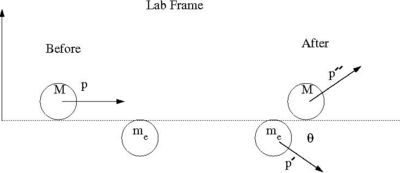
This comes from the relativistic kinematics of an Elastic Collision.
- [math]\gamma = \frac{E_{tot}}{Mc^2} = \frac{ \sqrt{(pc)^2 + (Mc^2)^2}}{Mc^2}[/math]
- [math]\beta= \frac{pc}{\gamma Mc^2} = \frac{pc}{E_{tot}}[/math]
- [math]E_k = E_{tot} - Mc^2 = \gamma Mc^2 - Mc^2 = (\gamma - 1 ) Mc^2[/math]
- [math]E_k = \sqrt{(pc)^2 + (Mc^2)^2} - Mc^2 [/math]
- [math] (p^{\prime}c)^2 = E_k^2 + 2E_km_ec^2[/math]
Conservation of Momentum [math]\Rightarrow[/math] :
- [math]\vec{p} = \vec{p}^{\; \prime \prime} + \vec{p}^{\; \prime}[/math]
Conservation of Energy [math]\Rightarrow[/math] :
- [math]E_{tot} + m_ec^2 = E_{tot}^{\prime \prime} + E_{tot}^{\prime}[/math]
- [math]\sqrt{(pc)^2 + (Mc^2)^2} + m_ec^2 = \sqrt{(p^{\; \prime \prime} c)^2 + (Mc^2)^2} + E_k + m_e c^2[/math]
using conservation of E & P as well as substituting for [math]p^{\prime}[/math] you can show
- [math](p^{\; \prime \prime}c)^2 = (pc)^2 - 2E_k\sqrt{(pc)^2 +(Mc^2)^2} + E_k^2[/math] : cons of E
- [math]= (pc)^2 + E_k^2 + 2E_km_ec^2 -2pc\sqrt{E_k^2+2E_km_ec^2} \cos(\theta)[/math] : cons of P
[math]\Rightarrow[/math]
- [math]pc \cos(\theta) \sqrt{1+\frac{2m_ec^2}{E_k}} = \sqrt{(pc)^2+(Mc^2)^2} + m_ec^2[/math]
solving for [math]E_k[/math]
- [math]E_k = \frac{2m_ec^2(pc)^2\cos^2 (\theta)}{[\sqrt{(pc)^2 + (Mc^2)^2} +m_ec^2]^2 - (pc)^2 \cos^2 (\theta)}[/math]
(Landau Theory)
[math]\kappa \leq 0.01[/math]
Landau assumed
- [math]W_{max} = \infty[/math] is max energy transfer
- electrons are free (energy transfer is so large you can neglect binding)
- incident particle maintains velocity (large momentum transfer from big mass to small mass) (bowling ball hits ping pong ball)
L. Landau, "On the Energy Loss of Fast Particles by Ionization", J. Phys., vol 8 (1944), pg 201
instead of a gaussian distribution Landau used
- [math]P(x,\Delta) \propto \frac{1}{\bar{\Delta}\pi} \int_0^{\infty} e^{-u \ln u - u \lambda} \sin(\pi u) du[/math]
where
- [math]\lambda = \frac{1}{\bar{\Delta}} \left [ \Delta - \bar{\Delta} \ln \bar{\Delta} - \ln \epsilon + 1 -C \right ][/math]
- [math]\bar{\Delta} = 2\pi N_a r_e^2 m_e c^2 \rho \frac{Zz^2}{A \beta^2}x[/math]
- [math]\ln \epsilon = \ln \left [ \frac{(1-\beta^2)I^2}{2m_ec^2 \beta^2} \right ][/math]
- [math]C = 0.577[/math]
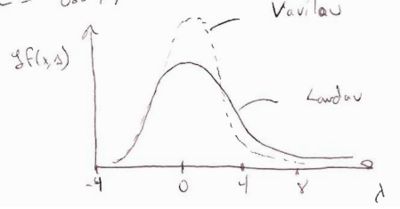
(Vavilou's Theory)
Vavilous paper
P.V. Vavilou, "Ionization losses of High Energy Heavy Particles", Soviet Physics JETP, vol 5 (1950? )pg 749
describe the physics for the case
- [math]0.01 \lt \kappa \lt \infty [/math]
The distribution function derived is shown below as well as a conceptual overlay of Vavilou's and Landau's distributions. (The [math]\zeta f(x,\Delta)[/math] in the picture should be a [math]\bar{\Delta}P(x,\Delta)[/math] )
- [math]P(x,\Delta) = \frac{1}{\bar{\Delta}\pi} x e^{x(1+\beta^2C)} \int_0^{\infty} e^{xf_1} \cos(y \lambda_1 + xf_2) dy[/math]
where
- [math]f_1 = \beta^2 \left [ \ln(y) - C_i(y)\right ] - \cos(y) - y S_i(y)[/math]
- [math]f_2 = y\left [ \ln(y) - C_i(y)\right ] + \sin(y) + \beta^2 S_i(y)[/math]
- [math]C_i(y) \equiv - \int_y^{\infty} \frac{\cos(t)}{t} dt[/math]
- [math]S_i(y) \equiv \int_0^{y} \frac{\sin(t)}{t} dt[/math]
- [math]C = 0.577[/math]